|
Geometrical aspects of Bora
Paulus Gerdes Mozambican Ethnomathematics Research
Centre, C.P. 915,
Abstract:The paper discusses some geometrical aspects of Bora basketry in the Peruvian Amazon. In particular, twill-plaited, circular trays called níjtyubane are analysed. Elements of their production and of the creation and transformation of geometric patterns are studied. An outline of their historical development is presented that stresses the similarity and the cultural diversity. Introductory remarks: Basketry, ethnomathematics and the history of mathematics. Many peoples do not appear referred to in the mathematics history books. This does not mean that these peoples do not have produced mathematical ideas. It means only that their ideas have not (as yet) been recognised, understood or analysed by professional mathematicians and historians of mathematical knowledge. In this respect the role of ethnomathematics as a research area resides in contributing with studies that permit to begin with the recognition of mathematical ideas of these peoples and to value their knowledge in diverse ways, including the use of this knowledge as starting base in mathematics education. Having ethnomathematics been born in Brazil with the reflections of Ubiratan D’Ambrosio, I feel honoured by the invitation of the editor Sérgio Nobre to contribute to the Brazilian Journal for the History of Mathematics with a historic-ethnomathematic theme. A fertile area for the symmetric-geometric exploration was, in many cultures ‘forgotten’ in the mathematics history books, the conception and production of twill-woven mats and baskets. At the end of the paper I will make a brief reference to the ethnomathematical studies ‘avant la lettre’ at the beginning of the 20th century of Brazilian twill-plaited objects by Max Schmidt. In various studies I tried to contribute to the understanding of forms of geometrical thinking involved in the production of plaited objects. For example in the paper (Gerdes 1989), I analyse some aspects of arithmetic and geometrical ornamentation of baskets from the Brazilian Amazon. In the books (Gerdes & Bulafo 1994, Gerdes 2003a) strip patterns woven into handbags by Tonga women in the Southeast of Mozambique are studied. In the papers (Gerdes 2000b, 2004) mats woven by Yombe women from the Lower-Congo area are analysed (cf. Gerdes 1999, pp. 126-137). In the paper (Gerdes 2002a) I present a comparative analysis of twill-woven octagons produced on mats and baskets from various parts of the world. Recently concluded are, among others, a book on geometry and basketry in the Makhuwa culture of Northeast Mozambique (cf. Gerdes 2003b), an analysis of Kongo baskets from the 17th century and a comparative study of woven concentric toothed squares and of plane patterns composed of sets of concentric toothed squares. My colleague Marcos Cherinda (2002) concluded a doctoral thesis on the exploration of plaited patterns in mathematics education using a weaving-board. In the book The circle and the
Square: Geometric, Artistic and Symbolic Creativity of Basket Weavers from
Africa, America, Asia and Oceania (Gerdes, 2000a)
I present a comparative study of basket-trays with a circular rim and a
twill woven bottom. In three chapters cultures of South America are analysed,
the Warao (Venezuela / Guyana, pp. 177-186), the Desana (Colombia / Brazil,
pp. 187-196) and the Yekuana (Venezuela, pp. 197-218). The book had been
concluded before knowing baskets of the same type, called níjtyubane
(Singular: níjtyuba), produced by Bora basket weavers
in the Peruvian Amazon. Photograph 1 displays an example
of a níjtyuba; its design has a rotational symmetry.
Workshop on ethnomathematics in the Peruvian Amazon At the invitation of the Training Programme for Bilingual Teachers (Programa de Formación de Maestros Bilingues, PFMB) under the joint responsibility of the State Higher Pedagogical Institute (Instituto Superior Pedagógico Público) of Loreto and the Interethnic Association for the Development of the Peruvian Jungle (Associación Interétnica de Desarrollo de la Selva Peruana, AIDESEP), I had the unique opportunity (May-June 2000) to conduct a workshop on ethnomathematics that took place in Zungarococha near Iquitos, the capital of Loreto — the Peruvian Amazon. Mathematics teachers and lecturers, linguists and teachers of various indigenous languages, indigenous teachers, anthropologists, teacher educators and several members of the Bilingual Education Unit of the Ministry of Education took part in the workshop. In order to turn the seminar more interesting, stimulating and dynamic and to concretize the presentation of ethnomathematics research methods, I tried to include examples from Amazonian cultures. The participants were invited to contribute with suggestions for themes for the seminar, completed by my recommendations, some of which were related to the analysis of objects that I had seen in Iquitos. During the workshop two periods of four hours were dedicated to the analysis of Bora baskets. In the first period, the teacher of the Bora language, Gerardo del Aguila Mibeco, presented a brief introduction to the history and culture of the Bora and explained some aspects of the production of níjtyubane basket trays. Thereafter the participants tried to produce a Bora mat and basket and to reflect, at each step of the production process, about the embedded geometric-mathematical ideas. An exchange of observations took place and possibilities for an exploration in mathematics education were discussed. During my stay in Iquitos I acquired
twelve níjtyubane and was able to photograph 19 others at
shops and at the San Juan market and three more in Zungarococha. These
34 níjtyubane constitute the basis for the analysis to be
presented. The following text is an extract of a more extended and detailed
analysis prepared for inclusion in the book
Geometry and Basketry of
the Bora in the Peruvian Amazon (Gerdes 2003f).
About the Bora Little written information is available about the Bora. They live along the upper Cahuinari and the Igara-Paraná rivers in the Colombian and Peruvian Amazon (cf. the maps in Queixalós & Renault-Lescure, 2000). The denomination "Bora" derives from "irapora", a Tupi designation meaning "honey people". According to the legend, the Cahuinari had been created by the fall of the cosmic tree at which the different groups were housed. The Bora had been living near the top of the tree like the bees. The Bora call themselves Mé Múiná, i.e., "Human beings " (Tamisier, p. 57). Originally from Colombia, the Bora people were still at the beginning of the 20th century about 12 thousand (Tessmann, p. 267). The population census of 1993 counted 371 Bora, probably an underestimation (Brack, p. 63). Today the Bora are estimated to be around 2000 people (Tamisier, p. 56; oral information of Mibeco, 2000). Dispersed in the dense forest, the Bora live usually in small autonomous communities of 50 to 200 people (Forde, p. 143). They live basically from agriculture, hunting and fishing, being cassava the main agricultural crop. Figure 1 illustrates a big communal house called ‘maloca.’ During the seminar in Zungarococha, the Bora teacher Gerardo Mibeco explained how the posts of a ‘maloca’ are marked on the ground: after starting with a central square, an octagonal structure is marked on the floor (see Figure 2).
Considerations of a geometrical nature appear in various cultural activities. For instance, the Bora decorate fruits, wood and ceramics; tattoo their bodies. Both women and men weave mats and baskets with strips of various colours, producing complex decorative patterns (cf. Forde, p. 138-142). I did not encounter studies about
Bora artisanship or about the knowledge crystallised in their crafts.
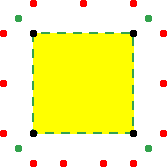
Production process of níjtyubane Essentially the production of níjtyubane is not very different from the production of circular plaited trays and baskets as analysed in the book The Circle and the Square (Gerdes, 2000a). The Bora basket weavers who produce níjtyubane are generally men. Women use níjtyubane as a winnowing tray or a plate for serving or drying food. To produce a níjtyuba, a basket weaver begins with weaving a square mat. He takes two flexible branches (diameter 6 to 14 mm) of more or less the same length; bends each of them in an arc and fastens the extremes to each other. In this way he obtains two circular rims of almost equal diameters. He wets the mat, fastens the strips in between the two circular rims and cuts off the outstanding strip parts. To weave the bottom of a níjtyuba strips of more or less the same width are used (3 to 6 mm depending on the case) of the bájyuhba plant (bombonaje in Spanish). The natural colour of one face of the strips is dark brown, whereas the other face is yellow. When one scrapes the brown face of a strip it becomes yellow too. Frequently Bora artisans weave a mat in such a way that in one direction scraped strips and in the other natural strips are used. In this way yellow–brown patterns appear on the interior face of the níjtyuba. The exterior face that is constituted by the backsides of the strips is of only one colour: yellow. To guarantee a good balance of the final product it is important that the initial mat is really square. To achieve this the Bora artisan weaves the mat in such a way that the middle lines of the sides of the square become visible (Figure 3a): he starts the weaving near to the future mat centre, called tujkénu. He guarantees, in general, that the middle lines become visible from the start of weaving process onwards. The visible middle lines of the mat are transformed into two visible axes of the níjtyuba, like the diagram in Figure 3b illustrates.
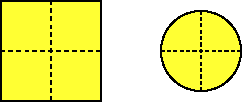
The proportion between the length of the side of the square mat and the circular rim determines the height of the níjtyuba. Figure 4 displays possible transversal images in function of this proportion.
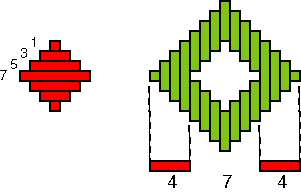
‘Butterflies’ formed by concentric toothed squares In the majority of the níjtyubane appears a type of design, called ‘butterflies’ by the Bora basket weavers. The ‘butterflies’ are composed of concentric toothed squares. Figure 5 presents in isolation a ‘butterfly’ woven into a níjtyuba. This ‘butterfly’ is composed of
two toothed squares (see Figure 6). The central square
has a diameter of seven units. This means that the central horizontal strip
passes above seven vertical strips. The second toothed square is a ‘ring’
around the central toothed square. The central horizontal strip passes
now under four vertical strips.
We may say that this ‘butterfly’ is characterised by three numbers, namely the dimension of the centre (=7), the number of concentric toothed squares (=2) and the number of strips under which the central horizontal strip passes when leaving the central square (=4). In general ‘butterflies’ of the considered type are characterised by a triple of numbers (D, N, W), where D represents the dimension of the central toothed square, N the number of concentric toothed squares and W the width of the consecutive rings. The Bora artisans are very creative in inventing distinct ‘butterflies.’ On the níjtyubane trays that I had the opportunity to analyse, I found 26 distinct ‘butterflies’ – a number higher than the number of variants found so far in other cultures (see the scheme in Gerdes 2000, p. 292). The 26 distinct ‘butterflies’ are
characterised by the following triples:
The ‘butterflies’ on the níjtyuba in Photograph 2 are of the type (7, 4, 4).
Plane patterns composed of ‘butterflies’ Rarely only one ‘butterfly’ appears on a níjtyuba. Normally various ‘butterflies’ are interwoven next to each other. Frequently, all ‘butterflies’ are congruent and are positioned in the same way. Consider the ‘butterfly’ characterised by the triple (1, 2, 3). Four ‘butterflies’ of this type may be joined in various ways. Figure 7 displays three possibilities.
In the first case, the horizontal distance between two ‘butterflies’ that are horizontally neighbours is three units, whereas the vertical distance between two ‘butterflies’ that are vertically neighbours is one unit. In the second case, these distances are five and one, and in the third case 3 and 3 respectively. The three distinct situations may be characterised by the quadruple expressions (1, 2, 3, 3x1), (1, 2, 3, 5×1) and (1, 2, 3, 3×3) respectively. In general we may characterize a plane pattern of juxtaposed ‘butterflies’ by a quadruple (D, N, W, p × q), where (D, N, W) represents a repeated ‘butterfly’ and p and q the horizontal and vertical distances between the horizontally or vertically neighbouring ‘butterflies.’ When one observes a pattern (D, N, W, p × q) from another angle, the pattern appears to be the pattern (D, N, W, q × p). In this sense the patterns (D, N, W, p × q) and (D, N, W, q × p) are equivalent. Photographs 3, 4 and 5 present níjtyubane that display the twill-plaited plane patterns (1, 4, 4, 7×1), (1, 5, 3, 5×1), and (7, 4, 3, 5×1), respectively.
On the níjtyubane
observed by me, I found twenty plane patterns composed of congruent ‘butterflies.’
This constitutes an expression of the creativity and the geometric imagination
of the Bora basket weavers. The patterns are characterised by the following
quadruples:
The majority of these plane patterns of ‘butterflies’ I have not encountered so far in other cultures. As yet I observed only three of these patterns in mats or baskets plaited by artisans of other peoples. The pattern (1, 2, 2, 3×1) may be seen on a mat woven by a Yombe woman from the Lower Congo area (Central Africa). The mat is kept at the Royal Museum for Central Africa, Tervuren, Belgium, No. 80.12.30. The pattern (3, 2, 3, 5×1) is used both in the Obamba culture of Gabon (Central Africa) and by Yekuana basket weavers in Venezuela and by Cherokee basket weavers in the Southeast of the United States of America. Finally, the pattern (3, 4, 3, 5×1) appears in the Desana culture of the Colombian and Brazilian Northwest Amazon (see photographs in Perrois, p. 44; Wilbert, p. 148; Duggan, p. 17 and Hill, p. 245; and Reichel-Dolmatoff, p. 60, respectively). All patterns of the type (D, N, W, p × q) present horizontal and vertical symmetry axes. If p is equal to q, however, as is verified in the case of the Bora pattern (3, 4, 3, 3×3), the visual impression has also diagonal symmetry axes (see Figure 8).
Plane patterns composed of combinations of ‘butterflies’ The níjtyuba in Photograph 6 is covered by a single plane pattern, where strings of ‘butterflies’ of the type (3, 2, 3, 1×5) are alternated by bands of ‘butterflies’ of the same type (see Figure 9). In the transition from strips to bands the colours of the ‘butterflies’ are inverted. Another example of colour inversion may be observed on a níjtyuba of which the central band is composed of by a vertical string of ‘butterflies’ characterised by the expression (1, 4, 4, 1×7): going from one string to the next the colours are inverted (see Figure 10).
More complex plane patterns Figure 11 presents schematically the plane patterns observed in two níjtyubane (see Photographs 7 and 8). Figures 12 and 13 illustrate parts of the twill-woven patterns. The two plane patterns display different symmetries. They constitute examples of the construction of more complex plane patterns by Bora basket weavers on the basis of simpler units formed by ‘butterflies.’
Colour transformation of plaiting patterns Photograph 9 presents a special níjtyuba. Its decoration is very different from those analysed so far. In the níjtyubane analysed before, the interior face is characterised by the use of brown strips in one direction and scraped-yellow strips in the direction perpendicular to the first. In the case of the níjtyuba in Photograph 9, however, the situation is different: in both directions brown strips and scraped strips are used. More precisely brown and yellow strips are alternating in both directions.
Figure 14 presents the plane pattern formed by the horizontal strings of ‘butterflies’ of the type (1, 2, 3, 5×1) separated by zigzags with the width of three units. Figures 15 and 16 present the two distinct possibilities to transform this pattern of ‘butterfly’ strips, alternating yellow and brown strips in both directions. Figure 17 illustrates the visual impression of the first pattern that corresponds to the níjtyuba presented in Photograph 2.
This is only one example where Bora basket weavers create new images by the alternation of yellow and brown strips in both directions. Photograph 10 presents another example. More examples are presented in (Gerdes 2003f).
Historical development: Similarity and cultural diversity In several continents male and female artisans have produced basket trays with a circular rim and a twill-plaited bottom. The history of the discovery and invention of twill-plaited circular basket trays, like the níjtyubane, may be summarised as follows (Gerdes 2000a, cf. Gerdes 1990, 1992, 2003f): * Craft people conceived the idea to fasten a mat to a circular border. * They learned that a square mat is more advantageous than other rectangular mats in order to be able to produce a well-balanced basket. * Artisans discovered that it is easier to fasten a plaited square mat to the circular border if they turn the middle lines of the square visible in one way or another (Figure 3a). * One way to turn a middle line visible is by the introduction of a discontinuity line in the plaiting texture (Figure 18 presents an example). * On the intersection of discontinuity lines appear automatically ‘butterflies,’ that is, sets of concentric toothed squares or crossings in the form of an X (see the example in Figure 19). * Structures with one or two discontinuity lines may be substituted by more complex weaving structures resulting from the introduction of more discontinuity lines or by the variation of the colours of the strips. * Abstracting from the importance of the perpendicular middle lines, the geometric forms of Figure 3 may gain value on their own and being transposed to other cultural contexts; the same may happen with the more complex patterns. * The discovery of the importance of perpendicular middle lines reflects the understanding that it will facilitate the fabrication of the circular basket tray. * Once understood this importance, the realisation may vary from one culture to another and from one period to another, discovering various structures of sets of concentric toothed squares and structures with the shape of an X. * More cultural variability emerges in the following phases of the introduction of more complex designs and the transposition to other cultural contexts, resulting from the greater freedom conquered by the artisans. * Even in the phase of elaborating more complex designs, there may occur striking parallel developments such as the introduction of plaited spirals in 11th century Arizona by Anasazi basket weavers and by 19th - 20th century Makhuwa basket weavers in the Northeast of Mozambique (Gerdes 2000). 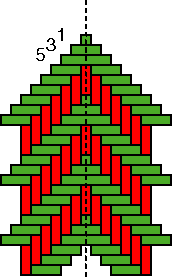
The discovery and the development
of circular basket trays exemplify a more general process of similarity
and diversity in geometric exploration, particularly in early cultural
contexts.
Final considerations The author would like to express his hope that this paper and the book (Gerdes 2003e) may serve as a stimulating starting point for the historiography of geometrical thought among the Bora. The PFMB and AIDESEP team, headed by the mathematician Dubner Medina Tuesta, had already advanced with the analysis of Bora numeration and with the elaboration of the first mathematics school books in the Bora language. Both activities mark a crucial step in the history of the Bora people, struggling arduously for its survival. A profound reflection on a consequent praxis of mathematics education, in the context of the struggle for survival of an Amerindian people in Brazil, may be found in the manuscript "Teaching mathematics and indigenous science or how I learned from the Tuyuka people" (Bazin 2001). It is hoped that this paper may stimulate the study, in Brazil and elsewhere, of baskets with a circular rim and twill-woven bottom. The ethnography of the Wayana baskets (Velthem 1998) presents a lot of material that invites to a historic-ethnomathematical reflection and field work. Ricardo (2000) gives information about Baniwa basketry, including some twill-weaving patterns and about two types of woven circular basket-trays, the waláya and the dopítsi. Among the Baniwa the design composed of concentric toothed squares is the first design each child learns. Probably the first studies, in the
Brazilian context, in which possible reasons for the appearance of concentric
toothed squares in basketry are discussed, are those of Max Schmidt. In
(Schmidt 1905, pp. 330-403 [Brazilian translation 1942])
the concept of a ‘woven quadrangle’ [German:
Geflechtsviereck] was
introduced. He speaks about the mathematical properties of these quadrangles
and studies the transposition of weaving patterns to other ornamentation
contexts (cf. Schmidt 1904,
1926).
In his autobiography Schmidt stresses that he had demonstrated that the
origin of the majority of geometrical ornaments of the South American natives
derive from the twill-weaving technique (Schmidt 1955,
p. 120). I would like to suggest a historical study of the ethnomathematical
aspects ‘avant la lettre’ of the work of Max Schmidt.
References Brack Egg, António & Yáñez, Carlos (Eds.) (1995), Amazonia peruana. Comunidades Indígenas, Conocimientos y Tierras tituladas. Atlas y base de datos, GEF / PNUD / UNOPS, Lima. Bora: pp. 62-69 Cherinda, Marcos (2002), The use of a cultural activity in the teaching and learning of mathematics: The exploration of twill weaving in Mozambican classrooms, Unpublished doctoral thesis, University of Witwatersrand, Johannesburg Duggan, Betty J. & Riggs, Brett H (1991), Studies in Cherokee Basketry with a Reprint of ‘Decorative Art and basketry of the Cherokee’ by Frank G. Speck, The Frank H. McClung Museum, The University of Tennessee, Knoxville Forde, C. Daryll (1934), The Boro of the Western Amazon Forest, in: C. Daryll Forde, Habitat, Economy and Society. A Geographical Introduction to Ethnology, Dutton, New York, pp. 131-147, 479 Gerdes, Paulus (1989), Sobre aritmética e ornamentação geométrica. Análise de alguns cestos de índios do Brasil, BOLEMA Especial, Universidade Estadual Paulista, Rio Claro, 1989, No. 1, 11-34; reproduced in: QUIPU: Revista Latinoamericana de Historia de las Ciencias y la Tecnología, Mexico City, 1989, Vol. 6, 171-187, and in: Mariana Leal Ferreira (Ed.), Ideias Matemáticas de Povos Culturalmente Distintos, Global Editora, São Paulo, 2002, 206-220. Gerdes, Paulus (1990), Ethnogeometrie. Kulturanthropologische Beiträge zur Genese und Didaktik der Geometrie, Verlag Franzbecker, Bad Salzdetfurth (2nd edition 2002) (Preface by Peter Damerow) Gerdes, Paulus (1992), Sobre o despertar do pensamento geométrico, Universidade Federal de Paraná, Curitiba (2nd edition 2003) (Preface by Ubiratan D’Ambrosio). Gerdes, Paulus (1999), Geometry from Africa: Mathematical and Educational Explorations, The Mathematical Association of America, Washington DC (Preface by Arthur B. Powell). Gerdes, Paulus (2000a), Le cercle et le carré: Créativité géométrique, artistique, et symbolique de vannières et vanniers d’Afrique, d’Amérique, d’Asie et d’Océanie, L’Harmattan, Paris (Preface by Maurice Bazin). Gerdes, Paulus (2000b), Gerade und Ungerade – Zu einigen mathematischen Aspekten der Mattenflechterei der Yombe-Frauen am unteren Kongo, em: Jürgen Blankenagel & Wolfgang Spiegel (Ed.), Mathematikdidaktik aus Begeisterung für die Mathematik. Festschrift für Harald Scheid, Ernst Klatt Verlag, Stuttgart, 83-93. Gerdes, Paulus (2002a), Twill-Plaited Octagonal Designs, Visual Mathematics, 4(3) [available online at: http://members.tripod.com/vismath/pap.htm by going to issue 4(3)] Gerdes, Paulus (2003a), Sipatsi: Cestaria e Geometria na Cultura Tonga de Inhambane, Moçambique Editora, Maputo, 176 p. Gerdes, Paulus (2003b), Symmetry-Geometry Aspects of Mavuku Baskets among the Makhuwa (Mozambique), Symmetry: Culture and Science, Budapest, 12(1-2), 87-114 (to be reproduced in Visual Mathematics [available online at: http://members.tripod.com/vismath/pap.htm]). Gerdes, Paulus (2003c), Exploring Plaited Plane Patterns among the Tonga in Inhambane (Mozambique), Symmetry: Culture and Science, Budapest, 12(1-2), 115-126 (to be reproduced in Visual Mathematics [available online at: http://members.tripod.com/vismath/pap.htm]). Gerdes, Paulus (2003d), Plaited strip patterns on Tonga handbags in Inhambane (Mozambique) – An update, Visual Mathematics, 5(1) [available online at: http://members.tripod.com/vismath/pap.htm] Gerdes, Paulus (2003e), Geometria y Cestaria de los Bora en la Amazonia peruana, Iquitos (in press) Gerdes, Paulus (2003f), Awakening of Geometrical Thought in Early Culture, MEP Press, Minneapolis MN (Preface by Dirk Struik). Gerdes, Paulus (2004), Symmetries on mats woven by Yombe women from the Lower Congo area: On the interplay between cultural values and mathematical-technical possibilities, in: Dorothy Washburn & Donald Crowe (Eds.), Symmetry Comes of Age, The Role of Pattern in Culture, University of Washington Press, Seattle, 81-99. Gerdes, Paulus & Bulafo, Gildo (1994), Sipatsi:Technology, Art and Geometry in Inhambane, Universidade Pedagógica, Maputo Hill, Sarah H. (1997), Weaving New Worlds: Southeastern Cherokee Women and their Basketry, The University of North Carolina Press, Chapel Hill Perrois, Louis (Ed.) (1969), Gabon: Cultures et Techniques, ORSTOM, Libreville Queixalós, Francisco & O. Renault-Lescure (Eds.) (2000), As línguas amazônicas hoje, Instituto Socioambiental, São Paulo Reichel-Dolmatoff, Gerardo (1985), Basketry as metaphor: Arts and crafts of the Desana indians of the Northwest Amazon, University of California Museum of Cultural History, Los Angeles Ribeiro, Berta (1985), A arte do trançado dos índios do Brasil, um estudo taxonômico, Museu Paranense Emílio Goeldi, Belém Ricardo, Beto (Eds.) (2000), Arte Baniwa, Federação das Organizações Indígenas do Rio Negro, São Gabriel da Cochoeira AM [available on-line at: www.socioambiental.org/website/baniwa/index.htm] Schmidt, Max (1904), Ableitung südamerikanischer Geflechtmuster aus der Technik des Flechtens, Zeitschrift für Ethnologie, 34, 490-512 Schmidt, Max (1905), Indianerstudien in Zentralbrasilien. Erlebnisse und ethnologische Ergebnisse einer Reise in den Jahren 1900 bis 1901, Dietrich Reimer, Berlin Schmidt, Max (1926), Die technischen Voraussetzungen in der Ornamentik der Eingeborenen Südamerikas, Jahrbuch für Prähistorische und Ethnografische Kunst, II, 142-174 Schmidt, Max (1942), Estudos de Etnologia Brasileira, Peripécias de uma viagem entre 1900 e 1901. Seus resultados etnológicos, Companhia Editora Nacional, São Paulo Schmidt, Max (1955), Autobiografia de Max Schmidt, Revista de Antropologia, São Paulo. 3, 115-124 Tamisier, Jean-Christophe (Ed.) (1998), Dictionaire des Peuples, Sociétés d’Afrique, d’Amérique, d’Asie et d’Océanie, Larousse, Paris. Bora: pp. 56-57 Tessmann, Günther (1930), Bora, in: G. Tessmann, Die Indianer Nordost-Perus. Grundlegende Forschungen fuer eine systematische Kulturkunde. Hamburg: Friedrichsen, 267-280 Velthem, Lúcia Hussak van (1998), A pele de Tuluperê, uma etnografia dos trançados Wayana, Museu Paraense Emílio Goeldi, Belém Wilbert, Johannes (1972), Survivors of Eldorado: Four Indian Cultures of South America, Praeger New York
|