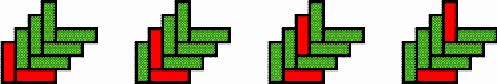|
Exploring plaited plane patterns among the Tonga in
Inhambane (Mozambique)
Paulus Gerdes Mozambican Ethnomathematics Research Centre, C.P. 915,
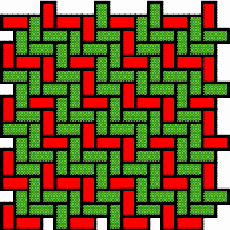
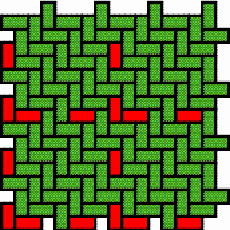
Gitonga is one of the languages spoken in the Inhambane province in Southeast Mozambique. It is the main language of the population living in the coastal districts of Inhambane, Jangamo, Maxixe and Morrumbene. Gitonga is the mother tongue of about 170.000 people. Because of their beauty and utility, baskets made by Tonga weavers, who are mostly women, are among the most appreciated products of Mozambican craftwork. The baskets of the highest quality and with most variation in their design are produced on the peninsula of Linga-Linga, almost only reachable by boat. The peninsula lies in the district of Morrumbene, about 500 km to the Northeast of the country’s capital Maputo. Some baskets are commercialised at nearby markets but others find their way directly to the markets of Maputo. The books (Gerdes & Bulafo 1994) and (Gerdes 2003a) analyse Tonga handbags called gipatsi (Plural: sipatsi). To produce these handbags the artisans use as basic weave the ‘over two, under two’ twill (notation: 2/2). By introducing some systematic changes in the weave along bands of the texture, they create attractive strip patterns (for an introduction see Gerdes 1998, chapter 1 or Gerdes 1999, pp. 87, 140-143). Photograph 1 presents an example of a gipatsi. In one weaving direction all the strands are coloured, while in the opposite direction all strands maintain their natural colour. In the last years the strip patterns found their way to other plaited objects like hats and larger bags. The Tonga weavers are very creative in inventing new strip patterns. A catalogue of 362 different strip patterns has been included in (Gerdes 2003a). An update was published in Visual Mathematics (Gerdes 2003b). Recently Tonga basket weavers created an interesting series of plane patterns. These patterns are not the result of changes in the weaving. Throughout (large parts of) the texture the twill remains the same. This time the ‘over three, under three’ twill (3/3) is the most common. The patterns, on the contrary, are produced by the use in both weaving directions of groups of n strands whereby one strand is coloured and the other n-1 strands maintain their natural colour. In both weaving directions, the plane patterns have the same periodicity (period = n). We will use the notation [m/m, n] to indicate the class of plane patterns, for which the m/m twill is used and that have period n. If only one pattern belongs to the class, we will use the notation [m/m, n] also to indicate the pattern; else the patterns will be indicated successively by [m/m, n] 1, [m/m, n] 2, etc. Figure 1 presents an example. The basic weave is the 2/2 twill. The coloured and natural strands alternate in both directions (n=2), creating a zigzag pattern. A basic weaving unit of period 2 is repeated (see Figure 2). Photograph 2 displays a handbag with three bands on which this plane pattern has been materialised. Figures 3 to 12 present the plaiting texture and visual image of plane patterns invented by Tonga basket weavers and materialised on the bags displayed in Photographs 3 to 9. Sometimes the basket weaver is able to interweave two different plane patterns into the same bag. Note that the figures represent the two weaving directions as horizontal and vertical, whereas on the photographs they make angles of 45 degrees with the horizontal line. The plane pattern in Figure 7 belongs to the [3/3, 4] class. A basic weaving unit of period 4 is repeated (Figure 13). We may ask how many different plane patterns belong to the considered class. At first sight one might think that the number of distinct patterns [3/3, 4] is equal to 4. There exist 4 possibilities to introduce a coloured strand in the vertical direction after having selected a coloured strand for the first horizontal strand of its basic weaving unit (see Figure 14). Figure 15 presents (the visual image of) the respective plane patterns that the four basic weaving units generate. They are very similar. The first one can be transformed into the second by a rotation of 90 degrees followed by a reflection; the third can be transformed into the first by a translation, etc. The four patterns may be considered instances of the same plane pattern. In general, two plane patterns are considered instances of the same plane pattern if one can be transformed into the other by a (sequence of) rotation(s), translation(s), and/or reflection(s). Only one plane pattern belongs to the class [3/3, 4]. Table 1 displays the number of distinct
plane patterns belonging to the [m/m, n] classes observed on Tonga baskets
presented above.
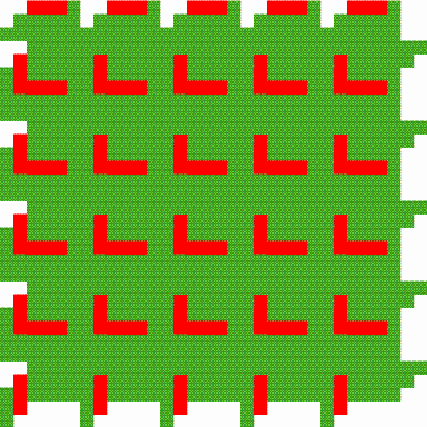
Table 1 The reader is invited to verify that there exist no more plane patterns belonging to the classes [m/m, n] for the values m and n considered in Table 1, than the ones realised on the Tonga baskets presented in the Photographs. In other words, Tonga basket weavers found all possibilities for the values of m and n considered. The baskets with these plane patterns appeared for the first time and in the same period (June-September 2002) on the central market in Maputo. The same techniques, the same material and the same colours are used to produce them. I have the impression that we are dealing with the creative imagination of one basket weaver or of a small group of basket weavers. Unfortunately, the variation in patterns will hardly be noticed by most potential buyers and so far adds (little or) nothing to their commercial value. The invention of the plane patterns responds, however, to the intellectual, geometric and artistic pursuit of their creator(s), attracting the natural attention of other mathematicians. Another special basket reinforces our conclusion (see Photograph 10). The basket weaver uses exceptionally a less balanced twill, in one direction "over two, under three" and consequently "under two, over three" in the other direction. It is the 2/3 twill (Figure 16). The artisan opted for period 5: in both directions, four natural strands follow each time after one coloured strand (Figure 17). The option for the 2/3 twill enabled the weaver to produce a plane pattern with L’s that has an axial symmetry. This would have been impossible if the basket weaver would have used a balanced m/m twill. The selection of the 2/3 twill was not at all haphazard, but resulted from a careful, rational analysis and it reflects a particular interest of its inventor in symmetry. Table 2 presents the symmetry classes
to which the Tonga plane patterns belong, using the international notation
(see Crowe and Washburn, p. 128). It may be interesting
and enriching to try to know how the inventors of the plane patterns see
or describe the symmetries of their patterns.
Table 2
Photograph 1: Example of a Tonga handbag with strip patterns
Photograph 2: Bag with bands of the
[2/2, 2] pattern
Photograph 3: Small handbag with the
[2/2, 3] pattern
Photograph 4: Handbag with the [3/3,3] 1
Photograph 5: Handbag with the [3/3, 4] pattern
Photograph 6: Bag with the [3/3, 5] pattern
Photograph 7: Handbag with the two [3/3, 6] patterns
Photograph 8: Bag with the two [4/4, 4] patterns
Photograph 9: Bag decorated partially with the [2/2, 8]
pattern
Figure 4: Pattern [2/2, 8]
Figure 5: Pattern [3/3, 3] 1
Figure 6: Pattern [3/3, 3] 2
Figure 8: Pattern [3/3, 5]
Figure 9: Pattern [3/3, 6] 1
Figure 10: Pattern [3/3, 6] 2
Figure 11: Pattern [4/4, 4] 1
Figure 12: Pattern [4/4, 4] 2
Figure 13: 3/3 Basic weaving unit of
period 4
Figure 15: Visual images of the patterns
generated by the four possible basic weaving units
References Gerdes, Paulus (1998) Women, Art and Geometry in Southern Africa, Lawrenceville NJ: Africa World Press ___ (1999) Geometry from Africa: Mathematical and Educational Explorations, Washington DC: The Mathematical Association of America ___ (2003a) Sipatsi: Cestaria e Geometria na Cultura Tonga de Inhambane, Maputo: Moçambique Editora ___ (2003b) Plaited strip patterns
on Tonga handbags in Inhambane (Mozambique) – An update, Visual Mathematics,
Belgrade, March 2003, Vol. 5, No. 1
Gerdes, Paulus and Bulafo, Gildo (1994)
Sipatsi:
Technology, Art and Geometry in Inhambane, Maputo: Universidade Pedagógica
|