

Next: Untwisted Symmetry Groups
Up: Symmetries of Columns
Previous: Symmetries of Columns
In this section, we classify the closed subgroups of
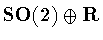 up to scaling
and conjugacy in
up to scaling
and conjugacy in 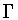 .
Also, we compute the normalizers of these subgroups in .
Also, we compute the normalizers of these subgroups in 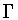 . .
Lemma 2.1
Suppose that C is a compact subgroup of
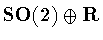 .
Then
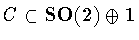 .
Proof:
If
 and
and 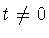 ,
then ,
then
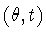 generates a noncompact subgroup of
generates a noncompact subgroup of
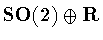 (isomorphic to
(isomorphic to
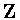 ). It follows that ). It follows that
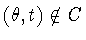 . .
Proposition 2.2
Suppose that G is a closed connected
subgroup of
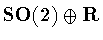 .
Then, up to conjugacy and scaling, G is one of the
subgroups
where
Proof: If
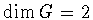 ,
then connectivity implies that ,
then connectivity implies that
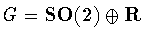 .
If .
If 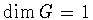 ,
then connectivity implies that G is group isomorphic to either ,
then connectivity implies that G is group isomorphic to either
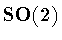 or
or
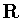 .
In the first case, it follows from Lemma 2.1 that .
In the first case, it follows from Lemma 2.1 that
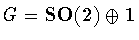 .
In the second case, there is a smooth isomorphism .
In the second case, there is a smooth isomorphism
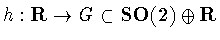 .
This isomorphism is given by .
This isomorphism is given by
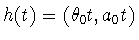 for some
for some
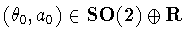 (defined as h(1)).
By assumption
(defined as h(1)).
By assumption 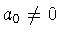 .
If .
If
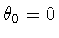 ,
then ,
then
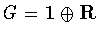 .
If .
If
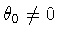 ,
then by axial scaling we can arrange that ,
then by axial scaling we can arrange that
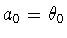 and
and 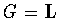 . .
>From now on, we use the abbreviations
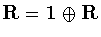 and
and
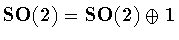 .
The proper closed subgroups of .
The proper closed subgroups of
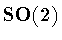 are given by
are given by 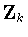 , ,
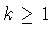 :
the subgroup of rotations of the
cylinder through angles which are multiples of :
the subgroup of rotations of the
cylinder through angles which are multiples of 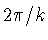 .
In addition,
we set .
In addition,
we set
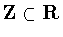 to be the subgroup of unit axial translations of the
cylinder generated by the element
to be the subgroup of unit axial translations of the
cylinder generated by the element
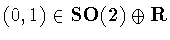 .
Finally, for any .
Finally, for any
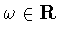 ,
we define ,
we define
Of course,
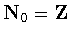 . .
Theorem 2.3
Up to axial scaling and conjugacy, the closed
subgroups
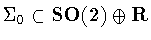
are listed in Table 1.
Table:
Classification of closed subgroups
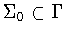 up to
scaling and conjugacy. The normalizers are given by
up to
scaling and conjugacy. The normalizers are given by
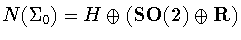
 |
Proof:
Since 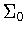 is abelian, we can write
is abelian, we can write
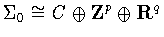 where C is compact and
where C is compact and 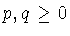 .
Clearly, .
Clearly, 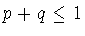 .
By
Lemma 2.1, .
By
Lemma 2.1,
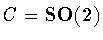 or
or
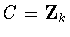 . .
Assume that
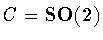 .
Since .
Since
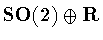 is connected, the only subgroup
satisfying
is connected, the only subgroup
satisfying
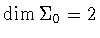 is
is
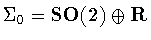 .
Suppose next that .
Suppose next that
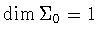 .
We claim that .
We claim that
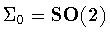 or
or
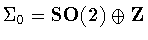 .
Choose the smallest positive .
Choose the smallest positive
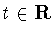 such that there is
such that there is
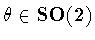 with
with
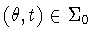 .
Since .
Since
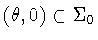 ,
it follows
that ,
it follows
that
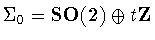 ,
where ,
where 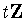 is the subgroup of
is the subgroup of
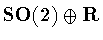 generated by (0,t). By making an axial scaling, we can set t=1 so that
generated by (0,t). By making an axial scaling, we can set t=1 so that
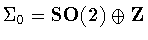 . .
Now assume that
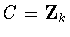 .
If .
If
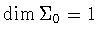 ,
then it follows from
Proposition 2.2 that ,
then it follows from
Proposition 2.2 that
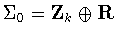 or
or
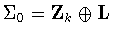 .
If .
If
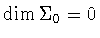 ,
then either ,
then either
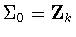 or
or
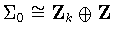 .
In the latter
case, we can choose a generator .
In the latter
case, we can choose a generator
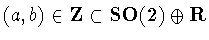 with smallest b>0.
Making an axial scaling, we can suppose that the generator is of the form
with smallest b>0.
Making an axial scaling, we can suppose that the generator is of the form
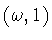 for some
for some
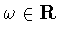 .
In other words, .
In other words,
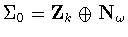 .
Note that .
Note that
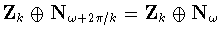 ,
so we can suppose that ,
so we can suppose that
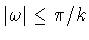 .
Using formula (2.1) we compute that .
Using formula (2.1) we compute that
where
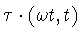 is an abbreviation for
is an abbreviation for
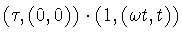 .
Hence up to conjugacy, we may suppose
that .
Hence up to conjugacy, we may suppose
that
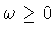 .
The case .
The case 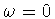 is the distinguished case
is the distinguished case
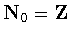 . .
Proposition 2.4
The normalizers of the subgroups
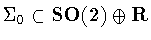
have the form
where the subgroup
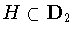
is as given in Table 1.
Proof: Since
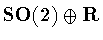 is abelian, it is clear that
is abelian, it is clear that
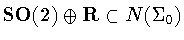 .
Hence .
Hence
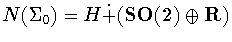 for some subgroup
for some subgroup
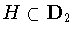 .
We compute that .
We compute that
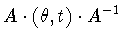 is the element
is the element
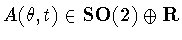 .
Hence, H consists of those elements .
Hence, H consists of those elements
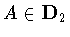 that preserve
that preserve 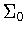 .
The element .
The element
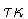 acts as -I on
acts as -I on
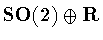 and so is always contained
in H. It follows that
and so is always contained
in H. It follows that
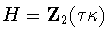 or
or
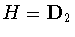 .
It now suffices
to determine whether or not .
It now suffices
to determine whether or not 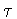 preserves
preserves 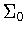 ,
that is, whether
or not ,
that is, whether
or not 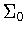 is preserved by the transformation
is preserved by the transformation
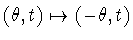 . .


Next: Untwisted Symmetry Groups
Up: Symmetries of Columns
Previous: Symmetries of Columns
Marty Golubitsky
2001-01-29
|