|
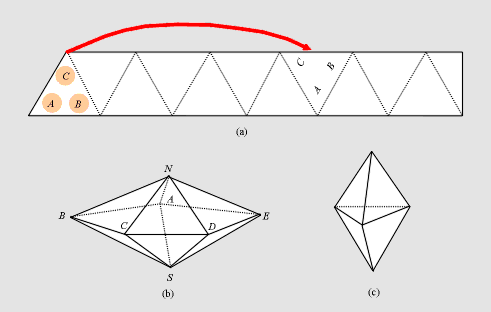
Figure 5: (a) Left-hand end of pattern piece;
(b) Pentagonal dipyramid; (c) Triangular dipyramid.
|
Figure 5(a) shows the left-hand end of the 31-triangle strip used to
construct the pentagonal dipyramid (with the colored side up). You should
mark the first and eighth triangles exactly as shown (note the orientation of
each of the letters within their respective triangles). To assemble the
model place the first triangle over the eighth triangle so that the circled
letters A, B, C are over the uncircled letters
A, B, C, respectively. Holding those
two triangles together in that position, you
will notice that you have the frame of a double pyramid for which there will
be five triangles above and five triangles below the horizontal plane of
symmetry (the plane containing the vertices 1, 2, 3, 4, 5 in
Figure 5(b)). Now hold this configuration up and turn it so that the long
strip of triangles falls around this frame. If the creases are folded well,
the remaining triangles will fall into place. When you get to the last
triangle there will be a crossing of a strip that the last triangle can tuck
into, and your model will be complete and stable.
If you have trouble because the strip doesn't fall into place there are two
frequent explanations. The first (and most likely) reason is that you have
not folded the crease lines firmly enough. In that case all you need to do
is crease them again with more gusto! The second possible reason is that
the strip seems too short to reach around the model and tuck in. This may
be remedied by trimming a tiny amount from each edge of the strip.
An analogous construction may be made for the triangular dipyramid shown in
Figure 5(c). This model can be made from a strip of 19 equilateral
triangles. Knowing what the finished model should look like and that you
should begin by forming the top three faces with one end of the strip should
be sufficient hints.
You may discover that you can construct each of these dipyramids with fewer
triangles, but we chose the construction that produces the most balanced
model. You will note that both of these constructions place precisely three
thicknesses of paper on each face, except where the last triangle tucks in
(producing four thicknesses). In both cases, you could remedy this small
defect by cutting off half of the first and last triangle on the strip.
Now let us turn to the Platonic Puzzles.

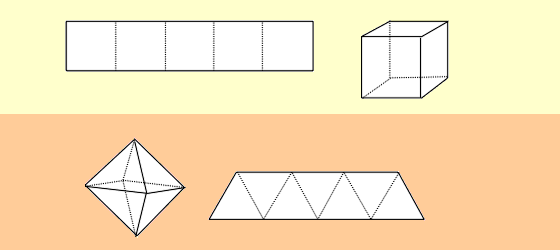
|
Figure 6: 1) Tetrahedron (2 strips); 2) Hexahedron (Cube) (3 strips);
3) Octahedron (4 strips); 4) Icosahedron (5 strips);
5) Dodecahedron (6 strips, 3 of each kind).
|
Figure 6 shows a typical puzzle piece (or strip) next to each solid, and
tells you how many are needed. In each case the puzzle is this: take the
required strips and braid them together to from the required solid in such a
manner that
(a) the same area is visible on each strip, and
(b) all ends are tucked in.
The tetrahedron, octahedron, and icosahedron all involve strips obtained
from the D1U1-folding procedure.
All you need to do is prepare the
pattern pieces as we described above and try to assemble the models. You
may note that, on all of these models, if you take into account the coloring
of the surface, they will have lost some of the symmetry you would expect to
find on Platonic Solids; that is, not all edges will look the same. For
some edges the two adjacent faces will have the same color but, for other
edges, the two adjacent faces will have different colors. (We will propose
another type of construction that corrects this defect in
Section 5). If
you manage to get all three of these together without any hints you are
really an expert! If you have trouble getting your models together check
the hints given in Section 4.
The hexahedron (cube) pattern pieces may be made by making exact folds on the
tape. All that you need to remember is that if you fold the tape directly
back on itself you will produce an angle of precisely p/2,
and if you bisect that angle you will know exactly where to fold the tape
back on itself to produce a square. Once you have one square on the tape
you may then simply fold the tape back and forth, accordion style, on top of
this square to produce the required number of squares. There are actually
two ways to braid these three pieces together to satisfy the conditions for
the puzzle. One of these ways produces a cube with opposite faces the same
color and the other way produces a cube with certain pairs of adjacent faces
the same color. From the point of view of symmetry the first is more
symmetric because, on that model, all edges abut two faces of different
colors. If you have trouble assembling this model check the hints given
in Section 4.
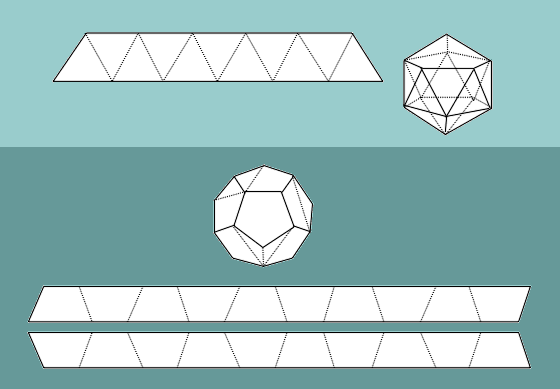
The dodecahedron involves strips obtained from the
D2U2-folding
procedure. But notice on the final pattern piece you should only fold the
pattern piece firmly along the short crease lines (ignoring the long lines)
after you have cut out each piece. We should tell you that on this model
four sections of each strip will overlap (for stability). It may also be
helpful to let you know that the strips go together in pairs and the
construction is then similar to that of the more symmetric cube you have
constructed above - and, if coloring is taken into account, the completed
model loses a lot of the symmetry you expect to see on a dodecahedron. You
may now have enough hints, but if you have difficulty consult
Section 4.
The diagonal cube involves four strips each containing 7 right isosceles
triangles as shown in Figure 7(a). The strips for these pieces may be
folded by the exact procedure similar to that described above for the cube in
the Platonic Puzzles. Just remember that this time you want to emphasize
those crease lines that make an angle of p/4 with the edges
of the tape. To assemble the cube you begin by laying out the four pieces
as shown in Figure 7(b), with the colored side of the paper not showing.
You may wish to put a small piece of tape in the exact center to hold the
strips in position. Now, thinking of the dotted square surrounding the
center as the base of your cube, you begin to braid the strips to make the
vertical faces, remembering that each strip should go successively over and
under the strips it meets as it goes around the model. When you get to the
top face you will find that all the ends will tuck in to produce a very
beautiful and highly symmetric cube; indeed, none of the symmetry of the cube
has been lost. You will notice that every face has a different arrangement
of four colors and that every vertex is surrounded by a different arrangement
of three colors.
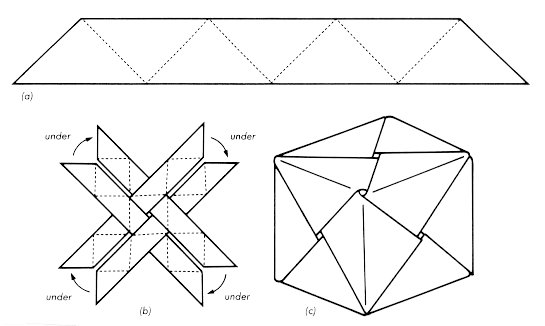
Figure 7
The golden dodecahedron involves strips obtained from the
D2U2-folding
procedure. But notice on the pattern pieces you should only fold the
pattern piece firmly along the long crease lines (ignoring the short lines)
after you have cut out each piece. To complete the construction of this
model, begin by taking five of the strips and arranging them, with the colors
showing, as shown in Figure 8(b),
securing them with paper clips at the
points marked with arrows. View the center of the configuration as the
North Pole. Lift this arrangement and slide the even-numbered ends
clockwise over the odd numbered ends to form the five edges coming south from
the arctic pentagon. Secure the strips with paper clips at the points
indicated by crosses. Now weave in the sixth (equatorial) strip, shown
shaded in Figure 8(c), and
continue braiding and clipping, where necessary,
until the ends of the first five strips are tucked in securely around the
South Pole. Above all, keep calm, you can even take a break - the model
will wait for you! Just make certain that every strip goes alternately over
and under each strip it meets all the way around the model. When the model
is complete (with the last ends tucked in) you may remove all the paper clips
and the model will remain stable. We notice that this constructed
dodecahedron is aesthetically very satisfying - more so than the
dodecahedron previously described. This is due to its amazing symmetry -
none of the possible symmetry has been lost.
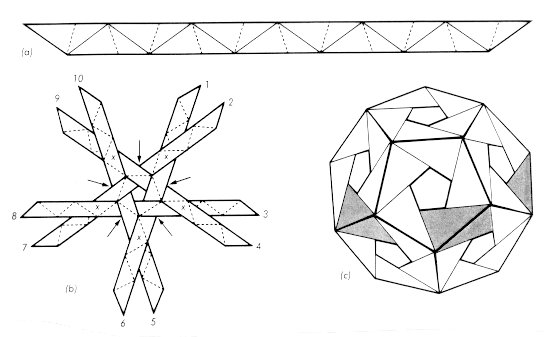
Figure 8
Before giving you the hints for the remaining models we cannot resist showing
you a lovely use for the cube with three strips, the diagonal cube and the
golden dodecahedron. An interesting question5
that has been asked by geometers (see [KW]) is "How many
disjoint pieces - both finite and infinite (or unbounded) - are formed
by the extended face planes6
for each Platonic solid?" As it turns out we can use our braided
models to answer some of these questions in the case of the unbounded
regions.
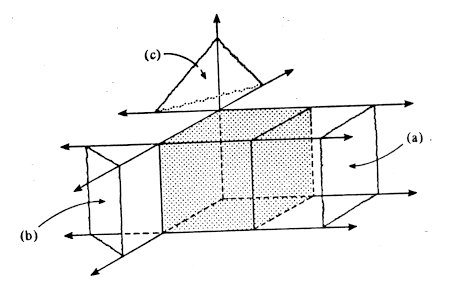
Let us use the ordinary cube to show how the braided models are useful.
Notice that the edges of the three strips used to create the braided model
lie in 6 planes which interesect each other to form a cube. Figure 9,
suitably interpreted, shows that the extended face planes of a cube partition
space into 27 pieces. There is, of course, the cube itself, which is
bounded. Then come the unbounded regions. There are
(a) 6 unbounded square prisms from its faces,
(b) 12 unbounded wedges from its edges and
(c) 8 unbounded trihedral regions from its vertices.
Now if you examine your braided cube you will see that there are
(a) 6 square regions that are covered with precisely two thicknesses of paper,
(b) 12 small slits along the edges where there is just one thickness of paper and
(c) 8 tiny triangular holes at the vertices.
This observation gives us the clue
as to how braided models may be useful more generally in answering our
question.
|
Figure 9: Using the braided cube to count the unbounded regions created
by the extended face planes of the cube.
|
What turns out to be true is that the braided models partition the surface of
the polyhedron into mutually disjoint sets of 'polygons' where each polygon
is covered by 0, 1 or 2 thicknesses of paper. The polygons where
there are holes (0-thickness) define unbounded polyhedral regions, the
polygons which are narrow slits (1-thickness) define unbounded wedges, and
the polygons where the strips actually are crossing each other (2
thicknesses) define unbounded prisms. The shapes of these unbounded regions
may vary with the braided model, but these general statements always hold.
If we are to be able to answer our question for the octahedron we need a
braided model with 4 strips so that their edges will define 8 face
planes - and, of course, the braided model should also have the same
symmetry group as the octahedron. Fortunately the diagonal cube satisfies
our conditions (see [Math] concerning the duality of the cube
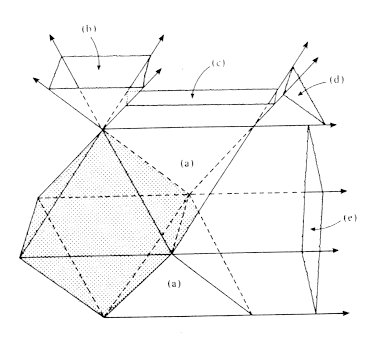
and octahedron). Figure 10 shows the octahedron with
some of its face
planes extended so that you can see a typical finite region and typical
unbounded regions of each type. The braided models don't help to count the
bounded regions (in this case, however, we can see from the part of
Figure 10
labeled (a) that there is a tetrahedron on each face of the original
octahedron). The rest of the labels in Figure 10
indicate unbounded regions
and Figure 11 reproduces
those regions as they are associated with the
surface of the diagonal cube. Thus, using Figure 11,
we may now count the
unbounded regions. They are (using the labels in Figure 11):
(b) 6 unbounded tetrahedral regions from the holes in the center of the faces,
(c) 24 unbounded wedges from the 4 slits on each of the 6 faces,
(d) 8 unbounded trihedral regions from the vertices,
(e) 12 unbounded, prism-like regions from the crossings of the
strips on the edges
comprising a total of 50 unbounded regions.
|
Figure 10: Extending the face planes of an octahedron.
|
So the golden dodecahedron must also be useful. In fact it is composed of
six strips and the planes defined by the edges of those strips intersect
inside this model to form a dodecahedron. Thus the surface of the golden
dodecahedron can be used to see that there are 122 unbounded regions created
by the extended face planes of the dodecahedron. You might like to try to
count them yourself using your golden dodecahedron (or see [P]
for more details).
What about the icosahedron? Figure 11 shows
how a model, braided from 10 straight strips, may be made from the
D2U2-tape that can be used to
count the 362 unbounded regions created by the extended face planes of
the icosahedron (see [P] for more details). We have not
written down anywhere how to make the model shown in Figure 11,
but we're sure the interested reader will be able to figure it out from what we have
said and the illustration.
You may be asking yourself why we have slighted the
tetrahedron. The answer is that the tetrahedron does not have faces lying
in opposite parallel planes, so our models are not useful here. However, it
is not difficult to imagine extending the face planes of the tetrahedron and
seeing that you have one finite region (the tetrahedron) and 14 unbounded
regions (4 from vertices, 6 from edges and 4 from faces).