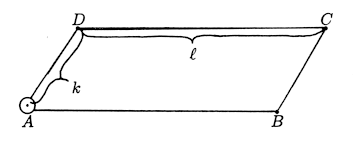
in the Pascal Triangle with sides in the coordinate directions n=constant,
r=constant (see Figure 1(b)), and vertices
| A = |
æ
ç
è |
n
r |
ö
÷
ø |
, B = |
æ
ç
è |
n
r+l |
ö
÷
ø |
, |
|
| C = |
æ
ç
è |
n-k
r+l |
ö
÷
ø |
, D = |
æ
ç
è |
n-k
r |
ö
÷
ø |
|
|
one calculates the weight
and discovers it is invariant under the action of sliding
the parallelogram in the direction n-r=constant. It is also
invariant under the involution I that exchanges the roles of k
and l. Notice that the vertex A, which we describe as the
anchor of the parallelogram, is fixed under I.
Let P*=AB*C*D*
be the image of P under I. Then, since
and W(P)=W(P*), we see that
Figure 2 should make it plain why we have described (0.1) as a Star
of David Theorem. It is very substantially generalized from the original
special case [1], in which no distortion of the star takes
place.
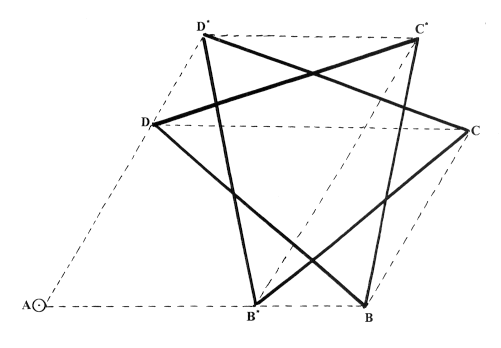
Figure 2.
The pattern becomes even clearer if we adopt the full binomial notation
with r+s=n, for the binomial coefficient.
For then it is natural to expect -
and easy to prove - that there are,
in fact, three such patterns, in which the sides of the fundamental
parallelogram are in two of the coordinate directions n=constant,
r=constant, s=constant, and sliding takes place in the third direction.
One need not even confine the action to the Pascal Triangle; these patterns
also hold in the Pascal Hexagon. Thus a fundamental parallelogram may be
slid across a 'zero' region (where, of course, the weight takes the form
0/0) into another non-zero region and recover the original weight
in the new region.
In this paper we are concerned with generalizing these ideas to the
multinomial coefficients
Let us first consider the case m=3 so that
trinomial coefficients are in question. Anticipating the more
general case, we will write
instead of the more usual
which features in Figures 5, 6,
and 7
next we consider a fundamental parallelepiped P,
with vertices
A C E G
B D F H
where
| A |
æ
ç
è |
|
|
|
ö
÷
ø |
, C |
æ
ç
è |
|
|
|
ö
÷
ø |
, |
|
| E |
æ
ç
è |
|
|
|
ö
÷
ø |
, G |
æ
ç
è |
|
|
|
ö
÷
ø |
, |
|
| B |
æ
ç
è |
|
|
|
ö
÷
ø |
, D |
æ
ç
è |
|
|
|
ö
÷
ø |
, |
|
| F |
æ
ç
è |
|
|
|
ö
÷
ø |
, H |
æ
ç
è |
|
|
|
ö
÷
ø |
(0.2) |
|
We describe the vertices A, C, E, G,
as the even vertices, and B, D, F, H
as the odd vertices, because the number of different
edges traversed between the anchor A and the vertex in question (regardless
of the length of the edge) is an even number for A, C, E, G,
and an odd number for B, D, F, H.
This fact may be seen by counting
the number of edges between the anchor and the vertex, on the illustration in
Figure 3.
Equivalently, the parity may be determined by counting the number
of ki's that are changed in the bottom of the symbol
This method will, of course, be useful when we generalize to higher dimensions.
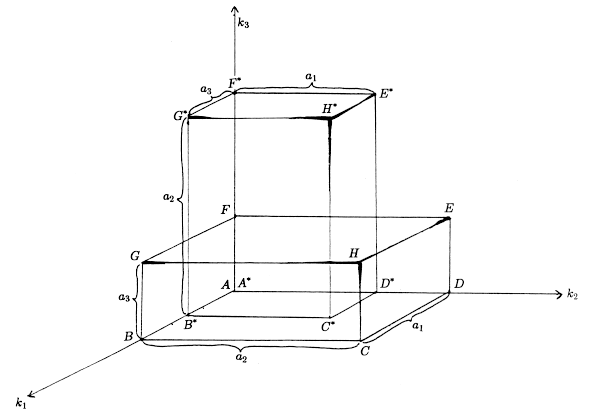
Figure 3.
The weight of P is given by
| W(P) = |
product of
even vertices
product of odd
vertices |
= |
A×C×E×G
B×D×F×H |
, |
|
so that, by a straightforward calculation,
| W(P) = |
n!(n+a1+a2)!(n+a2+a3)!(n+a1+a3)!
(n+a1)!(n+a2)!(n+a3)!(n+a1+a2+a3)! |
(0.3) |
|
Thus, for fixed a1, a2,
a3, W(P) is independent of
k1, k2, k3,
and invariant under the action of sliding P in the
plane n=constant. Further, the symmetric group S3 acts on
the triple (a1, a2,
a3). For any
p ÎS3
let P* be the p-image of P,
with its vertices labelled in the obvious way. Then A is invariant under
p and we get a Hyperstar of David Theorem
of the form
| B*×C×D*×E×F*×G×H*
= B×C*×D×E*×F×G*×H
(0.4) |
|
If p is a cyclic permutation of length
3 (as illustrated in Figure
3), then (0.4) is a genuinely new identity. However, if p
leaves some aj fixed, then (0.4) degenerates to a disguised
form of (0.1). Thus if p simply exchanges a1
and a2, then p leaves both the anchor A
and the vertex F fixed (F*=F), and (0.4)
is a simple consequence of the two Star of David identities
at 'levels' k3 and k3+a3,
respectively (see Figure 4).
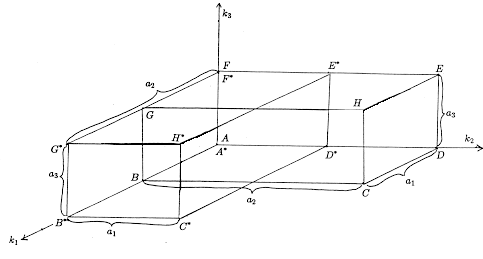
Figure 4.
Our other concern is to extend the domain of the multinomial coefficients
to permit any integer values of n, k1, k2,
..., km, subject, of
course, to the identity n=k1+k2+...
+km.
The case m=3 is then of special geometrical interest. In this
case it is natural to ask "What is the 3-dimensional analogue of the
Pascal Hexagon?" We certainly expect the analogue of the Pascal Triangle
to be the Pascal Tetrahedron (see Figure 5).
In fact, extending the Pascal
Tetrahedron in 3-dimensions, in a manner analogous to extending the
Pascal Triangle in 2-dimensions, produces a certain semi-regular
(Archimedean) polyhedron. Here we are content briefly to identify it as the
cuboctahedron, but in an Appendix to this paper we give the complete answer
to our question along with many features of the analogy.
A useful piece of information concerning this polyhedron is found in
Section 2; namely, for general m, if n is negative, then
will be non-zero if and only if exactly one of the ki
is negative. If, for example, k1<0, then, in fact,
|
æ
ç
è |
|
|
|
ö
÷
ø |
= (-1)n-k1 |
æ
ç
è |
|
|
|
ö
÷
ø |
(0.6) |
|
These (generalized) multinomial coefficients may then be used to provide
power series expansions of (a1+a2+...
+am)n, for n<0 in suitable
domains of Rm.
In Section 1 we describe the properties of weights of fundamental
hyperparallelepipeds (hppd's) in dimension m. We formulate and
establish a general Hyperstar of David Theorem. In
Section 2 we extend
the Pascal m-simplex of multinomial coefficients to allow
n to be a negative integer, and justify formula (0.6). In
Section 3 we discuss generalizations of our results. In particular we
point out that the multinomial coefficients may be replaced by suitable
separable functions of the variables n, k1,
k2,...,km. We are also concerned in this
section with generalizing an interesting observation of Hoggatt-Alexanderson
[6] relating to the 'nearest neighbours' of a given multinomial
coefficient
Finally, in the