|
Isometric transformations and symmetry groups The first steps in the development of the theory of symmetry in the 18th century stem from basic isometric transformations - mirror reflections (Fig. 1.2). Their combinations create all kinds of plane isometric transformations (transformations of congruence, or simply, isometries). Geometric transformation is an isometry (transformation of congruence) if it preserves the distance (metrics), i.e., if each pair of points X and Y are transformed into points X1 and Y1 in such a way that the distance between points X and Y is congruent to the distance between X1 and Y1 (Lopandic, 1979, Martin, 1982). This means that for every pair of the points X,Y and their images X1=t(X), Y1=t(Y) holds XY @ X1Y1. A typical example of isometric transformation (transformation of congruence) is the physical motion of a solid, where the distance between any two of its points remains unchanged (congruent) and consequently, the whole solid itself remains unchanged. However, the motion of fluids (for example, the vapor in clouds) does not have this characteristic.
Figure 1.2. A mirror reflection and examples of mirror-symmetric figures.
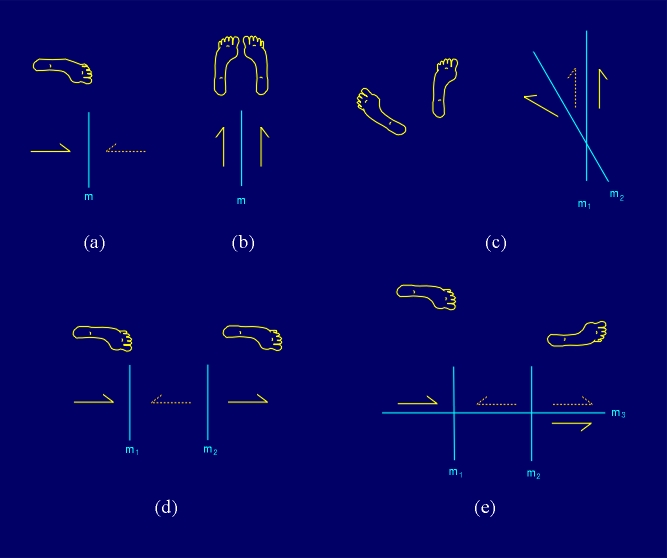
Of course, besides movements in a plane (space), i.e., direct transformations which preserve the orientation, indirect transformations are also isometries. They are the ones that change the orientation of the figure subject to them. All plane isometric transformations can be expressed as compositions of a maximum of three mirror reflections. This fact allows the complete classification of plane isometries (Fig. 1.3). Besides identical transformation, isometric transformations also include mirror reflection, rotation around the center, translation (parallel movement), and glide deflection ("footprints in the snow"). Identical transformation, rotation and translation are physical motions, i.e., direct transformations which do not change the orientation, while mirror and glide reflections make up a set of indirect transformations which do change the orientation of a figure (Lopandic, 1979; Martin, 1982).
Figure 1.3 a) Mirror reflection; b) rotation around the center; c) translation (parallel movement); d) glide reflection ("footprints in the snow").
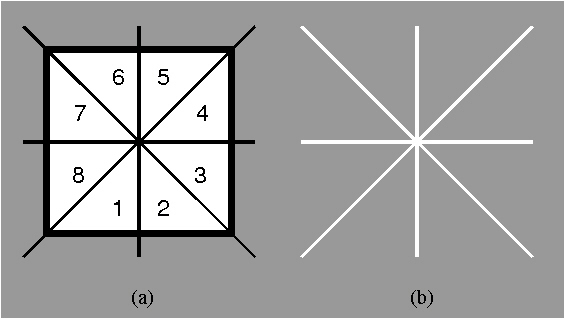
All transformations are compositions of mirror reflections. Direct (sense-preserving) isometries are compositions of an even number of reflections, and sense reversing of an odd number of reflections. After determining the five plane isometric transformations, we begin the study of plane symmetry structures, i.e., symmetric objects. The description of the symmetry of an object is based on determining all symmetries it comprises of, i.e., all transformations that leave it unchanged. All the symmetries of a figure make up a group of symmetries of that figure. The essential characteristic of the symmetries of any figure is the fact that a composition (subsequent performance) of any two of them also represents the symmetry of the same figure (Fig. 1.4).
As a result of the combinations of the five mentioned isometric transformations we get two infinite classes of groups of the symmetry of rosettes, seven groups of symmetry of friezes, and seventeen groups of symmetries of plane ornaments. In a similar manner, there are 230 groups of symmetry in 3D-space which completely define the symmetry of crystals. All these results are the fruits of mathematical crystallography in the 19th century (Shubnikov and Koptsik, 1972).
|