|
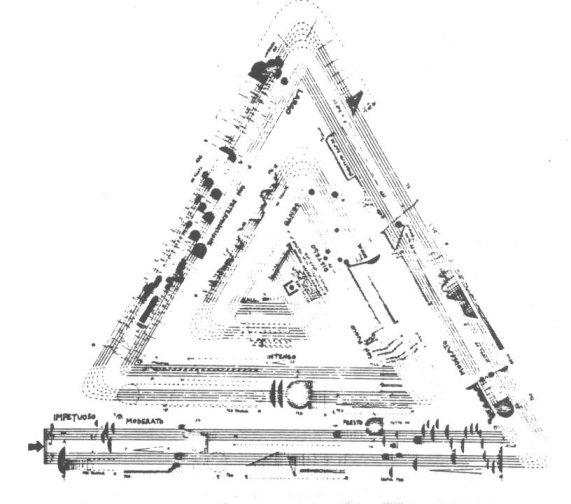
Visual modeling of musical works and their symmetry structure When conducting a symmetry analysis of different structures it is almost always necessary to recur to their visual modeling. In the case of music, its visual model - the notes, is inseparable from the musical piece itself and represents its concept. The line connecting a musical piece and its visual diagram interpretation, which allows the study of its symmetry structure, is sometimes almost direct (Fig. 1.9) (Donnini, 1986).
(a)
(b)
(c)
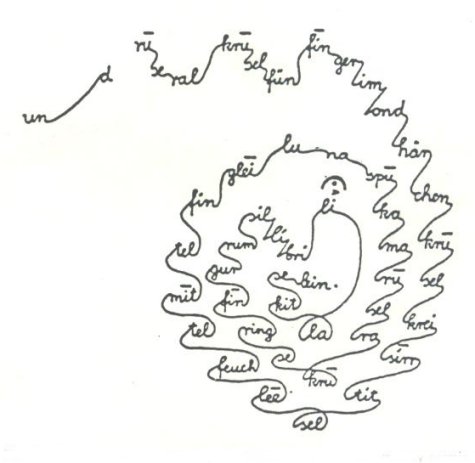
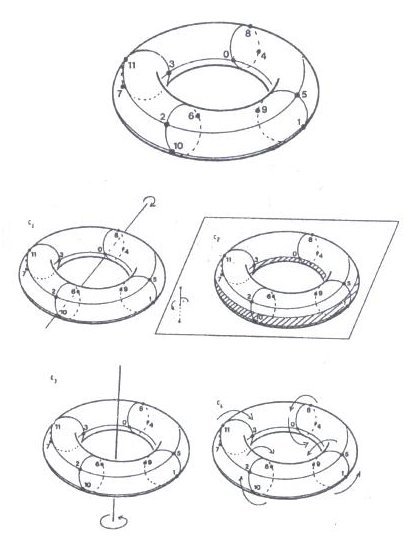
Different musical elements or the structure of a piece is frequently successfully modeled by elementary geometric symmetric figures such as a circle (Figs. 5.1-5.8), torus (e.g., the models of an interval-harmonic structures of tonality) (Fig. 1.10), or the spiral (Mazzola, Wieser, Bruner and Mazzulini, 1989). A good example of this type of structure with a spiral tonal organization (Fig. 1.11) is J.S. Bach's Wohltemperiertes Klavier, F. Chopin's 24 preludes, or P. Hindemith's Ludus Tonalis (Bruhn, 1992).
Figure 1.11 P. Hindermith's Ludus Tonalis, a spiral organization of the tone scheme. In the following chapters we have translated the terminology of the theory of symmetry to the language of music and have established the relationship between analogous rules. Because of the specific nature of the laws of symmetry in music, the theory of symmetry laws do not permit their direct (mechanical) transposition and application. This is why it is necessary to first define all specific properties, in the first place those dealing with local and global symmetry, and to create a special system of symmetry laws for the purpose of the symmetry analysis of musical works. An individual analysis of various components (rhythm, melody, harmony) of a musical piece has been conducted, as well as their superposition. The result of this is a complete symmetry analysis of a musical piece.
|