|
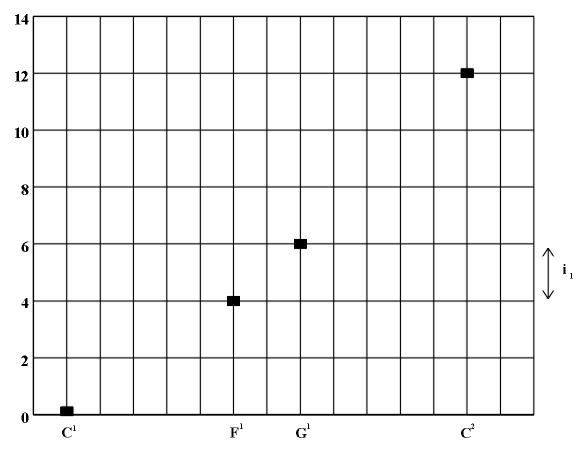
Scales with different semi-tone intervals The Pythagoreans derive their theory of musical harmony, which they identify with the harmony of a well-organized universe, based on the assumption that nature can be described by mathematical laws which boil down to proportion (arithmetic, geometric and harmonic) and are based on small integers (Ghyka 1987, p.38; Ghyka 1977, p. 4). Beginning with a sequence of small integers - tetrakis 1, 2, 3, 4 (Ghyka 1987, page 12), a sequence of their proportions (ratios) is formed - [1/2], [2/3], [3/4]. Based on the division of a string in these proportions, we get four basic tones: C1=1, C2=1/2, G1=2/3 and F1=3/4 and the unit interval (unit measure): F1-G1. Knowing that the frequency f(m) of a tone is the reciprocal value of the corresponding length of string m, f(m)=1/m, and that the interval i between two tones is the ratio of their frequencies, i=f(m):f(n)=n/m, then the proportion i1=2/3:3/4=8/9 gives the basic interval i1=F1-G1 (Fig. 3.2).
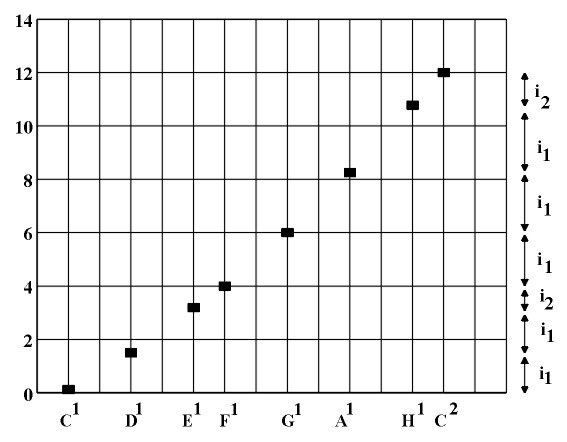
Figure 3.2 The frequencies of the basic tones of the Pythagorean scale and the unit interval F1-G1. In an attempt to measure all other intervals using the unit interval i1, with C1=1 and G1=1/2 as the starting points, the Pythagoreans determined that D1=8/9, and E1=8/92=[64/81], i.e., that A1=2/3◊8/9=[16/27], B1=2/3◊(8/9)2=[128/243]. However, due to the incommensurability of tetrachords C1-F1 and G1-C2 with a unit interval i1=8/9 chosen in this manner, the following intervals occur: i2=3/4:[64/81] = 1/2:[128/243] = [243/256] ~ 0.94922... Note that the interval i2 does not represent the exact value of the half tone - the length of the string which corresponds to the value of the half tone is obtained from the equation 2/3:x=x:3/4, i.e., x=[(Ö2)/2]. Consequently, the value of the half tone is [(i1)/2]=2/3:[(Ö2)/2]=[(2Ö2)/3] ~ 0.94281... Generally speaking, the length of string x which corresponds to the center of an interval is the geometric mean of the lengths of string m and n which correspond to the ends of the interval, i.e., x=Ö{mn}. The entire structure of such a distribution of intervals is multiplicative, i.e., it is defined by the products (ratios) of numbers which correspond to the lengths of the string. The result obtained is a sequence generated by fourths, fifths and octaves. If we take C1 as the initial tone and C2 as the end tone, we obtain the interval sequence i1 (C1-D1), i1 (D1-E1), i2 (E1-F1), i1 (F1-G1), i1 (G1-A1), i1 (G1-B1), i2 (B1-C2). Note that the this initial sequence is asymmetric, but that it allows tetrachords (C1-F1), (G1-C2) which satisfy translational symmetry, i.e. transposition. If we continue the tonic sequence in both directions, higher and lower, we obtain a periodic translational structure with the following period: 5i1+2i2=(C1-C2) which is a sequence of octaves of the tonal system. Since the initial interval sequence is assymetric, all of its points are non-equivalent and thus each one of them may serve as a starting point. The result obtained in this manner are seven modes (diatonic scales): Ionic, Doric, Phrygian, Lydian, Myxolydian, Aeolian and Locrian (Despic, 1987, Holopov, 1974). The principle of construction of a Pythagorean system based on perfect fifths results in the occurrence of deviation - the Pythagorean comma. This is the incongruence between a sequence consisting of twelve fifths and a sequence of seven octaves, i.e., the difference between the chromatic and diatonic half-tone (Despic, 1987).
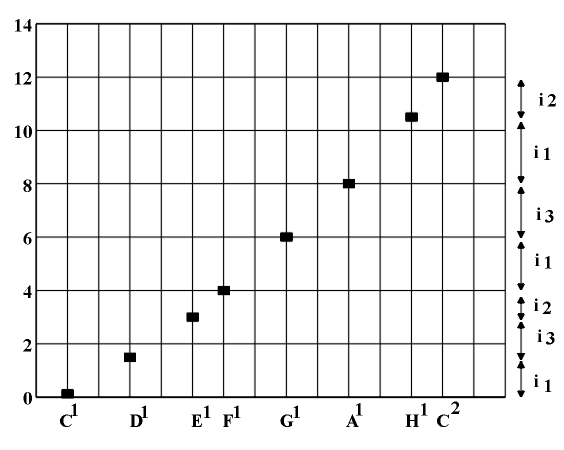
Figure 3.3 The frequency of tones and the interval structure of the Pythagorean scale. From the sequence [1/2], [2/3], [3/4], [4/5] results a natural or harmonic division of a string: C1=1, C2=1/2, G1=2/3, F1=3/4, E1=4/5. This sequence defines two intervals i1=8/9 (F1-G1), i2=[15/16] (E1-F1). Based on this we obtain the interval sequence i1 (C1-D1), i3 (D1-E1), i2 (E1-F1), i1 (F1-G1), i3 (G1-A1), i1 (A1-B1), i2 (B1-C2), where i3=[9/10] (Fig. 3.4).
Figure 3.4 The basic tones of a harmonic scale (C1, E1, F1, G1, C2), basic intervals (E1-F1), (F1-G1) and the interval structure of a harmonic scale. Of course, the occurrence of three different half-tone intervals caused deviations, particularly noticeable with keyboard instruments, as well as a significant increment of the complexity of the theory of intervals. The introduction of sharp and flat systems within the mentioned initial interval sequences, due to the difference between the half-tones, requires the discernment of chromatic and diatonic intervals and the corresponding scales. Thanks to the irregular division of an octave into 12 subintervals (an irregular half-tone sequence), the definition of the interval value is based on the name of the interval, as a function of the place of the particular tone in the scale, instead of as a real value of the interval, i.e., the difference in tonal pitch. The asymmetry of the initial system causes a high level of complexity of the entire structure which is especially visible, for example, in interval classification, their inversion rules and scale classification. This brings about the creation of instruments with keyboards (Žnharmonic instruments") where we note a difference between enharmonic tones (Encyclopedia of Music, 1963, p. 706).
|