|
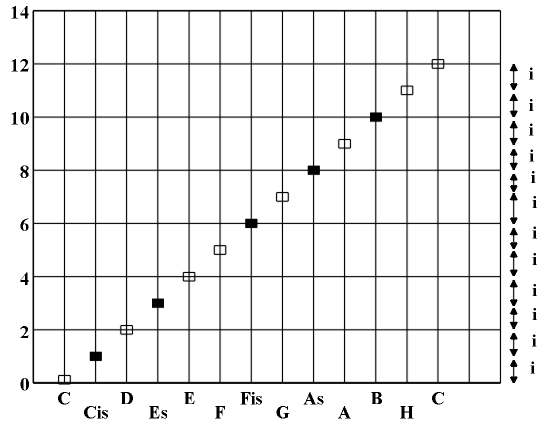
Tempering as the symmetrization of scales A solution to these problems is the introduction of tempered systems - an even distribution of 12 identical subintervals, half-tones, within the octave (Fig. 3.5). Since the octave is an interval with a value of 2, the value of each subinterval is 2[1/12]. The corresponding string lengths form a geometric progression : (1/2)0=1, (1/2)[1/12], (1/2)[2/12],..., (1/2)[12/12]=1/2. The ratio of its consecutive terms is the constant value of the halftones 2[1/12]. In this manner a complete symmetrization of the system has taken place and deviations have been eliminated, as well as the non-equivalence between sharps and flats and the difference between chromatic and diatonic half-tones. Because exponents add up (or are subtracted) when multiplying or dividing two degrees of the same number (aman=am+n), the complex multiplicative interval structure of the Pythagorean or harmonic system has been substituted by a simple additive structure made up of exponents. For example, the sum of intervals 2[7/12] and 2[5/12] is the product of their values 2[7/12]×2[5/12]=2([7/12]+[5/12])=2[12/12]=2 (octave), and the difference is the ratio of their values 2[7/12]:2[5/12]=2([7/12]-[5/12])=2[2/12]. Note that by tempering we achieve an approximation of the string lengths and, consequently, the corresponding pitch, where none of the intervals (except for the octave) coincide with the "perfect" harmonic intervals [2/3], [3/4], [4/5] (i.e., 2[7/12] » 2/3, 2[5/12] » 3/4, 2[4/12] » 4/5). Figure 3.5 The tempered system and its interval structure. |