|
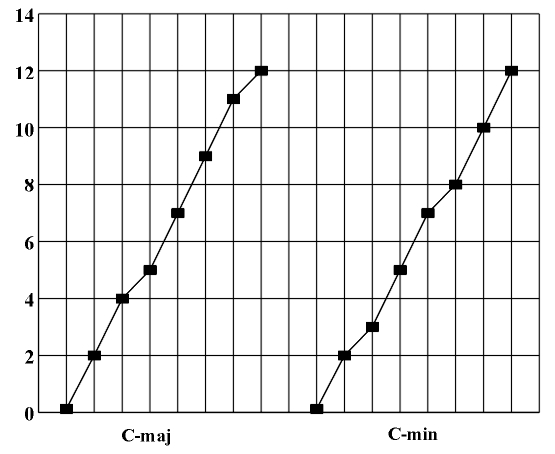
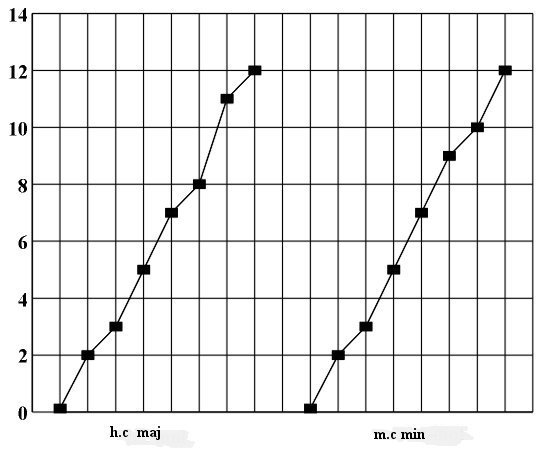
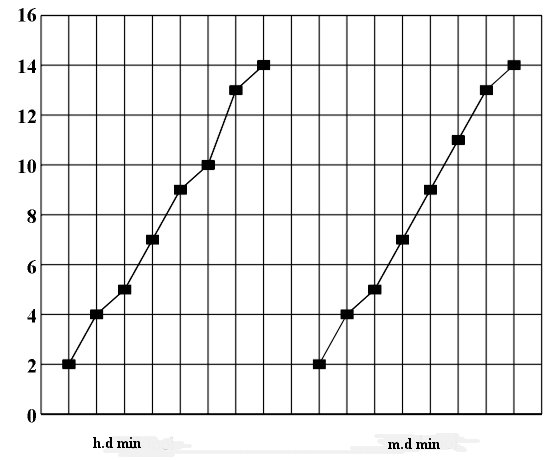
Formalized system for numerical notation of tonal pitches By switching to the tempered system, a complete symmetrization and a maximum simplification of the system has been achieved, something neither musical notation nor theory has completely put to use. For the purpose of this thesis we will create a formalized system which will help us conduct an exact study of the melodic structure of a musical piece and define symmetry regularities of its construction. Every structure is defined by its elements and their relationships. In the case of melodic structure this means that besides individual tones we must study their relationships, i.e., the intervals between the consecutive tones of a melody. Each interval is exactly defined by its starting point, its value and orientation (ascending or descending). By switching to a tempered system it is now possible to define the interval based on its value - the difference between the pitch of the end tone y2 and the initial tone y1 (i=y2-y1), not based on its place, or the name of the interval. Thus it is possible to differentiate between several equivalence classes of intervals: intervals of the same value, intervals of the same value and orientation, etc. Our unit measure for this is the half tone i1=2[1/12]. Because of the possibility of studying in the tempered system the additive system consisting of exponents instead of the multiplicative system, it is natural that we identify the value of each interval with the numerator of its exponent by using it as a lower index of interval. Thus, the value of the half-tone interval i1=2[1/12] which represents its unit measure can simply be denoted as 1, while the value of the interval i5=2[5/12] can be denoted as 5, etc. Afterwards, we simply work with the sums or differences of the positive integers obtained in this manner. Depending on its orientation (ascending or descending) each interval can be marked as + or -. In addition, each interval is defined by its starting point. Of course, this starting point must be defined in relationship to some universal referential system. Every referential system is defined by the initial point (or point 0) and by the unit measure. In our case the unit measure is the half tone 1, and it is natural to take tone C1 for our initial point y0=0. The classical five-line staff fully illustrates the tone and interval structure of C major, i.e., the distribution of the keys on the keyboard (Fig. 3.5), which makes it inadequate for a symmetry analysis of a musical piece. That is why in this thesis we will use the proposed coordinate system with a half-tone gradation on the y-axis. Because of periodicity, all scales will be given with y0 as their starting point and a sequence of intervals in (n=0,1,2,...,7), i.e., with a sequence of tonal pitches y0+in. All major scales will be given with a variable starting point and a sequence of intervals 0,2,4,5,7,9,11,12, where for C1 major (or simply C major) y0=0 (Fig. 3.6), for C-sharp major y0=1, for D major y0=2, for E-flat major (or D-sharp major) y0=3, for E major y0=4, for F major y0=5, for F-sharp major y0=6, for G major y0=7, for A-flat major (or G-sharp major) y0=8, for A major y0=9, for A-sharp major (or B minor) y0=10, for B major y0=11, etc. This means that C major can be expressed with the following sequence of tonal pitches 0,2,4,5,7,9,11,12, C-sharp major with sequence 1,3,5,6,8,10,12,13, D major with sequence 2,4,6,7,9,11,13,14, E-flat major with sequence 3,5,7,8,10,12,14,15, E major with the sequence 4,6,8,9,11,13,15,16, F major with sequence 5,7,9,10,12,14,16,17, F-sharp major with 6,8,10,11,13,15,17,18, G major with sequence 7,9,11,12,14,16,18,19, G-sharp major with sequence 7,9,11,12,14,16,18,19, A major with sequence 9,11,13,14,16,18,20,21, A-sharp major with sequence 10,12,14,15,18,20,22,23, B major with sequence 11,13,15,16,18,20,22,23, etc. Two scales are said to be equivalent if the difference between their initial tones is divisible by 12 (i.e., if for their initial tones y0 and y0¢ holds y0-y0¢=0 mod 12. This means that there are twelve non-equivalent major scales. We can derive 12 non-equivalent natural, harmonic and melodic minor scales in the same manner (Figs. 3.7 and 3.8). Every minor scale will also be exactly defined with its starting point y0 and an interval sequence in (n=0,1,...,7), i.e. with a sequence of tonal pitches y0+in. The corresponding sequence for a natural minor scale is 0,2,3,5,7,8,10,12, for the harmonic minor it is 0,2,3,5,7,8,11,12, and for the melodic minor scale is 0,2,3,5,7,9,11,12 (Figs. 3.7 and 3.8) Figure 3.6 C major scale and the natural C minor scale.
Figure 3.7 The harmonic and melodic C minor scale.
Figure 3.8 The harmonic D minor scale and the melodic D minor scale. We note that the translational symmetry of a tetrachord (transposition) occurs only in the major scales. For this reason we may say that every major scale is exactly defined by its lower tetrachord, i.e., the starting point y0 and the tetrachord interval sequence 0,2,4,5. Earlier on we mentioned that musical notation has not completely adhered to the simplifications brought about by introducing the tempered system, which resulted in the equivalence between sharps and flats. By applying a sharp, a tone whose pitch is y0 becomes y0+1, and by applying a flat, it becomes y0-1. In this manner in the tempered system the multiple use of sharps and flats in relationship to one tone becomes redundant. In the Pythagorean or harmonic system, the sequence of fifths or fourths is an infinite non-periodic sequence (Despic, 1987), wherefore it was necessary to pay attention to the initial point and number of steps. In a tempered system twelve fifths are identical to seven octaves and a sequence of fifths or fourths may be shown as a regular star-shaped heptagon {7/3} (Coxeter, 1961, p. 37), i.e., as a periodic sequence (Fig. 3.9). Figure 3.9 A sequence of fifths in a non-tempered (a) and a tempered (b) system. In order to derive all major scales using C major tones as starting elements, it is necessary to locate the elements of the tonal pitch sequence not found in the expanded sequence 0,2,4,5,7,9,11,12,14,16,17,19,21,23,24, which corresponds to C major. For example, in the case of D major which is defined with the sequence of tonal pitches 2,4,6,7,9,11,13,14 these elements are 6 and 13 and can be written down as 5+1 and 12+1 or -sharp 5, -sharp 12; thus, we naturally get a D major with two sharps. In the case of F major, defined with a sequence of tonal pitches 5,7,9,10,12,14,16,17, the number 10 which does not occur in the expanded sequence that corresponds to C major can be written as 9+1 or 11-1, or 9-sharp and 11-flat . In this case we employ another way of writing (11-flat ) because of our intention that the alternation mark should refer to all tones marked with 9. We cannot allow tones 9 and 9-sharp to appear simultaneously in the scale. The same method of reasoning may be applied to all scales. This means that the number of sharps or flats needed for denoting tones within a given scale depends on the number of elements in a sequence of tonal pitches of the scale studied, which are found in the expanded sequence of tonal pitches which corresponds to the initial scale (C major). A major scale with the initial tone Y0 and a natural minor scale with the initial tone y0 are called parallel scales if the difference between their tone pitches y0-Y0 when divided by 12 gives a remainder of 9 (y0-Y0=9 mod 12). As a result we get 48 scales: 12 major, 12 minor, 12 harmonic minor and 12 melodic minor, among which only three of them (harmonic D minor, harmonic G minor and melodic G minor) require the simultaneous use of sharps and flats. Thanks to the equivalence of sharps and flats, the following identifications occur: C-sharp = D-flat , D -sharp = E-flat , E=F-flat , E-sharp = F, F-sharp = G-flat , G-sharp = A-flat , A-sharp = B-flat , B=C-flat , B-sharp = C.
|