|
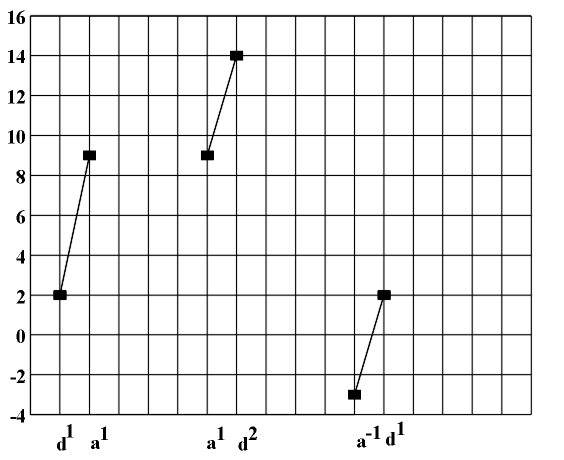
Intervals and chords in the formalized system In the course of our study of intervals we will examine three elements: the starting point, the value, and the orientation of the interval. Each interval is defined by the starting tonal pitch y1 and the difference in tonal pitches between the end tone y2 and the initial tone y1: i=y2-y1. For ascending intervals i is positive and for descending intervals i is negative. The inversion of a simple interval i is its complementary interval 12-i, (needed to complete the octave). This means that the inversion of an interval defined by tonal pitches y1, y2 is (y2,y1+12), or (y2-12,y1) (Fig. 3.10).
Figure 3.10 Inversion of interval (2,9) (D1-A1). In accordance to this kind of approach to intervals, we can define intervals 0, 7 and their inversions 12, 5 (completions to 12) as perfect consonants. These intervals correspond to the "perfect" first, fifth, octave, and fourth, respectively. Likewise, imperfect consonants are intervals 3, 4 and their inversions 9, 8, which correspond to the minor and major third respectively, or the minor and major sixth. The remaining simple intervals will be considered as dissonant. Intervals i and i1 may be considered equivalent if their difference is divisible by 12 (i-i1=0 mod 12). Complex intervals whose value exceeds 12 can be identified with simple intervals with which they are equivalent, i.e. we can apply vertical reduction of the interval. Each chord can be defined by the sequence of intervals forming it. Cord can be represented by the intervals:
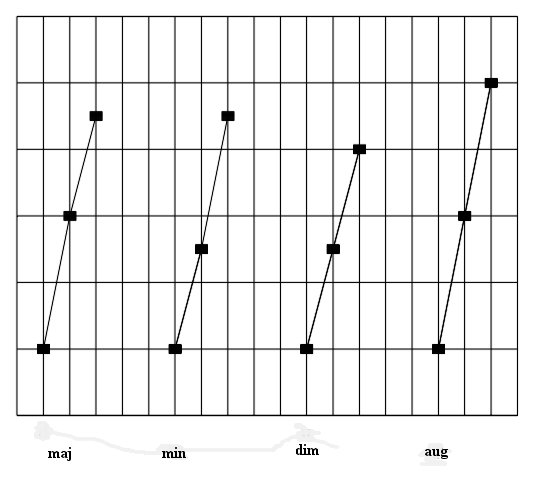
Consequently, there are, for example, four types of fifth-chord: major fifth-chord (0,4,7) or (4,3), denoted shortly by "maj", minor fifth-chord (0,3,7) or (3,4) ("min"), diminished fifth-chord (0,3,6) or (3,3) ("dim"), and augmented fifth-chord (0,4,8) or (4,4) ("aug") (Fig. 3.11) 1.
Figure 3.11 Major (maj), minor (min), diminished (dim) and augmented (aug) fifth-chord. We will find that the major and minor fifth-chords are asymmetric, whereas the diminished and augmented fifth-chords possess central symmetry. We can easily identify them as scale fifth-chords. For example, for a harmonic C minor scale there is a corresponding expanded sequence of tonal pitches (0,2,3,5,7,8,11,12,14,15,17,19,20,23,24). By constructing a fifth-chord with the starting point 0, we get a sequence of tonal pitches (0,3,7) which represents the minor fifth-chord (3,4). With 2 as the starting point, we get sequence (2,5,8) which represents a diminished fifth-chord (3,3). With 3 as the starting point we get a sequence of pitches (3,7,11) which represents an augmented fifth-chord (4,4). With 5 as the starting point we get sequence (5,8,12) which represents a minor fifth-chord (3,4). With 7 as the starting point we get sequence (7,11,14) which represents a major fifth-chord (4,3). With 8 as the starting point we get sequence (8,12,15) which represents a major fifth-chord (4,3). With 11 as the starting point we get a sequence (11,14,17) which represents a diminished fifth-chord (3,3). In this manner it is very easy to determine the versatility of each individual fifth-chord, i.e., all the places where it occurs. The first inversion of the fifth-chord assigned by a sequence of tonal pitches y1, y2, y3 is the sixth-chord (y2,y3,y1+12) (6), whereas its second inversion is a six-four chord (y3,y1+12,y2+12) (64). By an analogous procedure it is possible to identify seven types of seventh-chords: major seventh chord (0,4,7,11) or (4,3,4), dominant seventh chord (0,4,7,10) or (4,3,3), major seventh chord with minor third (0,3,7,11) or (3,4,4), minor seventh chord (0,3,7,10) or (3,4,3), leading seventh chord (0,3,6,10) or (3,3,4), diminished (0,3,6,9) or (3,3,3), and augmented (0,4,8,11) or (4,4,3). Three inversions of seventh-chord (y1,y2,y3,y4) are: six-five chord (y2,y3,y4,y1+12) (65), four-three chord (y3,y4,y1+12,y2+12) (43), and four-two chord (y4,y1+12,y2+12,y3+12) (2). In an analogous manner we can get twelve types of ninth chords and their inversions, etc.
|