Introduction

Related tonalities and symmetry of coefficients of similarity

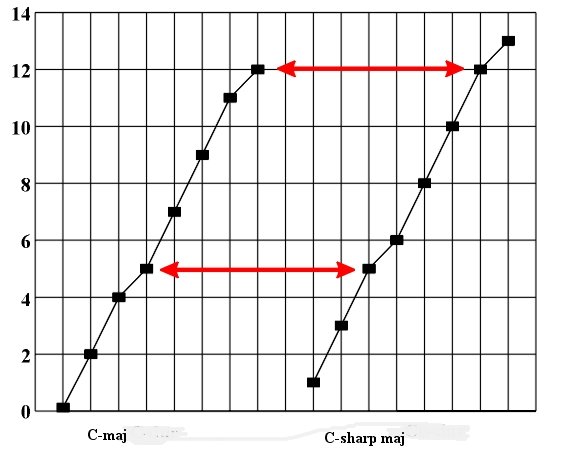
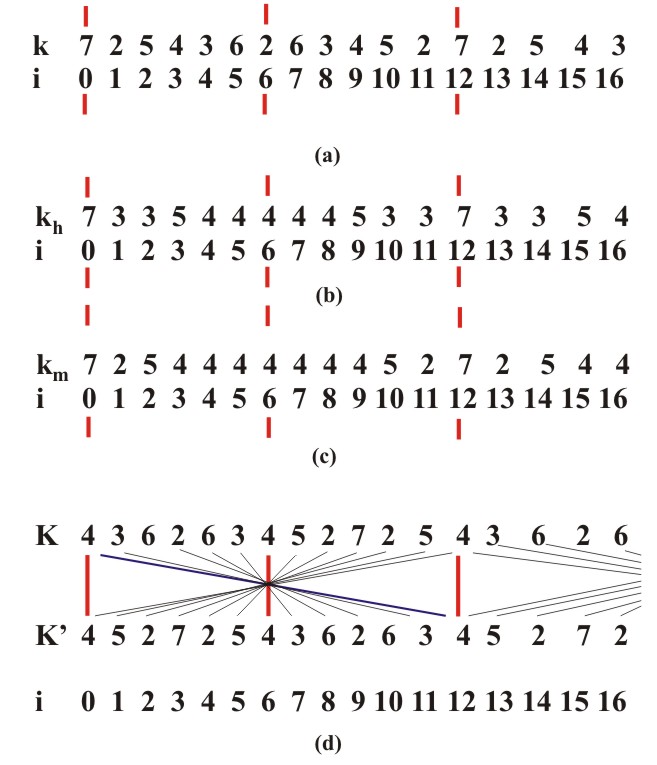
Within each scale we can differentiate between notes and foreign notes. For example for the C major scale, which is given as the sequence of tonal pitches 0,2,4,5,7,9,11,12, the foreign tones are 1,3,6,8,10. In the former part of our presentation it was already possible to note the significance of the basic symmetry transformation of tonal pitches - transposition, i.e., translation on the y-axis. Here every element y_n of the tone sequence is translated into y₀+y_n, i.e., it is translated on the y-axis for the value of the vector of translation y₀, thus forming together with the original tone the interval i=y₀. This is the procedure used for deriving all scales from basic interval sequences.

The next question refers to the degree of preservation of scale material of tones in regards to transposition. Since every major and natural minor scale is derived from the interval sequence 0,2,4,5,7,9,11,12, every harmonic minor scale from interval sequence 0,2,3,5,7,8,11,12, and every melodic minor scale from interval sequence 0,2,3,5,7,9,11,12, it is sufficient to study the preservation of the mentioned three interval sequences in regards to transposition. In this case, because of the periodicity of the mentioned sequences (with a period of 8), it is sufficient to study the effect of transposition on the first seven elements of the interval sequence. Also, because of the equivalence of every two scales with the same name (major, natural minor, harmonic minor, or melodic minor) whose difference of initial tone values is divisible by 12 (e.g., C minor and C² minor), it is sufficient to study only the results of transposition for the values i=y₀ (y₀=0,1,...,11).

Let us suppose that an interval sequence of 0,2,4,5,7,9,11,12 is given, as well as the expanded interval sequence 0,2,4,5,7,9,11,12,14,16,17,19,21,23,24 from which all major and natural minor scales are derived. If i=0, corresponding sequences have seven common tones, so the coefficient of preservation of the tone sequence is k(i)=k(0)=7. This coefficient is called the coefficient of similarity. If i=1, by transposing the first seven elements of the initial interval sequence 0,2,4,5,7,9,11,12, we get the transposed interval sequence 1,3,5,6,8,10,12. The elements 5,12 of this sequence belong to the expanded interval sequence 0,2,4,5,7,9,11,12,14,16,17,19,21,23,24. Since after the transposition for the interval i=1 only two elements of the transposed interval sequence belong to the expanded interval sequence, k(i)=k(1)=2 (Fig. 3.12) For i=2, by transposing the first seven elements we get the transposed interval sequence of 2,4,6,7,9,11,13, whose five elements 2,4,7,9,11 belong to the expanded interval sequence, and thus k(i)=k(2)=5.

Figure 3.12 Determining the coefficient of similarity for C major and C-sharp major (k=2).

By continuing to apply the same procedure we get a complete list of coefficients k(i) (i=0,1,...,11): k(0)=7, k(1)=2, k(2)=5, k(3)=4, k(4)=3, k(5)=6, k(8)=3, k(9)=4, k(10)=5, k(11)=2. The obtained sequence of coefficients k(i) is symmetric in regards to the number of inversions of its intervals (complementarity of intervals i and 12-i), i.e., it holds the following relation: k(i)=k(12-i). Hence, k(0)=k(12)=7, k(1)=k(11)=2, k(2)=k(10)=5, k(3)=k(9)=4, k(4)=k(8)=3, k(5)=k(7)=6, k(6)=2. Since all major and natural minor scales are derived from the same interval sequence 0,2,4,5,7,9,11,12, the obtained sequence of coefficients gives us two relevant pieces of information:

the number of scale tones which are translated into scale tones;
the interval structure of all major and natural minor scales.

The first piece of information points directly to related tonality. The degree of similarity between two major or two natural minor tonalities, whose difference of initial tonal pitches y₁ and y₂ is i=y₂-y₁, is equal to coefficient k(i)=k(y₂-y₁). For example, the degree of similarity of two equivalent (parallel) tonalities is k(0)=7; the degree of similarity between D major and A-flat major, whose initial tonal pitches are y₁=D=2 and y₂=A-flat = 8 is k(i)=k(y₂-y₁)=k(6)=2. The degree of similarity between natural A minor and natural F-sharp minor, whose initial tonal pitches are y₁=f-sharp = 6 and y₂=a=9 is k(i)=k((y₂-y₁)=k(3)=4, etc. The second piece of information comes from the fact that the value of the coefficient k(i) points to the level of occurrence of certain intervals within the mentioned scales, i.e., to the significance of each individual scale interval. Thus, a decreasing sequence of the coefficients k(i): k(0)=7, k(5)=k(7)=6, k(2)=k(10)=5, k(3)=k(9)=4, k(4)=k(8)=3, k(1)=k(6)=k(11)=2, directly proves the frequence of occurrence and significance of intervals 5,7 (fifth, fourth), 2,10 (second, seventh), 3,9 (third, sixth), etc., within these major and natural minor scales. In the case of complex intervals between the starting tonal pitches of two scales, i.e., intervals whose value exceeds 11, these are identified with simple intervals with which they are equal modulo 12.

Our next goals are:

to calculate the number of common scale tones that belong to a certain major and a certain natural minor scale, and
to determine the degree of similarity between tonalities that correspond to them.

The tone material of every natural minor scale represents the transposition of a parallel major scale for the interval i=9. Vice versa, the tone material of every major scale represents the transposition of a parallel natural minor scale for the complementary interval of i'=3. For this reason, the sequence of coefficients K(i), which offer relevant data on the relationship between a major scale with an initial tonal pitch of Y₀ and a natural minor scale with an initial tonal pitch of y₀, i.e., a major scale and a natural minor scale whose initial tones form interval i=y₀-Y₀, will be identical with the sequence of coefficients k(9-i) (K(i)=k(9-i)), i.e., with the former sequence of values k(i) nine places shifted. For the major and parallel natural minor scale K(9)=k(9-9)=k(0)=7. Then we get K(10)=k(9-10)=k(-1)=k(11)=2, K(11)=k(9-11)=k(-2) = k(10)=5, K(0)=k(9)=4, K(1)=k(8)=3, K(2)=k(7)=6, K(3)=k(6)=2, K(4)=k(5)=6, K(5)=k(4)=3, K(6)=k(3)=4, K(7)=k(2)=5, K(8)=k(1)=2.

We can obtain the same result if we start from the interval sequence 0,2,4,5,7,9,1,12 from which all major scales are derived and from the interval sequence 0,2,3,5,7,8,10,12 from which all natural minor scales are derived. By forming a decreasing sequence of coefficients K(i): K(9)=7, K(2)=K(4)=6, K(7)=K(11)=5, K(0)=K(6)=4, K(1)=K(5)=3, K(3)=K(8)=K(10)=3, and by starting from a fixed major tonality, we can form a corresponding sequence of natural minor tonalities according to their decreasing similarity.

By applying coefficients k(i) and K(i), we get a sequence of major and natural minor tonalities that starts with a major tonality of our choice and decreases similarity-wise. For example, in the case of C major:

	7	6	5	4	3	2
C major		F major	D major	E-flat major	E major	C-sharp major
		G major	B-flat major	A major	A-flat major	B major
						F-sharp major
	A minor	D minor	G minor	C minor	C-sharp minor	G-sharp minor
		E minor	B minor	F-sharp minor	F minor	B-flat minor
						D-sharp minor

At the same time this means that the number of common scale tones of any scale belonging to a column with a C major scale, will be equal to the coefficient at the top of the column. For example, D major, B-flat major, G minor, and B minor scales will each have five common scale notes with the C major scale.

By applying coefficients k(i) and K(i), or by a direct transposition of the previous table we can create an analogous table for every major tonality. For example, the analogous table for A flat major would be:

	7	6	5	4	3	2
A-flat major		C-sharp major	B-flat major	B major	C major	A major
		E-flat major	F-sharp major	F major	E major	G major
						D major
	F minor	B-flat minor	E-flat minor	G-sharp minor	A minor	E minor
		C minor	G minor	D minor	C-sharp minor	F-sharp minor
						B minor

All necessary conclusions can be drawn even without drawing complete tables. For example, if we wish to determine coefficient K(i), which links C-sharp major and natural F-sharp minor, it is sufficient to know that their initial tones are C-sharp , (Y₀=1) and F-sharp (Y₀=6), so that i=Y₀-y₀=5. Thus the coefficient is K(5)=3.

By taking advantage of the fact that from the given natural minor scale we cross over to its parallel major scale by a transposition the interval of i'=3, as a result we get a sequence of coefficients K'(i)=k(i-3) which is identical to sequence k(i) three steps shifted: K'(3)=k(0)=7, K'(4)=k(1)=2, K'(5)=k(2)=5, K'(6)=k(3)=4, K'(7)=k(4)=3, K'(8)=k(5)=6, K'(9)=k(6)=2, K'(10)=k(7)=6, K'(11)=k(4)=3, K'(0)=k(-3)=k(9)=4, K'(1)=k(-2)=k(10)=5, K'(2)=k(-1)=k(11)=2. By forming a decreasing sequence of coefficients K'(i): K'(3)=7, K'(8)=K'(10)=6, K'(1)=K'(5)=5, K'(0)=K'(6)=4, K'(7)=K'(11)=3, K'(2)=K'(4)=K'(9)=2, and by using coefficients k(i) and K'(i), we can build a sequence of natural minor and major tonalities which begin with a given minor and major tonality and decrease similarity-wise. For example, in the case of natural C minor (or simply, C minor) this sequence is:

	7	6	5	4	3	2
C minor		F minor	D minor	E-flat minor	E minor	C-sharp minor
		G minor	B-flat minor	A minor	G-sharp minor	B minor
						F-flat minor
	E-flat major	B-flat major	C-sharp major	C major	G major	D major
		A-flat major	F major	F-sharp major	B major	E major
						A major

By applying coefficients k(i) and K'(i), or directly, by transposing the previous table we can derive an appropriate table for every natural minor tonality we choose.

We can apply the same procedure on sequence 0,2,3,5,7,8,11,12 which defines all harmonic minor scales. In that case, we get a sequence of coefficients k_h(i): k_h(0)=7, k_h(1)=k_h(2)=k_h(10)=k_h(11)=3, k_h(3)=kh(9)=5, k_h(4)=k_h(5)=k_h(6)=k_h(7)=k_h(8)=4. Note that the specific interval structure of harmonic minor scales has brought about a difference in the significance of individual intervals, i.e., the special role of complementary intervals 3,9, the uniformity of the significance of intervals 4,5,6,7,8 and the inferiority of intervals 1,2,10,12. Since the mentioned groups of intervals correspond to coefficients k_h(i)=5,4,3 with which they are very close in value, it is evident that the difference in the significance of intervals is very small, i.e., all intervals are approximately of the same significance. In the case of harmonic minor scales we can also construct a table of similarity. For example, in the case of harmonic C minor (h. C minor) it looks like this:

	5	4	3
h. C minor	h. E-flat minor	h. E minor	h. C-sharp minor
	h. A minor	h. F minor	h. D minor
		h. F-sharp minor	h. B-flat minor
		h. G minor	h. B minor
		h. G-sharp minor

Analogous tables of similarity coefficients can be derived for all harmonic minor tonalities by applying coefficients k_h(i), or by direct transposition of the previous table. All harmonic minor scales that belong to the same column have common scale tones with the initial scale k_h(i). For example, harmonic E-flat minor and harmonic A minor share five common scale tones each with harmonic C minor.

In the case of interval sequence 0,2,3,5,7,9,11,12 which defines all melodic minor scales, the coefficients k_m(i) are: k_m(0)=7, k_m(1)=k_m(11)=2, k_m(2)=k_m(10)=5, k_m(3)=k_m(4)=k_m(5)=k_m(6)=k_m(7)=k_m(8)=k_m(9)=4. Note the domination of intervals 2,10, the uniformity of intervals 3,4,5,6,7, 8,9, and the inferior role of intervals 1,11. Based on the coefficients k_m(i) it is easy to derive tables of similarity of melodic minor tonalities. For example, for melodic C minor (m. C minor) we have:

	5	4	3
m. C minor	m. D minor	m. E-flat minor	m. C-sharp minor
	m. B-flat minor	m. E minor	m. B minor
		m. F minor
		m. F-sharp minor
		m. G minor
		m. G-sharp minor
		m. A minor

If we look at the previously derived sequences of coefficients k(i), k_h(i), k_m(i), K(i), and K'(i), we will note their mirror symmetry (Fig. 3.13). All the mentioned sequences of coefficients have been obtained by transposing the interval sequence which corresponds to the major and natural minor, harmonic minor and melodic minor scales, as well as by determining the number of tones which are transformed into scale tones by transposition. This means that these coefficients demonstrate a degree of invariance of major and minor, harmonic minor, or melodic minor tone intervals in relation to transposition. The obtained sequence of coefficients k(i), k_h(i), k_m(i) is symmetric in regards to the inversion of intervals (complementary intervals i and 12-i), i.e., in regards to the axis of symmetry which contains the center of the sequence, point 6 (the F-sharp tone), or in regards to the axis of symmetry in the point which is obtained by the translation of point 6 for the interval 9, as in the case of sequence k(i), or for interval 3 in the case of sequence K'(i). The translation of the axis of symmetry of a sequence is the result of the fact that the parallel natural minor scale is derived from a given major scale by transposition by the interval 9, or that the parallel major scale is derived from its corresponding natural minor scale by a transposition by the interval 3. Also, sequences K(i) and K'(i) are centrally symmetric with regard to the center of symmetry located in the center of the sequence, point 6 (Fig. 3.13 d). All the stated symmetry properties are the result of the fact that in the mentioned cases the degree of invariance is determined when some tonal (interval) material is transposed into the same tonal (interval) material.

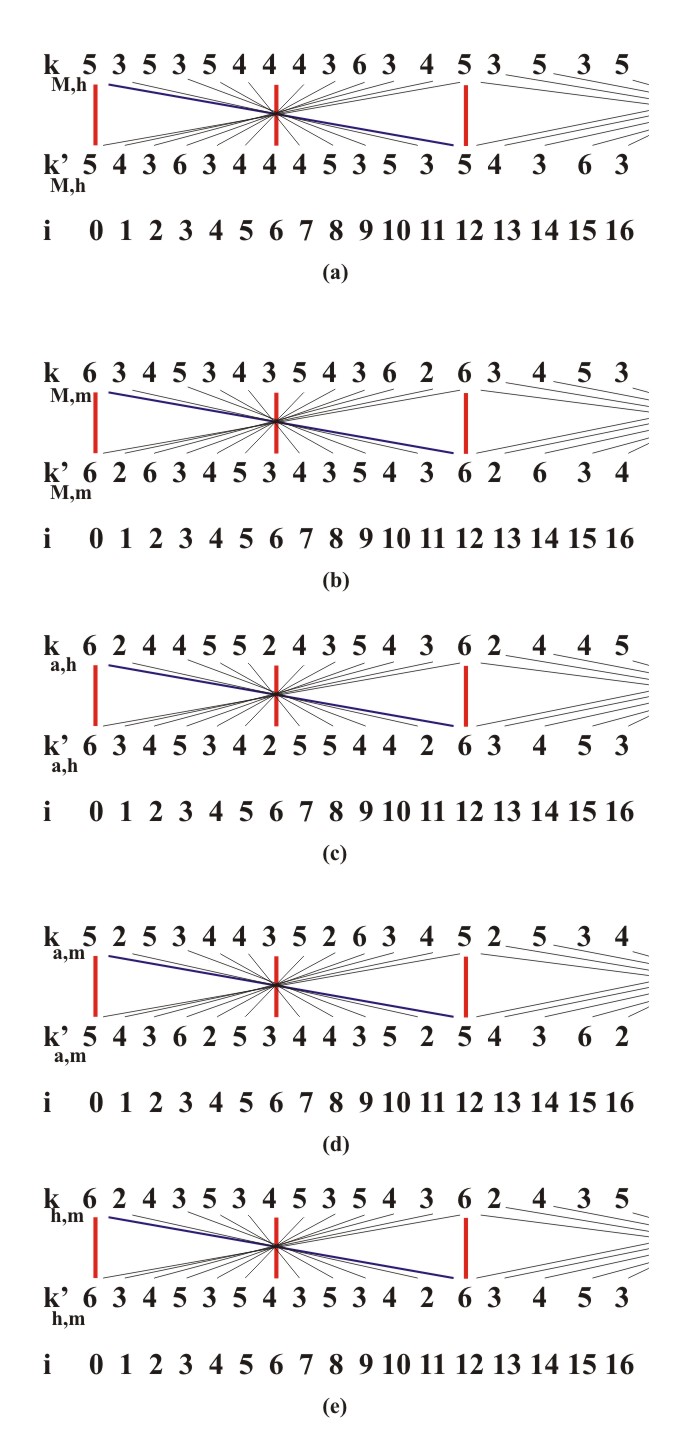
Figure 3.13 The mirror symmetry of similarity coefficients a) k(i); b) k_h(i); c) k_m(i), and the central symmetry of coefficients K(i) and K'(i) (d).

The next step represents the study of the same problem but in relationship to different initial and final material. Concretely, our goal is to determine coefficients of similarity of tonalities for the transposition from one tonal (interval) material to another, e.g., from major to harmonic minor, etc.) and vice versa, with the aim of constructing a table of tonality similarities for a transposition of this kind. The principle of assigning a coefficient of the similarity of tonalities is identical as in our previous case studies.

Beginning with interval sequence 0,2,4,5,7,9,11,12, from which all major scales are derived and interval sequence 0,2,3,5,7,8,11,12, from which all harmonic minor scales are derived, we get a sequence of coefficients of the similarity of tonalities k_M,h(i). They show the degree of similarity between a major tonality with the initial pitch of y₀ and a harmonic minor tonality with the initial pitch of y₀, where i=y₀-Y₀. The sequence of coefficients is: k_M,h(0)=5, k_M,h(1)=4, k_M,h(2)=3, k_M,h(3)=6, k_M,h(4)=3, kM,h(5)=4, k_M,h(6)=4, k_M,h(7)=4, k_M,h(8)=5, k_M,h(9)=3, k_M,h(10)=5, k_M,h(11)=3. This sequence is not a mirror symmetric and it has no maximum for i=0 (because k_M,h(0)=5), but for i=3 (because k_M,h(3)=6). The sequence of coefficients k_M,h'(i), which show a reverse connection between the given harmonic minor tonality and the major tonality, whose initial tones form interval i, is equal to sequence k_M,h(i) read backwards, i.e., k_M,h(i)=k_M,h'(-i)=k_M,h'(12-i), so k_M,h'(0)=5, k_M,h'(1)=3, k_M,h'(2)=5, k_M,h'(3)=3, k_M,h'(4)=5, k_M,h'(5)=4, k_M,h'(6)=4, k_M,h'(7)=4, k_M,h'(8)=3, k_M,h'(9)=6, k_M,h'(10)=3, k_M,h'(11)=4. Note the occurrence of central symmetry in point 6 which transforms the sequence k_M,h(i) into k_M,h'(i). It is the direct effect of the complementarity of intervals i and 12-i, i.e., the relation k_M,h(i)=k_M,h'(12-i).

In the same manner, beginning with interval sequence 0,2,4,5,7,9,11,12, from which all major scales are derived and interval sequence 0,2,3,5,7,9,11,12, from which all melodic minor scales are derived, we get a sequence of similarity coefficients for major and melodic minor tonalities k_M,m(i) and its inverse sequence k_M,m'(i): k_M,m(0)=k_M,m'(0)=6, k_M,m(1)=k_M,m'(11)=3, k_M,m(2)=k_M,m'(10)=4, k_M,m(3)=k_M,m'(9)=5, k_M,m(4)=k_M,m'(8)=3, k_M,m(5)=k_M,m'(7)=4, k_M,m(6) = k_M,m'(6)=3, k_M,m(7)=k_M,m'(5)=5, k_M,m(8)=k_M,m'(4)=4, k_M,m(9)=k_M,m'(3)=3, k_M,m(10)=k_M,m'(2)=6, k_M,m(11)=k_M,m'(1)=2. In this case the sequences k_M,m(i) and k_M,m'(i)=k_M,m(12-i) are centrally symmetric with regard to the center - point 6, but none of them is mirror symmetric.

By an analogous procedure, beginning with interval sequence 0,2,3,5,7,8,10,12 from which all natural minor scales are derived, interval sequence 0,2,3,5,7,8,11,12 from which all harmonic minor scales are derived, and interval sequence 0,2,3,5,7,9,11,12 from which all melodic minor scales are derived, we can calculate the sequence of coefficients of the similarity of tonalities k_a,h(i), k_a,h'(i)=k_a,h(12-i), k_a,m(i) = k_a,m'(i)=k_a,m(12-i), k_h,m(i), k_h,m'(i)=k_h,m(12-i). Those sequences are, respectively: k_a,h(0)=k_a,h'(0)=6, k_a,h(1)=k_a,h'(11)=2, k_a,h(2)=k_a,h'(10)=4, k_a,h(3)=k_a,h'(9)=4, k_a,h(4)=k_a,h'(8)=5, k_a,h(5)=k_a,h'(7)=5, k_a,h(6)=k_a,h'(6)=2, k_a,h(7)=k_a,h'(5)=4, k_a,h(8)=k_a,h'(4)=3, k_a,h(9)=k_a,h'(3)=5, k_a,h(10)=k_a,h'(2)=4, k_a,h(11)=k_a,h'(1)=3; k_a,m(0)=k_a,m'(0)=5, k_a,m(1)=k_a,m'(11)=2, k_a,m(2)=k_a,m'(10)=5, k_a,m(3)=k_a,m'(9) = 3, k_a,m(4)=k_a,m'(8)=4, k_a,m(5)=kp, m'(7)=4, k_a,m(6)=k_a,m'(6)=3, k_a,m(7)=k_a,m'(5)=5, k_a,m(8)=k_a,m'(4)=2, k_a,m(9)=k_a,m'(3)=6, k_a,m(10)=k_a,m'(2)=3, k_a,m(11)=k_a,m'(1)=4; k_h,m(0)=k_h,m'(0)=6, k_h,m(1)=k_h,m'(11)=2, k_h,m(2)=k_h,m'(10)=4, k_h,m(3)=k_h,m'(9)=3, k_h,m(4)=k_h,m'(8)=5, k_h,m(5)=k_h,m'(7)=3, k_h,m(6)=k_h,m'(6)=4, k_h,m(7)=k_h,m'(5)=5, k_h,m(8)=k_h,m'(4)=3, k_h,m(9)=k_h,m'(3) = 5, k_h,m(10)=k_h,m'(2)=4, k_h,m(11 )=k_h,m'(1)=3 (Fig. 3.14).

Figure 3.14 The central symmetry of the similarity coefficients a) k_M,h(i), k_M,h'(i); b) k_M,m(i), k_M,m'(i); c) k_a,h(i), k_a,h'(i); d) k_a,m(i), k_a,m'(i); e) k_h,m(i), k_h,m'(i).

Based on the previous calculations of coefficients k(i), k_h(i), k_m(i), K(i), K'(i) and coefficients k_a,h(i), k_a,h'(i), k_a,m(i), k_a,m'(i), k_h,m(i), k_h,m'(i), we can construct complete tables of the similarity of all tonalities for the given tonality, classified according to a decreasing sequence in regards to similarity. With this in mind, it is sufficient to construct four such tables: for C major, natural C minor (or simply C minor), harmonic C minor (h. C minor) and melodic C minor (m. C minor), whereas all other tables for any other given tonality may be derived by transposing these four tables.

	7	6	5	4	3	2
C major		F major	D major	E-flat major	E major	C-sharp major
		G major	B-flat major	A major	G-sharp major	B major
						F-sharp major
	A minor	D minor	G minor	C minor	C-sharp minor	G-sharp minor
		E minor	B minor	F-sharp minor	F minor	B-flat minor
						D-sharp minor
		h. E-flat minor	h. C minor	h. C-sharp minor	h. E-flat minor
			h. G-sharp minor	h. F minor	h. E minor
			h. B-flat minor	h. F-sharp minor	h. A minor
				h. G minor	h. B minor
		m. C minor	m. E-flat minor	m. D minor	m. C-sharp minor	m. B minor
		m. B-flat minor	m. G minor	m. F minor	m. E minor
				m. G-sharp minor	m. F-sharp minor
					m. A minor

	7	6	5	4	3	2
C minor		F minor	D minor	E-flat minor	E minor	C-sharp minor
		G minor	B-flat minor	A minor	G-sharp minor	B minor
						F-sharp minor
	E-flat major	B-flat major	C-sharp major	C major	G major	D major
		A-flat major	F major	F-sharp major	B major	E major
						A minor
		h. C minor	h. E minor	h. D minor	h. G-sharp minor	h. C-sharp minor
			h. F minor	h. E-flat minor	h. B minor	h. F-sharp minor
			h. A minor	h. G minor
				h. B-flat minor
		m. A minor	m. C minor	m. E minor	m. E-flat minor	m. C-sharp minor
			m. D minor	m. F minor	m. F-sharp minor	m. G-sharp minor
			m. G minor	m. B minor	m. B-flat minor

	6	5	4	3	2
h. C minor		h. E-flat minor	h. E minor	h. C-sharp minor
		h. A minor	h. F minor	h. D minor
			h. F-sharp minor	h. B-flat minor
			h. G minor	h. B minor
			h. G-sharp minor
	A major	C major	F major	C-sharp major
		D major	F-sharp major	E-flat major
		E major	G major	A-flat major
			B major	B-flat major
	C minor	E-flat minor	D minor	C-sharp minor	F-sharp minor
		G minor	F minor	E minor	B minor
		G-sharp minor	A minor
			B-flat minor
	m. C minor	m. E minor	m. D minor	m. E-flat minor	m. C-sharp minor
		m. G minor	m. F-sharp minor	m. F minor
		m. A minor	m. B-flat minor	m. G-sharp minor
				m. B minor

	6	5	4	3	2
m. C minor		h. m. D minor	m. E-flat minor		m. C-sharp minor
		m. B-flat minor	m. E-flat minor		m. B minor
			m. F minor
			m. F-sharp minor
			m. G minor
			m. G-sharp minor
			m. A minor
	C major	F major	E major	E-flat major	C-sharp major
	D major	A major	G major	F-sharp major
			B-flat major	A-flat major
				B major
	E-flat minor	C minor	C-sharp minor	D minor	E minor
		F minor	G minor	F-sharp minor	B minor
		B-flat minor	G-sharp minor	A minor
	h. C minor	h. E-flat minor	h. D minor	h. C-sharp minor	h. B minor
		h. F minor	h. F-sharp minor	h. E minor
		h. G-sharp minor	h. B-flat minor	h. G minor
				h. A minor