|
Optimization of melodic line
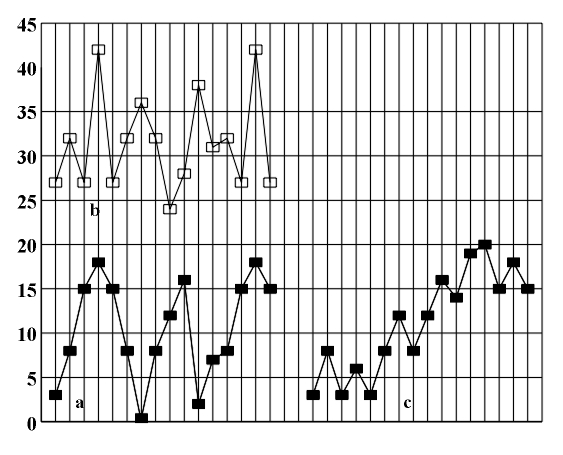
Each melodic line satisfies, in a greater or lesser degree, the principle of economy: the values of intervals between neighboring tones are within certain limits. If a sequence of intervals between neighboring tones i1, i2,...,in, corresponds to a melodic line, we call the sum of their values D=|i1|+|i2|+...+|in| the deviation of the melodic line. The deviation of the melodic line shows its deviation from a straight line parallel to the x-axis. In the case of the straight line that corresponds to the constant tonal pitch, the deviation equals zero. Deviation can be decreased if each tone of a melodic line is substituted with an adequately chosen same-name tone. Among all same-name melodic lines there will occur a melodic line with a minimum (least possible) deviation Dm. We will call this melodic line optimal (with the highest possible degree of economy) (Fig. 4.2). In order for a melodic line to be optimal, it is necessary for the values of all intervals between neighboring tones to be minimal. Finding a same-name minimum interval for the given interval i comes down to the following procedure:
In the previous chapter (p. 52) we classified intervals according to their sonority into consonant and dissonant. Note that in transition from any one interval to a same-name interval, the sonority of the interval does not change: consonant intervals become consonant, and dissonant intervals become dissonant. This means that the sonority of intervals is an invariant of this transition.
Figure 4.2 Different same-name melodic lines (a,b) and the optimal same-name melodic line (c).
|