|
Optimal conjoining of chords and simultaneous conducting of melodic lines
In the case of unison compositions, finding the optimal melodic line is very easy. However, with two-part and polyphonic pieces, we must conduct two or more melodic lines simultaneously, while each one of them must satisfy the principle of economy. In this chapter we will examine the counterpoint conducting of melodic lines while according to the principle of economy. Its basis is the optimal conjunction of tone pairs. Let us take two pairs of tones y1, y2 and y1', y2', i.e., the intervals i and i'. Our goal is to optimally conjoin them:
For example, let these pairs of tones be given: c1, e1 and d1, b1. Two conjunctions are possible:
In this way, the optimal conducting of two simultaneous melodic lines is reduced to optimal conjunctions of neighboring pairs of tones. This still does not mean that all key prerequisites for a counterpoint have been met. The next prerequisite is the elimination of parallel and anti-parallel movements, that can occur during conjunctions. With the first conjunction, parallel movement will occur if i11=i22 mod 12, and anti-parallel if i11+i22=0 mod 12. With the second conjunction parallel movement occurs if i12=i21 mod 12, and anti-parallel if i12=-i12 mod 12. In this situation we may avoid parallel movement or give priority to some other aspects (e.g., harmonic), opting for the closest to optimal conjunctions.
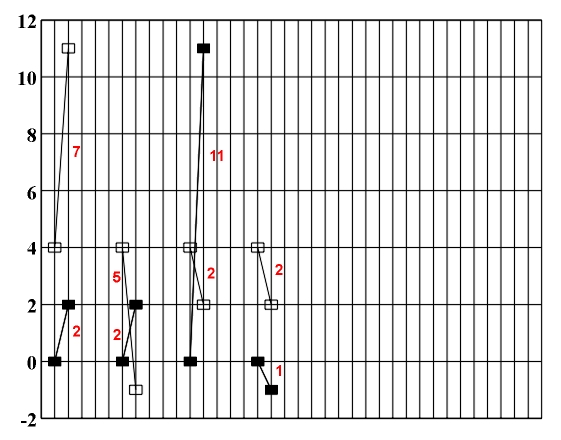
Figure 4.3 The conjunction of tone pairs C1, D1 and E1, B1. Conjunction (d) is optimal. The problem of conjoining pairs of tones, the elimination of parallel and anti-parallel movements, and the optimal conducting of counterpoint melodic lines may be very effectively solved by applying a simple computer program. In the case of polyphony, these problems are dealt with in an identical manner and require only the check of a large number of combinations - all possible conjunctions. Thus, when conjoining two triads, there are 6 combinations, the conjunction of two seventh-chords gives 24 combinations, and the conjunction of two ninth-chords gives 120 possible combinations. From all these combinations we choose the optimal ones. After that, by applying the same process as before, we look for the optimal conjunction, eliminate parallel and anti-parallel movements and resolve all related issues. To illustrate this we will show an algorithmic procedure which permits the optimal conjunction of two triads, regardless of whether they are incomplete triads (generated by doubling of one tone), full triads, the conjunction of a full triad with an incomplete one, or vice versa. Let us examine two triads y1,y2,y3 and y1',y2'y3', which give six possible conjunctions:
A visual scheme of all possible conjunctions is made by fixing the tones of the first triad, then permuting the tones of the second triad and finally conjoining them to the tones of the first triad (Fig. 4.4).
Figure 4.4 The schematic conjunction of two triads. The next step is reducing all intervals to same-name simple ascending intervals. After that, we will either keep the simple ascending intervals, or transform them into same-name complementary intervals, depending on whether they exceed or not the value of 6. Finally, we will calculate the sum of the obtained minimal intervals and find the optimal conjunction, i.e., the one which has the smallest sum of minimal intervals. After that we may verify whether parallel or anti-parallel movements occur with the chosen optimal conjunction. With some conjunctions parallel movements occur when any two intervals in a conjunction are equal modulo 12. In the event that unwanted parallel or anti-parallel movements do occur (e.g., parallel fifths or octaves), we will chose the conjunction closest to the optimal, i.e., the conjunction that corresponds to the next available value of minimal intervals. Likewise, it is possible to find the optimum conjunction of two five-note chords with or without a repeated tone. A scheme of 24 possible combinations of intervals of conjunction, obtained by fixing the tones of the first four-note-chord and their conjunction with the permuted tones of the second seventh-chord is shown in Fig. 4.5.
3 3 4 2 4 2 3 3 4 1 4 1 3 2 4 1 4 1 2 2 3 1 3 1 2 2 2 2 3 3 4 4 1 1 3 3 4 4 1 1 2 2 4 4 1 1 2 2 3 3 1 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 4 4
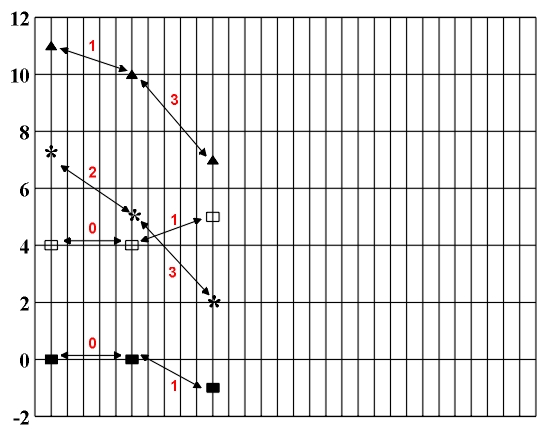
Determining a sequence of conjunctions of two triads or two seventh-chords, which begin with an optimal conjunction and decrease in economy, as well as the registering of parallel and anti-parallel movements, can be done very effectively by using a computer program. As an example we will show the optimal conjunction of a seventh-chord on the main notes of C major (T-S-D), made by the computer program (Fig. 4.6)
Figure 4.6 The optimal conjunction of a seventh-chords on the main notes of C major (T-S-D).
|