Symmetry transformations of polyphonic melody structure

 

From the aspect of symmetry analysis, the same symmetry transformations occur in the symmetry of counterpoint as in the symmetries of melodic structure, the only difference being that the former have an impact on the elements of one voice, transforming them into elements of a second voice. Without straying from the general subject we will examine only the symmetry analysis of two-part compositions. In this case the following analogous counterpoint isometric transformations occur:

1. transposition (translation t_x,y), or imitation (shift) (Fig. 4.7);

2. inversion (glide reflection g_x) (Fig. 4.8);

3. retrograde inversion (central reflection O), i.e., crab imitation (Fig. 4.9);

4. retrograde transposition (glide reflection g_y), i.e., the retrograde shift (Fig. 4.10).

 

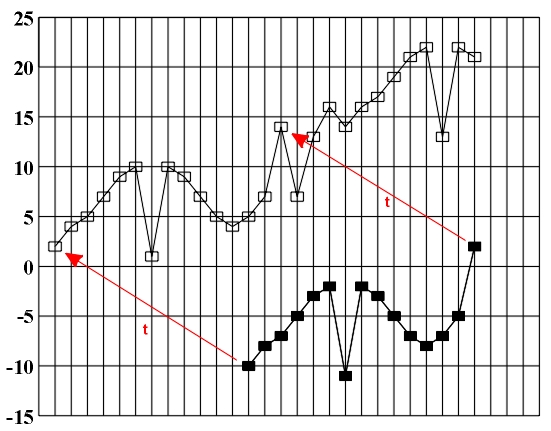
Figure 4.7 J. S. Bach, Two-part invention no. 4, an example of absolute imitation (translation t_x,y).

 

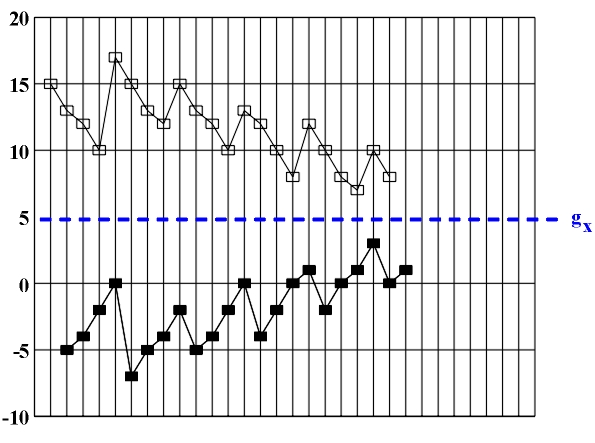
Figure 4.8 An example of inversion (glide reflection g_x) (M. Tajcevic: Kontrapunkt, example 450, p. 152).

 

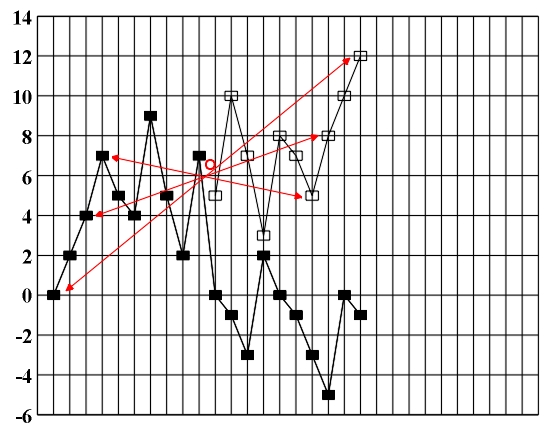
Figure 4.9 Crab imitation (central reflection O).

 

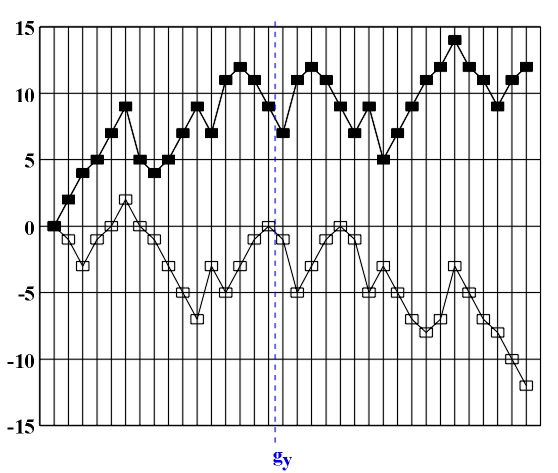
Figure 4.10 Retrograde shift (glide reflection g_y) (Musical Encyclopedia 2, 1963, p.481).

With this two specific new cases of the above mentioned transformations occur:

1. a) unison (parallel) imitation, i.e., translation t_y on the y-axis (Fig. 4.11), as a specific type of transposition;

2. a) anti-parallel imitation - mirror reflection m_x, whose axis is parallel to the x-axis. This is a special case of counterpoint inversion where the translation vector is equal to 0 (Fig. 4.12).

The first transformation (1a) brings about the appearance of a parallel melody, and the second (2a), the appearance of an anti-parallel melody in different voices.

 

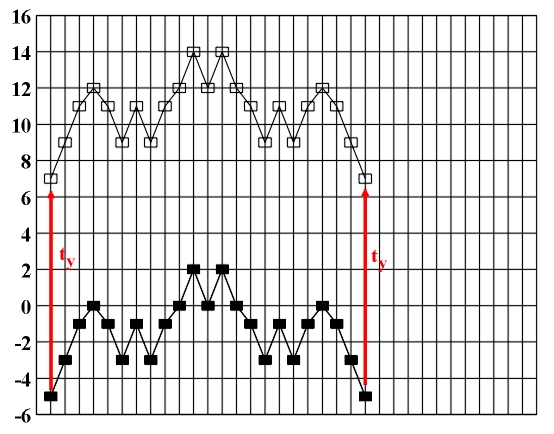
Figure 4.11 B. Bartok, Microcosmos, Vol. 1, Six Unison Melodies, part VI - an example of unison imitation (translation t_y) (Apagyi, 1989).

 

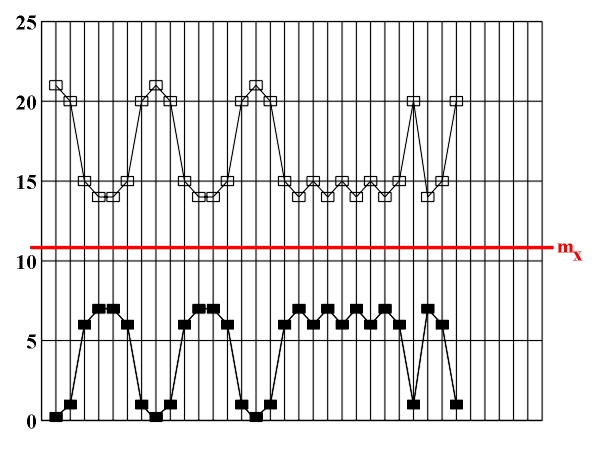
Figure 4.12 L. Papp, Leggiero. An example of anti-parallel imitation (mirror reflection m_x) (Apagyi, 1989).

The symmetry analysis of polyphonic pieces may be further expanded by a study of the counterpoint transformations of similarity, counterpoint permutation equivalence, etc. Different aspects of combining symmetry transformations of the rhythmic and melodic structures within counterpoint (e.g., counterpoint augmentation or diminishing) also occur.