|
Symmetry of harmonic functions
The symmetry analysis of the harmonic structure of a musical piece is based primarily on studying the symmetry of a sequence of harmonic functions. Besides that we will follow the harmonic flow, the sequence of the changes in stability. Both these properties become obvious only through the relationship between neighboring chords. For the purpose of a complete harmonic analysis, each fifth-chord must be assigned a set of relevant parameters:
We will denote the inversions of the fifth-chord with indexes 0,1,2, where index 0, which denotes the basic position, may be omitted. Seventh-chords may be studied in the same manner. Among the mentioned parameters, only the first two data may be registered directly. The third becomes accessible only after we have determined the tonality. However, each change in stability, i.e., the kinetic relationship of neighboring chords, is a property which can be identified in an auditory manner. The key places where these changes occur, and which may serve as referential points, are harmonic inversions and cadences. Two fifth chords with coefficients of stability s1 and s2 make a harmonic inversion if s1 < s2, i.e., s2-s1 > 0. The coefficient of the stability of an interval - the difference between the coefficients of stability of neighboring fifth-chords ks=s2-s1 will be the main indicator of the harmonic flow. For this reason we will study all possible harmonic inversions of two fifth-chords which occur in natural major and minor, harmonic minor and melodic minor. The following data are given for each harmonic inversion:
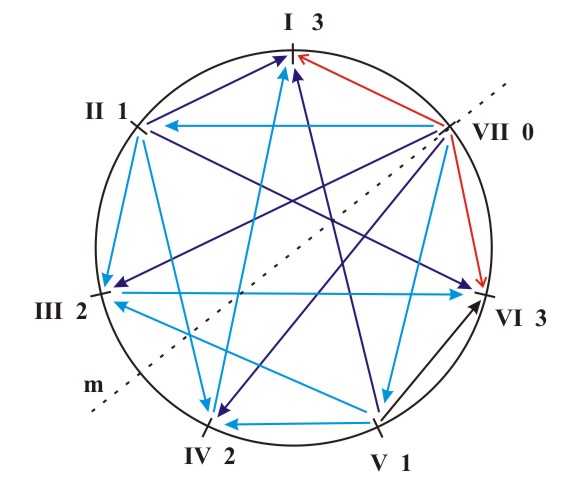
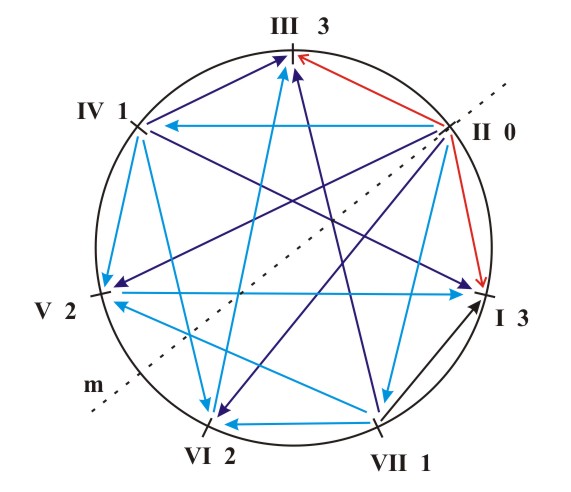
The results are illustrated with a diagram of the coefficients of stability of harmonic inversions (Figs. 5.6 and 5.7). The values ks=3,2,1 are marked with a thick, full and dotted line, respectively. A table of characteristic chord relationships and their functional interpretations also illustrates these results. This table will help us in the area of tonal orientation.
(a)
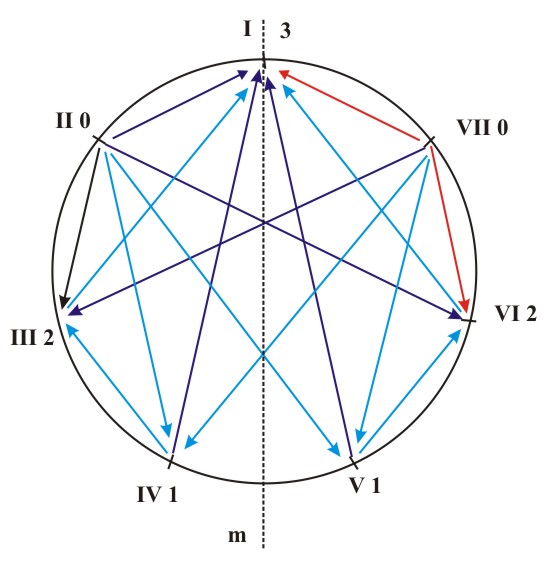
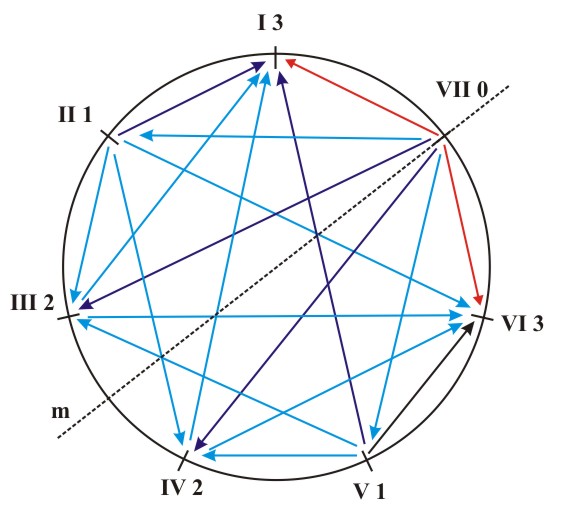
(b) Figure 5.6 A diagram of the coefficients of stability of harmonic inversions for natural major (a) and natural minor (b). From these diagrams we can deduce that the secondary tonic function of the VI degree in the major key will be more powerful than its secondary subdominant function, and that the secondary tonic function of the III degree in the natural minor will be more dominant than its secondary dominant function. As a result we get a symmetry diagram for the natural major and minor, with an axis of antisymmetry that contains the VII degree of the major key and the II degree of the minor key. This antisymmetry is responsible for preserving the tonic function (T-T, t-t) and it transforms the subdominant function into the dominant and vice versa (S-D, D-S, s-d, d-s) (Fig. 5.7).
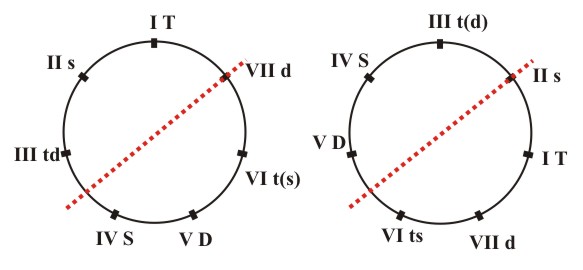
Figure 5.7 The axis of antisymmetry which corresponds to the transformation T-T, t-t, S-D, D-S, s-d, d-s in the major and natural minor. In case of the harmonic minor we get a mirror-symmetric diagram of the coefficients of stability of harmonic inversions. The axis of symmetry contains the tonic and runs between the subdominant and the dominant (Fig. 5.8a). Here is an accompanying table of the characteristic chord relationships and their functional interpretations:
For the melodic minor we get the following diagram (Fig. 5.8 b) and the accompanying table of the characteristic relationships between the chords and their functional interpretations:
(a) (b) Figure 5.8 A diagram of the coefficients of stability of the harmonic inversions for the harmonic minor (a) and melodic minor (b). Every harmonic inversion and every cadence of which it is part represents a stabilizing process. A cadence can be complete or incomplete, depending on whether all three harmonic functions or only two of them belong to it. The harmonic and melodic prerequisites for a perfect cadence are that the final harmonic inversion be of the type D-T or S-T, where both chords are in their basic position (which secures the fourth or fifth step in the bass, i=5,7), while the tonic chord is in the octave position. If some of the prerequisites (or the metric prerequisite) has not been met, the cadence is imperfect. Within a musical piece cadences can have the role of a specific "harmonic punctuation," as they act as a borderline between entities. Their intensity is determined by the degree of completeness of these entities. As an element of modulations, they are an affirmation of modulation and of a newly-established tonality, and the stabilization of a new tone center. The previous tables offer the possibility for a detailed analysis and registering of cadences, with the aim of tonal orientation. Two chords are balanced if their stability coefficients s1 and s2 are equal. By referring to the tables of the stability coefficients of chords we can easily identify balanced chords in the natural major and minor, harmonic minor and melodic minor, as well as all other relevant facts (as in the previous tables). Two chords with stability coefficients s1 and s2 are in the basic harmonic position if s1 > s2, i.e., if ks=s2-s1 < 0. Within the range of all studied tonalities, we may obtain the evidence of fifth-chords in the basic harmonic position directly from the tables of harmonic inversions. In doing so, the value of the intervals remains the same, while all other data is inverted. For example, in the first row of the first table.
is replaced with:
etc. As a result we get a survey of chord relationships, which allows us, after identifying the tonality, to determine the basic parameters relevant for the symmetry analysis of harmony. By assigning each chord the appropriate harmonic function (T,S,D,t,s,d) we get linear symmetry structures. In doing so we may resort to a rougher approximation and identify the secondary functions with the same principal ones, or we may conduct a more detailed analysis, differentiating between the main and the secondary functions. In both cases we get a linear structure which in the first instance can be described with 3-colored symmetry, and in the second instance, with 3-colored antisymmetry.
|