|
Extensions of tonalities by using isometric transformations of chords
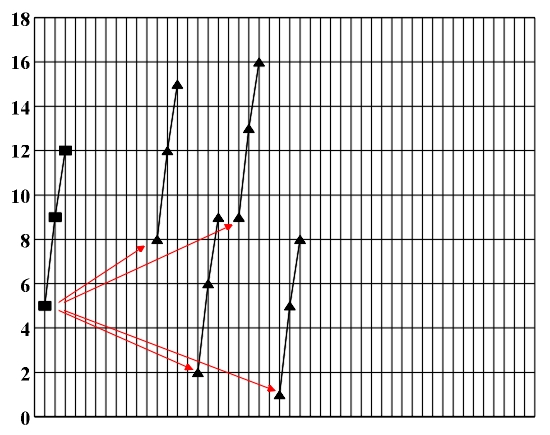
The next step is the extension of tonality. From the aspect of symmetry, this is the subjection of the chord structure of one scale to the action of isometric transformations, with the aim of transcending the scale and its chord structure. The first procedure to give us this result is the introduction of side subdominants and dominants. In the case of the major and natural minor (scales whose tonic, subdominant and dominant fifth-chord belong to the same type), the side subdominant of a chord is obtained by its transposition (translation) for the value of the interval i=5. The side subdominant of the fifth-chord y1, y2, y3 is the fifth-chord y1+5, y2+5, y3+5. If the fifth chord appears on the Nth degree of the scale (N=I,II,...,VII), we will denote its side subdominant as SN. For example, the side subdominant of fifth-chord 2,5,9 which is on the II degree of C major is the fifth-chord 7,10,14 which we will denote as SII. In a similar manner, the side subdominant DN of any fifth-chord on the Nth degree of the scale is obtained by its transposition (translation) for the value of the interval i=7 (Fig. 5.9). In practice, the side subdominant occurs most often in the form of a dominant seventh-chord (4,3,3) on the transposed initial tone (Fig. 5.9).
Figure 5.9 a) SVII of C major (S of D minor); b) DIII of C major (D of harmonic E minor). The real meaning of the side subdominant and side dominant is the forming of a harmonic inversion in which the side subdominant or dominant will take part, and the scale chord which will play the role of the local tonic. It is for this reason that the side subdominant and side dominant are deduced from consonant fifth-chords (maj, min) which have a tonic function in the natural major or minor tonality. Since the side subdominant and side dominant are deduced from the initial fifth-chord by a direct isometric transformation - transposition (translation), it is obvious that in this case the major fifth-chords are translated into major, and the minor into the minor. From the aspect of tonality extension, the side subdominants and side dominants are feasible only if by transposing them for the interval value of i=5,7 we transcend the limits of scale chords, which is most often the case. An exception in this case are the transpositions whose results are scale fifth-chords which belong to the initial scale:
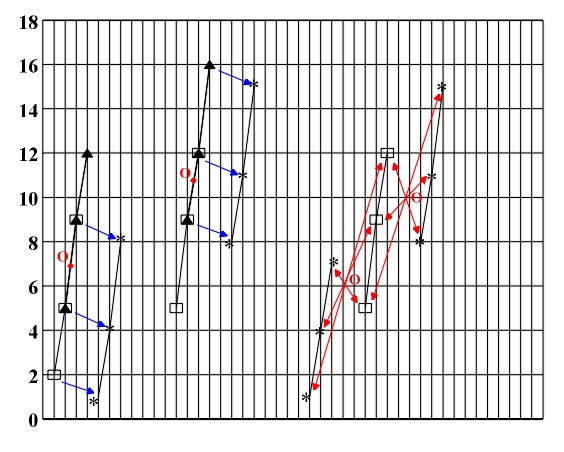
Another form of side chords stems from the relationship T-VII (maj - dim) in the major, or T-II in the minor. In the first case we assign a diminished fifth-chord y1+11, y2+10, y3+10 (VIIN) to a major fifth chord of our choice y1, 12, y3 which is positioned on the Nth degree of the scale. In the second case we assign a diminished fifth-chord y1+2, y2+2, y3+1 (IIN) to a minor fifth chord of our choice y1, y2, y3. For example, a major fifth chord 5,9,12 (F1-A1-C2) positioned on the IV degree of C major corresponds to the diminished fifth chord VIIIV: 16,19,22 (E2-G2-B2). The minor fifth-chord 2,5,9 (D1-F1-A1), positioned on the II degree of C major, corresponds to the diminished fifth-chord IIII: 4,7,10 (E1-G1-B1) (Fig. 5.10). The complete effect of the side VII and II degree is made possible in the harmonic inversion, where VIIN or IIN most often occurs in the form of a seventh-chord borrowed from the corresponding harmonic minor. Here we note the pronounced instability of the tritone rectangle (Fig. 5.4a).
Figure 5.10 a) VIIV of C major (VII degree of F major); b) IIII of C major (II degree of D minor). The III and VI degree of the natural major and minor will be the basis of a new transformation - the variant fifth-chord. From the point of view of symmetry, deriving a variant chord represents the retrograde inversion (central reflection) of the chord in respect to the middle tone. As variant chords are derived from the initial chord by retrograde inversion, major chords are transformed into minor ones and vice versa. It is possible to determine the variant fifth-chord Nv(min,maj) for every consonant fifth-chord (maj,min) on the Nth degree of a scale. Any asymmetric (consonant) fifth-chord (maj, min) can serve as the basis for building the variant fifth-chord, as centrally symmetric (dissonant) fifth-chords (dim, aug) are translated into themselves by the said central reflection (Fig. 3.11). For the major fifth-chord y1, y2, y3 the variant fifth-chord is y1+1, y2, y3+1, whereas for the minor fifth-chord y1, y2, y3 the variant fifth-chord is y1-1, y2, y3-1. For example, the variant fifth-chord IIIv of the minor fifth-chord 4,7,11 (E1-G1-B1) which is positioned on the II degree of the C major scale, is the major fifth-chord 3,7,10 (E-flat 1,G1-B-flat 1), whereas the variant fifth-chord of VIv of the major fifth-chord 8,12,15 (A-flat 1-C2-E-flat 2) on the VI degree of C minor, is the minor fifth-chord 9,12,16 (A1-C2-E2) (Fig. 5.11).
Figure 5.11 a) IIIv of C major; b) VIv of C minor, a result of retrograde inversion (central reflection) in respect to the middle tone. The reduction of intervals to minimal same-name intervals has shown that interval i=6 is the maximum reduced interval. The consonant chord PN, derived by transposition (translation) of its initial tone for the value of interval i=6 from a consonant chord on the Nth degree of a scale, is called the polar chord. For example, polar chord PIII of the minor chord 4,7,11 (E1-G1-B1) on the III degree of C major, is the minor chord 10,13,17 (B-flat1-D-flat 2-F2) (PIII), or the major chord 10,14,17 (B-flat1-D2-F2). The next extension of tonality is obtained by the application of different forms of relationship between keys a third apart. From the aspect of the theory of symmetry, the diatonic relationship between keys that are a third apart represents retrograde inversion (central reflection) in respect to the center of one of the intervals of the third which form part of a fifth-chord. The mentioned retrograde inversion transforms the major fifth-chord into a minor one and vice versa, a diminished one into a diminished one, and an augmented one into an augmented one. Since we are dealing with retrograde inversion in respect to the center of the interval of the third which forms part of a fifth-chord, its extreme tones remain preserved. For this reason, every two diatonically related fifth-chords share two common tones each. Because we use two centers of reflection for deriving diatonically related thirds from a given fifth-chord, each fifth-chord has two diatonically related thirds. If the initial fifth-chord y1, y2, y3 is major, minor or diminished, its diatonic third relatives are, respectively: y3-10, y1, y2 and y2, y3, y1+11 (min), y3-11, y1, y2 and y2, y3, y1+10 (maj), y3-9, y1, y2 and y2, y3, y1+9 (dim). For example, the diatonic relatives of the major fifth-chord 5,9,12 (F1-A1-C2) are the minor fifth chords 2,5,9 (D1-F1-A1) and 9,12,16 (A1-C2-E2); the diatonic relatives of the minor fifth-chord 4,7,11 (E1-G1-B1) are the major fifth-chords 0,4,7 (C1-E1-G1) and 7,11,14 (G1-B1-D2), and the diatonic relatives of the diminished fifth-chord 11,14,17 (B1-D2-F2) are the diminished fifth-chords 8,11,14 (G-sharp 1-B1-D2) and 14,17,20 (D2,F2,A-flat 2) (Fig. 5.12). The concept of the diatonic relative of an augmented fifth-chord is pointless, since the result of this are its inversions y3-12, y1, y2 and y2, y3, y1+12. Figure 5.12 Diatonic relatives, a result of retrograde inversion (central reflection) in respect to the center of the interval of the third. A chromatic relationship between keys a third apart is based on the upwards or downwards transposition (translation) of the given fifth-chord, for the interval of the third i=3,4. We get four chromatic third relatives from the fifth-chord y1, y2, y3:
They belong to the same type as the initial fifth-chord. Since the value of the translation vector equals 3 or 4, each chromatic third relative shares one common tone with the initial fifth-chord. For example, from the major fifth-chord 5,9,12 (F1-A1-C2) we get four chromatic third relatives:
Figure 5.13. Chromatic third relatives as a result of transposition (translation). There is no point in speaking about chromatic relationships between keys a third apart in the context of diminished and augmented fifth-chords, since for the diminished fifth-chord and the transposition interval i=3 and for the augmented fifth-chord and transposition interval i=4 we get diatonic relatives. For the diminished fifth-chord and transposition interval i=4 and for the augmented fifth-chord with a transposition interval of i=3 we get only apparent third relatives. An apparent relationship between keys a third apart is easiest to describe by means of a composition of isometric transformations - the transposition (translation) of diatonic relatives of a major fifth-chord for the interval i=-1 and the transposition (translation) of diatonic relatives of a minor fifth-chord for the interval i=1. Knowing that the composition of the retrograde inversion (central reflection) and transposition (translation) is a new retrograde inversion (central reflection), we may conclude that the apparent third relatives may be obtained directly from the initial fifth-chord by using retrograde inversion (central reflection). It follows that each apparent third relative of a major fifth-chord is a minor fifth-chord and vice versa. Depending on whether the initial fifth-chord y1, y2, y3 is a major or a minor one, we get its apparent third relatives respectively: minor fifth-chords y3-11, y1-1, y2-1 and y2-1, y3-1, y1+10 or major fifth-chords y3-10, y1+1, y2+1 and y2+1, y3+1, y1+11. For example, for the major fifth chord 5,9,12 (F1-A1-C2) the apparent third relatives are the minor fifth-chord 1,4,8 (C-sharp 1-E1-G-sharp 1) and 8,11,15 (G-sharp 1-B1-D-sharp 2) (Fig. 5.14). For the minor fifth-chord 4,7,11 (E1-G1-B1) the apparent third relatives are the major fifth-chords 1,5,8 (C-sharp 1-E-sharp 1-G-sharp 1) and 8,12,15 (G-sharp 1-B-sharp 1-D-sharp 2). Figure 5.14 Apparent relationships between keys a third apart as a result of retrograde inversion (central reflection). The mentioned forms of relationships between thirds represent the basis of mediantics - the use of diatonic, chromatic, or apparent relationships of the main degrees as their representatives. All the studied transformations of chords are carried out by way of two isometric transformations: transposition (translation) and retrograde inversion (central reflection). Transposition preserves the type of chord and retrograde inversion inverts it: it transforms the major fifth-chord (4,3) into the minor (3,4) and vice versa.
|