|
Symmetry of seventh-chord structure of scales
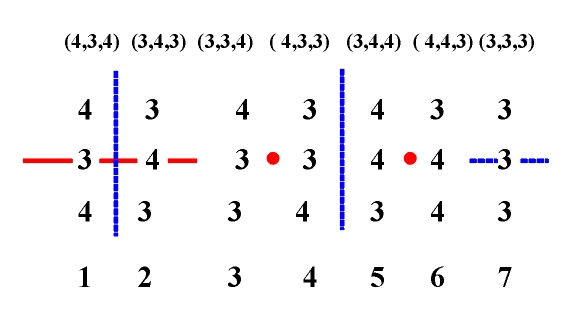
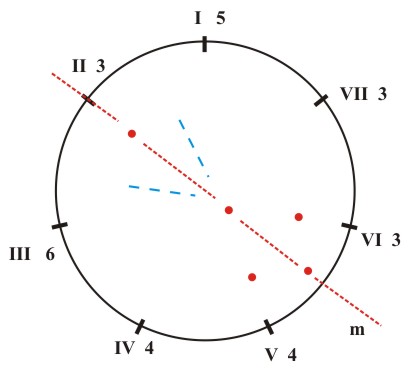
While examining the symmetry of scales we mentioned the axis of antireflection which contains the VII degree in the major scale and the II degree in the minor scale (Fig. 5.3) which also inverts the fifth-chords. The symmetry of the fifth-chord structure encourages an analogous study of the seventh-chord structure of scales with the aim of finding its symmetry. For this reason we will denote the seventh chords in the following manner:
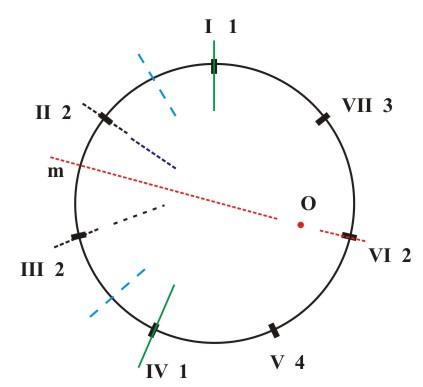
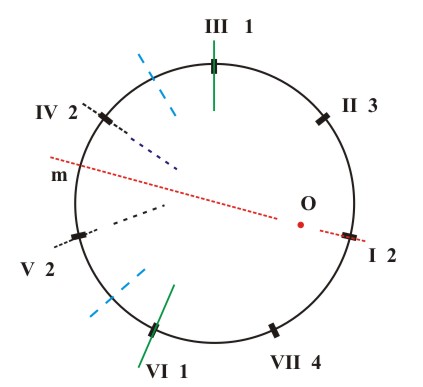
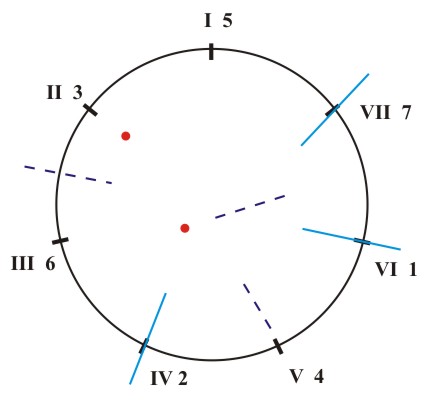
The elements of the symmetry of the seventh-chords themselves and the elements of symmetry that link individual seventh-chords or groups of seventh-chords are shown in the following manner: mirror reflections (m) are marked with thick lines (axes of reflection), mirror antireflections which translate minor thirds (i=3) into major thirds (i=4) and vice versa, are marked with broken lines (axes of antireflection) and central reflections (O) (retrograde inversions) with points (centers of reflection). We can read the table of the seventh-chord structure of major, natural minor, harmonic minor and melodic minor scales directly from the corresponding diagrams of interval structure (Figs. 5.2; 5.4). The table is as follows:
(a)
(b)
(c)
(d) Figure 5.15 The symmetry of the seventh-chord structure of the major key (a), the natural minor (b), the harmonic minor (c) and the melodic minor (d).
|