|
Symmetry of chromatic seventh-chords
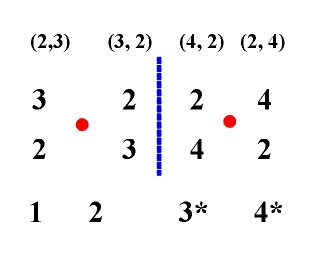
The specific approach to chromatic chords in this thesis follows from the definition of interval i. The interval is defined as the difference between the tonal pitches of the end tone y2 and the initial tone y1 (i=y2-y1), not as the function of its place in the scale (the degree on which the end and initial tones are positioned). Another reason for this specific approach is the identification of enharmonic tones: C-sharp = D-flat , D-sharp = E-flat , E = F-flat , E-sharp = F, F-sharp = G-flat , G-sharp = A-flat , A-sharp = B-flat , B=C-flat , B-sharp = C. From the point of view of intervals, this leads us to the identification of each chromatic interval with the corresponding diatonic interval which can be obtained by enharmonic exchange. This means that each interval will occur in a scale as a diatonic interval, i.e., an interval made up by two scale tones. In our study of chords we started out by combining intervals with values i=3,4 (minor and major thirds). By using this criterion no other prerequisites are necessary for determining scale chords, the only exception being the VI degree of the harmonic minor in which we opt for the interval i=4, made up by non-neighboring tones A-flat1 and C2, not for interval i=3, made up by neighboring tones A-flat 1 and B1. Since the essence of chromatics is based on the occurrence of the diminished third (the dissonant interval i=2) within chords, we may consider that a chromatic chord is a chord (i.e., a numerical sequence of tonal pitches) consisting of one dissonant interval i=2 and other consonant intervals i=3,4. In the case of chromatic fifth-chords there are four possibilities which correspond to a chord with diminished third and doubly diminished fifth (2,3), to a chord of minor third and doubly diminished fifth (3,2), to a major triad with a diminished fifth (4.2), and to a chord of a diminished third and a diminished fifth (2,4). This is presented in the following table along with the corresponding symmetry transformations:
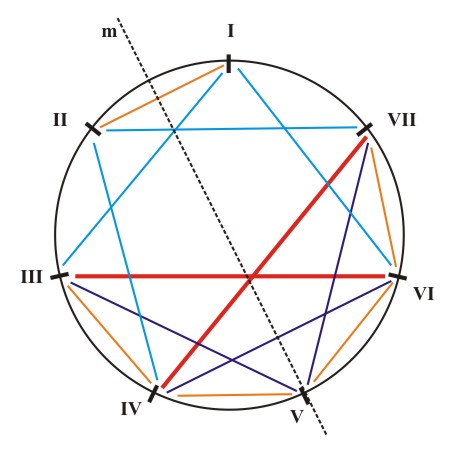
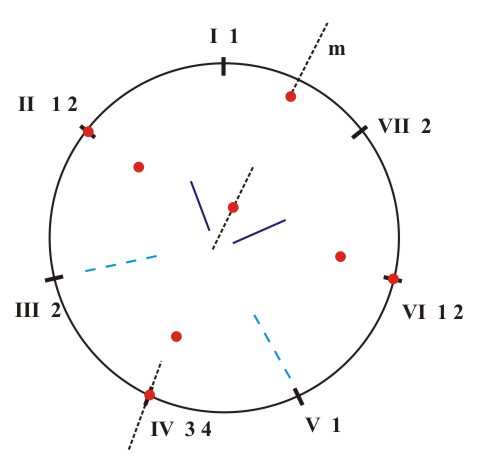
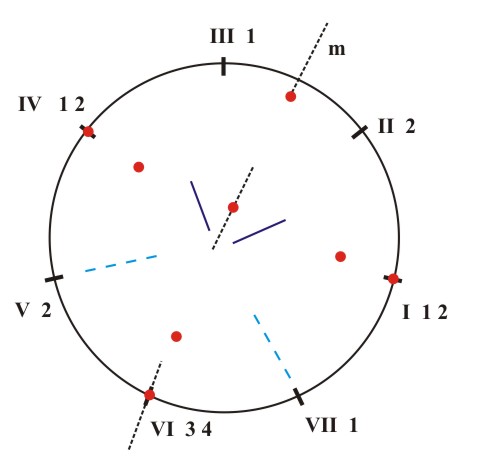
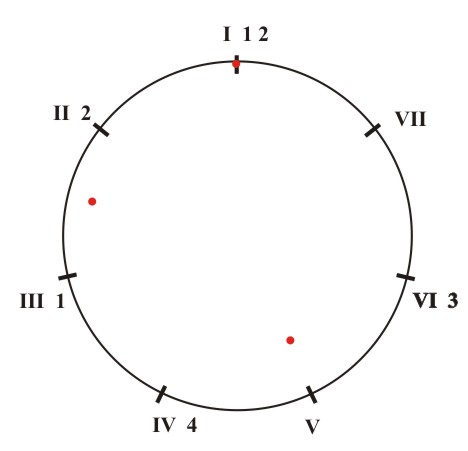
We note that besides the dissonant interval i=2, the major triad with a diminished fifth (3) and the chord of a diminished third and a diminished fifth (4) contain the dissonant tritone interval i=6, for which reason they have been marked with an asterisk. Our next task is to register the appearance of corresponding sequences of tonal pitches which correspond to the mentioned chromatic fifth-chords in different scales. The diagrams of the interval structures of the major, natural minor, harmonic minor and melodic minor tones offer insight as to this task. In these diagrams the intervals i=4 are marked with a full line, the intervals i=3 with a broken line and the intervals i=2 with a dotted line (Fig. 5.16). For example, on the I degree of the major key there is a chord with a diminished third and a doubly diminished fifth (2,3) (1) and on the II degree of the major key there is a chord with diminished third and doubly diminished fifth (2,3) (1) and a chord of a minor third and a doubly diminished fifth (3,2) (2), etc. In this manner we get a table of the distribution of chromatic fifth-chords in the major, natural minor, the harmonic minor and the melodic minor keys with the accompanying diagrams (Fig. 5.17):
(a)
(b)
(c)
(d) Figure 5.16 The distribution of intervals i=4 (), i=3 (- - - -), i=2 (....) in the major (a), the natural minor (b), the harmonic minor (c) and melodic minor (d).
(a)
(b)
(c)
(d)
|