|
Dynamic symmetry and golden section
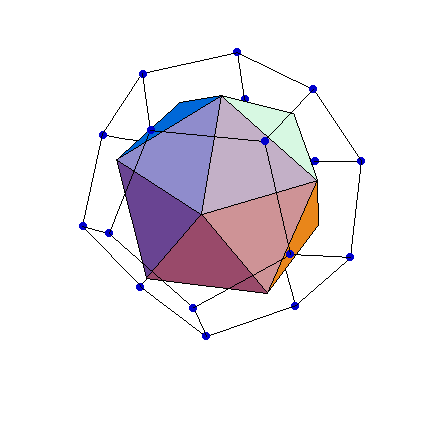
In contrast to static symmetry, i.e., the symmetry of equilibrium (balance), dynamic symmetry (division based on the golden section), is the perfect form of asymmetry. According to the theory of perception, there are two optimal possibilities of a harmonic division of a whole: mirror reflection (symmetric division) and a division based on the golden section (an asymmetric division, where the ratio of the lesser part to the greater is the same as the ratio of the greater to the whole). Dynamic symmetry characterizes live matter as opposed to static symmetry which is predominant in the world of crystals. The golden section (sectio aurea, or de divina proportione, according to L. Paccioli (Coxeter, 1961, p. 162) j = [(Ö5-1)/2] ~ 0,618... is the positive root of the quadratic equation j2+j -1=0, i.e., the division of a unit line segment into two parts so that the ratio of the smaller part to the greater is the same as that of the greater to the whole line segment (Fig. 7.17).
Figure 7.17. Construction of the regular pentagon, the golden section j = [(Ö5-1)/2], regular dodecahedron and icosahedron. The dynamic characteristics of the golden section stem from the fact that it represents the basis for the construction of a regular pentagon, icosahedron and dodecahedron - regular polygons and polyhedra that are out of the domain of crystallographic periodic structures, since they fail to completely fill a plane or space, but which very often occur as forms of symmetry in the living world (star-fish, flowers and fruits, etc.) (Fig. 7.18). The golden section is connected to Fibonacci's sequence 1,1,2,3,5,8,13... defined by the recursive formula f1=1, f2=1, fn+fn+1=fn+2, whose quotients of consecutive elements [(fn)/(fn+1)] (1/1, 1/2, 2/3, 3/5, 5/8, 8/13...) give an approximation of the golden mean (the number t) (Coxeter, 1961, p. 165). This sequence appears in nature, in phyllotaxis - the most favorable arrangement of leaves on a plant for optimized access to sunlight which occurs according to Fibonacci numbers (Coxeter, 1961, p. 169). In a most general sense, the golden section is the ideal form of proportionality: the distribution of objects while preserving proportionality, i.e., similarity between the parts and the original object (so-called self-similarity). In the living world it is related to the process of growth - a proportional increase while preserving the shape by means of similarity that often characterizes spiral forms (the Nautilus shell, the spiral seed pattern of a sunflower, the fruit of the pineapple,...) (Fig 7.19). (a)
(b)
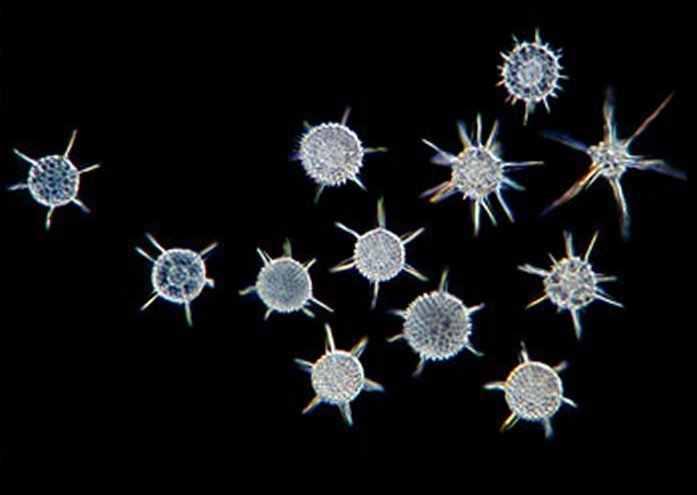
(c) Figure 7.18 The pentagonal symmetry of a flower (a) and sea star (b), and radiolaria (c).
Figure 7.19 A sea shell, logarithmic spiral and gnomonic growth. In visual arts and architecture, the golden section is the dynamic bearer of harmony (Fig. 7.20).
Figure 7.20 Gothic plans based on the golden section, i.e., the symmetry of the regular dodecahedron. Within the range of the symmetry of form in the thematic plane, dynamic symmetry is characterized by the transitional form of the binary form a-a-b-a, the five-part form a-b-a-c-a, the rondo A-B-A-C-A, or the rondo in the Violin Concerto K.V. 216 in G major by W. A. Mozart A-B-A-B-A-C-D-A-B-A. It plays a much more significant role in the tonal and structural plane where almost all of the important changes (local or global culminations, modulation points, etc.) coincide with the golden section points in musical pieces. Each culmination point is accompanied by a change in the symmetry of the melody, harmony and dynamics. For example, according to M. Apagyi's research (1989), in the first part of Microcosmos by B. Bartok the culmination points (melody culminations) coincide with the left and right point of the golden section (Fig. 7.21).
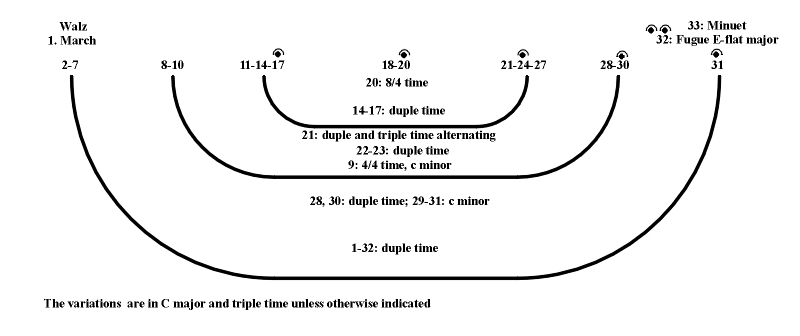
Figure 7.21. The points of the golden section as the points of melodic culmination (B. Bartok, Microcosmos 1) (Apagyi, 1989). In the thematic and tonal plane of Beethoven's Thirty-three Variations of a Waltz by A. Diabelli, op. 120, the transition to a [6/4] measure occurs in the 20th variation, i.e., in the right point of the golden section ([20/33] ~ 0,61...) (Fig. 7.22). Although the culmination (marked with a + sign) may coincide with the center (Fig. 7.23), it most often coincides with the right point of the golden section: it is located in the accentuated part of the sixth measure in an eight-measure melody (Fig. 7.24), in the accentuated part of the 11th measure in a sixteen-measure melody, or in the accentuated part of the 21st measure in a 32-measure melody (Mazel, 1979, p. 92). In all these cases the ratio 5:3=10:6=20:12 approximately corresponds to the value of the golden mean. In this manner, within quadratic structures with 2n measures (Holopova, 1974, p.74) that allow for a regular division in 4 measure phrases, we note the appearance of a specific balance of the static (quadratic and 4-measure phrase periodicity) and the dynamic components (golden section). Figure 7.22 (Lemacher and Schroeder, 1967).
Figure 7.23 P. I. Tschaikovsky, La Damme Piquee (Mazel and Zuckerman, 1967).
Figure 7.24 L. van Beethoven, Piano Sonata no. 16 (Mazel, 1979). In F. Chopin's Prelude 1 the point of the golden section coincides with the melodic and dynamic culmination, expressed by the number of measures (Fig. 7.25). The dynamic fortissimo and the melodic culmination in the 21st measure marks the division of Prelude 1 which consists of 34 measures in a ratio of 21:34 ~ 0,6176... according to the golden section. We also come across the application of dynamic symmetry in music pieces whose thematic plane at first site seems to be based on static symmetry.
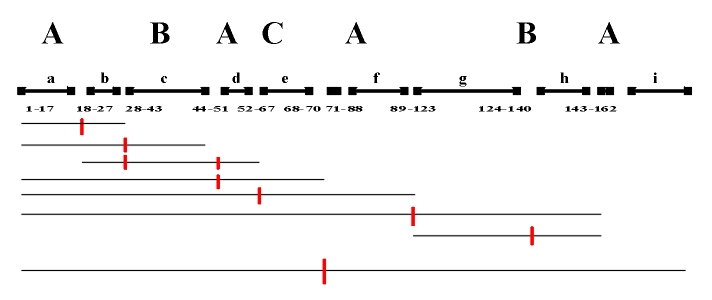
However, it is only after registering the structural plane, i.e., the number of measures that correspond to individual thematic entities, that we discern the role of dynamic symmetry. As an illustrative example we will cite the third movement of W.A. Mozart's Piano Sonata in B major, K.V. 281. The asymmetric tonal plane B-F-B-G minor-B-B-B corresponds to the thematic plane based on the static symmetry of the sonata rondo form A-B-A-C-A-B-A. The dynamic symmetry upon which this piece is based is fully recognizable only after a structural analysis of the thematic and tonal plane. In this process we can identify the occurrence of the following entities: a) the first theme in B-flat major (1-17 measure); b) modulatory transition into F major (measure 8-27); c) second theme (measure 28-43); d) second occurrence of the first theme (measure 44-51); e) third theme in G minor (measure 52-67) and the modulatory transition into the initial tonality (measure 68-70); f) third occurrence of the first theme (measure 71-88); g) developed transition from first theme to second theme (measure 89-123); h) second occurrence of second theme (measure 124-140) followed by a brief transition (measure 140-142); i) fourth occurrence of first theme (measure 143-162) (Skovran and Pericic, 1986). In the accompanying diagram we show the points which correspond approximately to the golden section and which coincide with the significant points of the thematic and tonal plane of the composition (Fig. 7.26).
A very indicative example of the construction of a musical piece based on the principle of Fibonacci's sequence is the introduction (measure 21) of F. Chopin's Etude in E major, op. 10, no. 3 (Fig. 7.27). It is based on a sequence of proportions 2:3:5:8:13:21 (Holopova, 1974, p. 99). In a similar way, the rhythmic series from the second movement of L. Nono's cantata Il Canto Sospesso is based on Fibonacci's sequence (Holopova, 1974, p. 99).
Figure 7.27 F. Chopin, Etude in E major, op. 10, no. 3 (Holopova, 1974). Fibonacci's sequence, in which each element is equal to the value of the sum total of the two preceding elements, represents a specific case of more general structures, addition structures, in which every element is the sum of its precedents (or sequels). The following examples of ascending progressive summing of quadratic structures are found in a variety of musical works, particularly with F. Chopin: double summing 1+1+2+4 within a two-phrase measure, triple summing 1+1+2+4+8 (or 1/2+1/2+1+2+4), and quadruple summing 1/2+1/2+1+2+4+8 (Fig. 7.28), or descending double summing 4+2+1+1 (Mazel and Zuckerman, 1967) (Fig. 7.29). Ascending and descending progressive summing, as well as related structures based on proportional distribution 4+4+2+2+1+1+(2) (Figs. 7.30-7.31) represent a way of transcending literal (translational) periodicity and the establishing of proportional regularity in quadratic structures (Mazel and Zuckerman, 1967).
Figure 7.28 F. Chopin, Prelude in G major (Mazel and Zuckerman, 1967).
Figure 7.29 F. Chopin, Mazurka, op. 6, no. 3 (Mazel and Zuckerman, 1967).
Figure 7.30 C. Saint-Saëns, Samson and Delilah (Mazel, 1979).
Figure 7.31 F. Schubert, Impromptu in A-flat major, op. 90, no. 4 (Mazel and Zuckerman, 1967). Since the identification of symmetries which characterize only the thematic or tonal plane is insufficient for a conclusive study on the symmetry of form, the research of the symmetry of form in fact solves the problem of the correlation of symmetry structures carried out in the structural plane, i.e., by the introduction of common metrics (the number of measures) that allows a simultaneous symmetry analysis of the thematic and tonal plane. We must resort to a similar procedure in the further symmetry study of a musical piece, identifying the correlation between the different symmetry structures (rhythmic, melodic, harmonic, etc.) first on a local, then on a global level.
|