The symmetry analysis of musical work

 

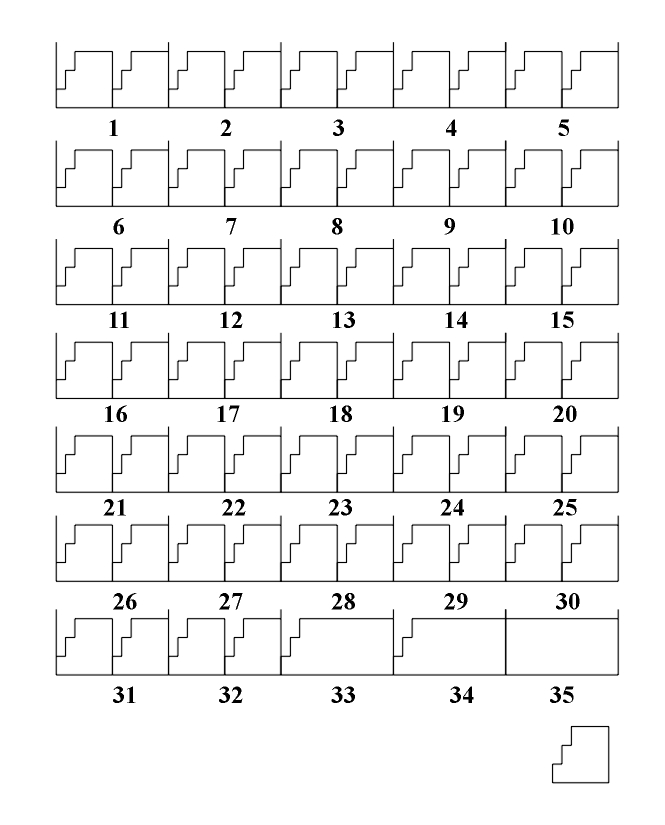
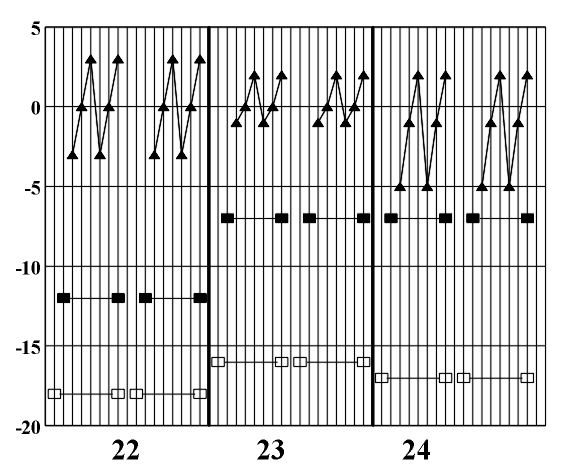
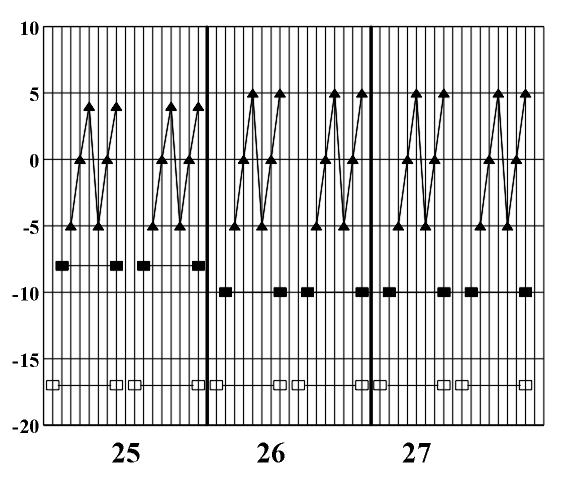
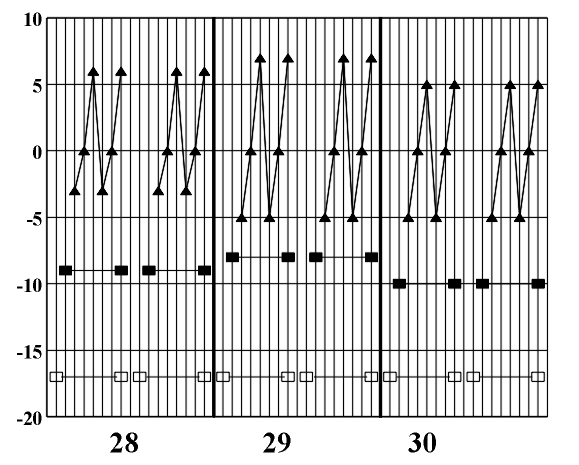
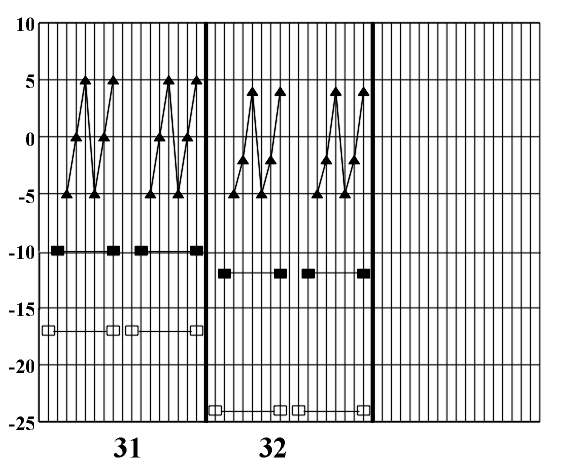
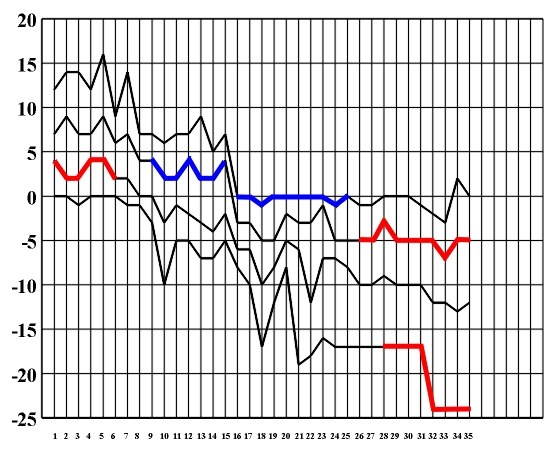
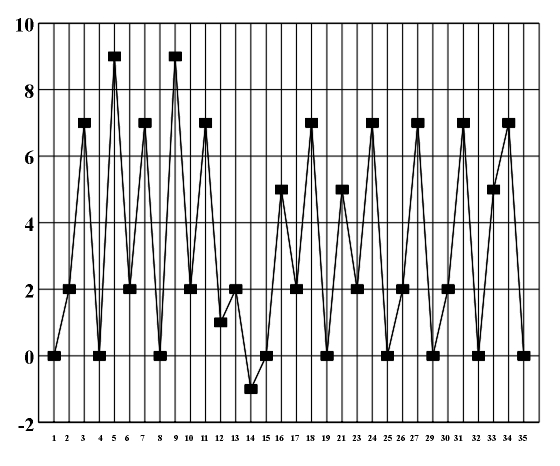
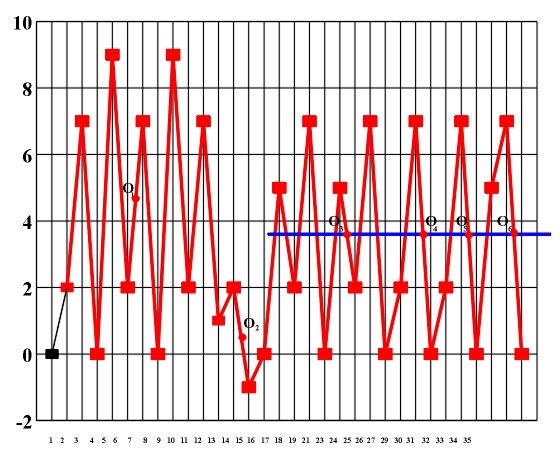
The theoretic study and the formalization of musical language which was dealt with in previous chapters represents the basics for the symmetry analysis of a musical piece. As an example we will present the symmetry analysis of J. S. Bach's Prelude no. 1 in C major from the Well-tempered Piano (Fig. 8.1).

Figure 8.1 J.S. Bach, Prelude no. 1 in C major (Vinogradov and Krasovskaya, 1991).

Its rhythmic structure is strictly regular and represents a symmetric linear translational structure based on the literal repetition of an asymmetric rhythmic model (Fig. 8.2). It satisfies global symmetry and, in the sense of the symmetry of friezes, it corresponds to the symmetry group p1 (Fig. 8.2b).

(a)

(b)

Figure 8.2 An elementary asymmetric rhythmic model (a) and a symmetric diagram of a rhythmic structure (b).

Out of 35 measures that make up this musical piece, the initial rhythmic element is literally repeated in each measure two times in the first 32 measures. The last three measures show the process of symmetrization - evolutive transformation which, by means of linking two initial asymmetric rhythmic models (measures 33, 34), leads to complete symmetrization (measure 35).

Since there is a high correlation level between the symmetry of the rhythmic and melodic-harmonic structure, instead of constructing individual symmetry diagrams, the studied piece allows the construction of a common diagram. This diagram presents at the same time the symmetry of the rhythmic and melodic-harmonic structure and facilitates their simultaneous study (Fig. 8.3).

 

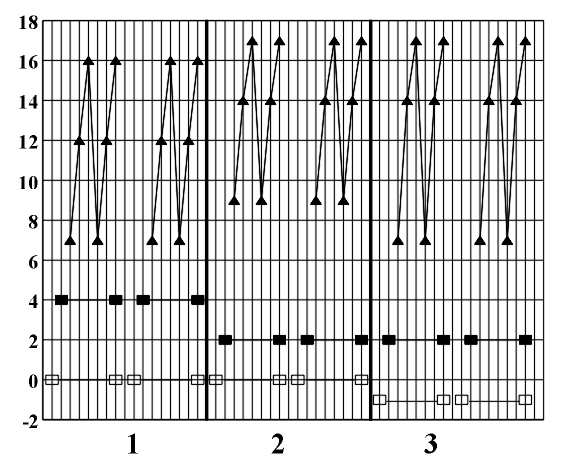
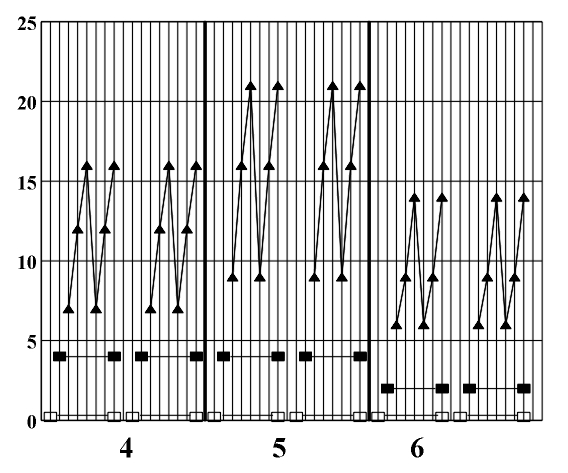
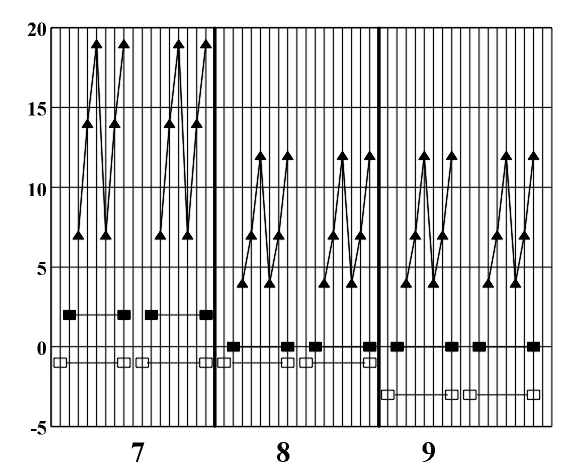
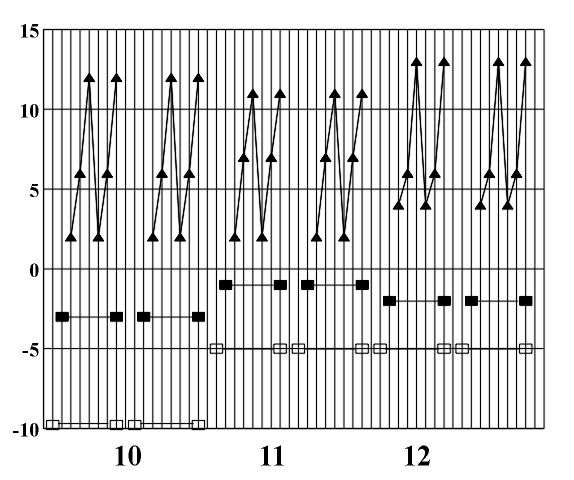
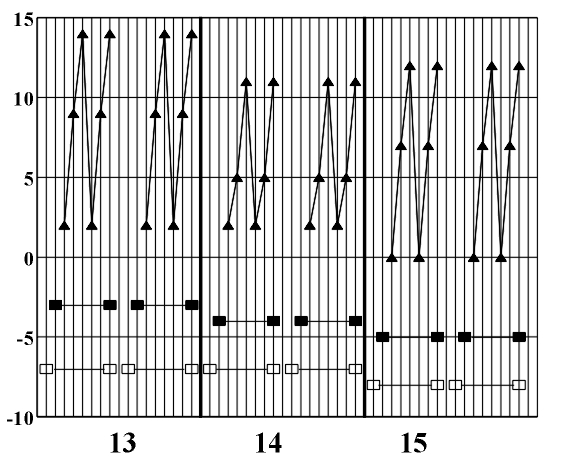
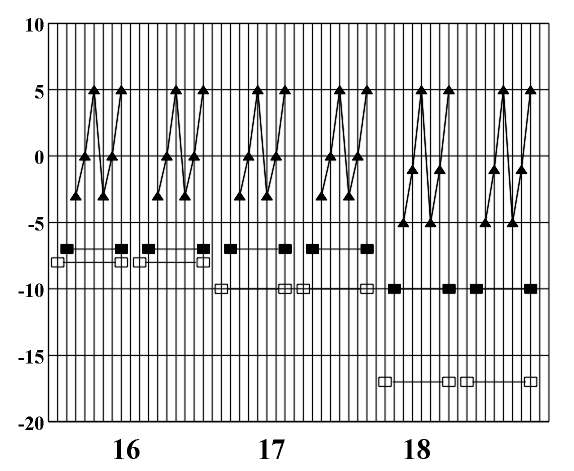
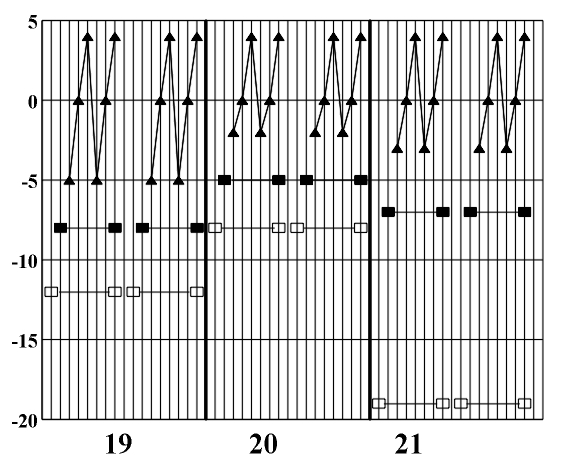
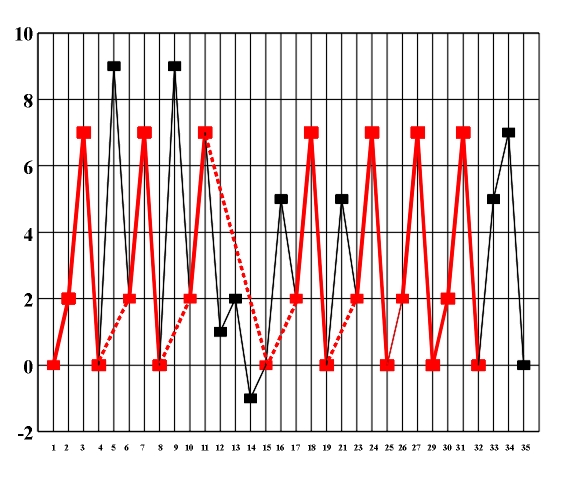
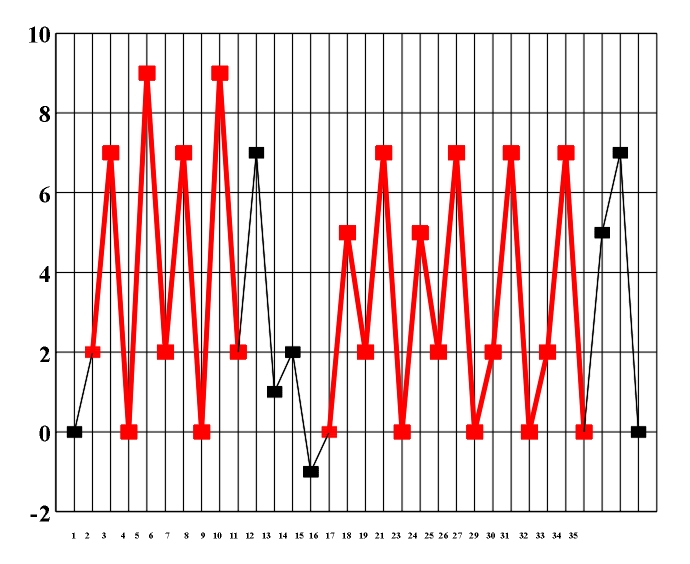
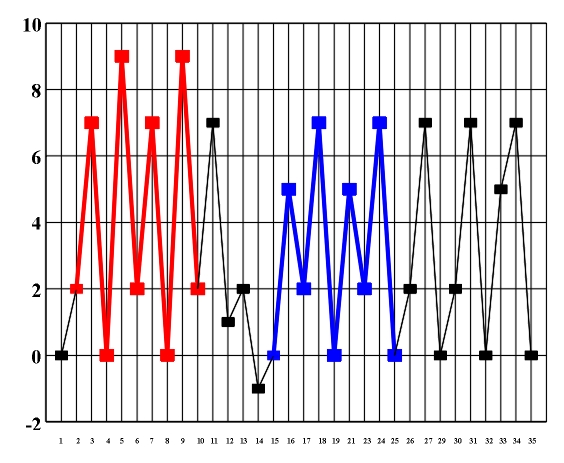
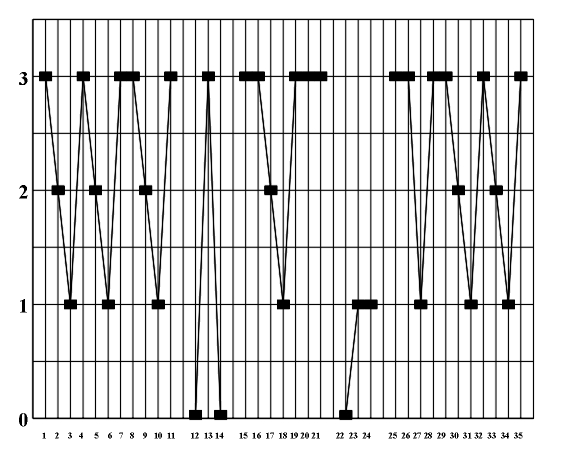
Figure 8.3 A diagram of the symmetry of rhythmic and melodic structure.

By applying horizontal analytic reduction, we get a diagram of the counterpoint structure (Fig. 8.4) on which individual forms of local symmetry are shown). The local symmetries that appear here are retrograde inversion (central symmetry O) and retrograde repetition (mirror reflection m_y) (Figs. 3.16 - 3.17).

Figure 8.4. A diagram of the symmetry of counterpoint structure.

After range and doubling reduction we gain insight into the chord structure of the piece (Fig. 8.5) which is the basis for the symmetry analysis of harmony.

Minor tonalities are denoted by small letters, and the altered chords are marked with an asterisk.

	12	17			12		11	19	12		10
7	9	14	7	16	9	14	7	16	9	14	7
4	5	11	4	12	6	11	4	12	6	11	4
0	2	7	0	9	2	7	0	9	2	7	1
1	2	3	4	5	6	7	8	9	10	11	12
CI	CII	CV	CI	CVI	GV	GI	GIV	GII	GV	GI	dVII
				(GII)						(dIV)

	8		16	12	17		10	16	12	12	17
9	5	7	12	9	14	7	7	12	9	8	14
5	2	4	9	5	11	4	4	9	6	5	11
2	-1	0	5	2	7	0	0	5	3	2	7
13	14	15	16	17	18	19	20	21	22	23	24
dI	CVII	CI	CIV	CII	CV	CI	CI*	CIV	CII*	cII*	CV
(CII)

			9
	12	17	7		12	17	10		17
7	7	14	6	7	7	14	7	12	14	7
4	5	11	3	4	5	11	4	9	11	2
0	2	7	0	0	2	7	0	5	7	0
25	26	27	28	29	30	31	32	33	34	35
CI	CII*	CV	CII*	CI	CII*	CV	CI*	CIV	CV	CI

Figure 8.5 The chord and harmony structure.

If each chord is represented by its basic tone, the result we get is a diagram of the symmetry of the harmonic structure (Fig. 8.6). In this diagram we can directly note the literal repetition of the harmonic sequence II-V-I, that is, the sequence I-II-V-I which, because of its significance in this piece, plays the role of the idea. In the following diagrams we will present the symmetry of harmonic structure based on literal repetition (translation t_x) (Fig. 8.7a) and retrograde inversion (central reflection O) (Fig. 8.7b). Here we also note the regularity of the arrangement of the centers of central reflections - the collinearity of the points O₃, O₄, O₅, O₆. Finally, the specific non-isometric symmetry (Fig. 8.7c) occurs between the entities. The first entity is transformed into a second by retrograde transposition (glide reflection g_y), accompanied by a substitution of all intervals by complementary intervals (interval 7 by interval 5, interval 9 by interval 3).

(a)

(b)

Figure 8.6 A diagram of the symmetry of harmonic structure (a) based on the harmonic sequence I-II-V-I.

 

As a result of assigning adequate main or secondary harmonic functions to each chord, we get a series of harmonic functions of corresponding tonalities (Fig. 8.8).

C	C	C	C	C	G	G	G	G	G	G	d*	d	C*	C	C	C
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
T	s	D	T	s	D	T	S	s	D	T	d	T	d	T	S	s
-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	D 18 C
T	D	S	T	D	s	T	d	D	s	T	D	s	s	S	T	T
35	34	33	32	31	30	29	28	27	26	25	24	23	22	21	20	19
C	C	C	C	C	C	C	C	C	C	C	C	c	C	C	C	C

Figure 8.8

From the above symmetry scheme we can note the mirror reflection and antisymmetric arrangement of harmonic functions in the initial and final part (1-11 measure i 35-25 measure). In this case the subdominant function maps into the dominant and vice versa, whereas the tonic function remains invariant. In the middle part (measures 15 - 21) mirror reflection occurs again, but, as opposed to the previous one, it transforms the subdominant function to a tonic one and vice versa, while it preserves the dominant function as unchanged.

The dynamic principle on which this piece is based is reflected in the fact that the parts of the greatest harmonic changes (measures 12 -14 and 22 -24) are mirror-symmetric in respect to the center of the piece. They correspond to the points of the golden section which is accentuated by the appearance of two minor chords (dI in measure 13 and cII in measure 23), in the points of the left and the right golden section (22:35 ~ 0,63...; 3:35 ~ 0,37...).

If each chord is assigned a coefficient of stability we will get the following sequence of stability coefficients and an accompanying diagram of the harmonic flow (Fig. 8.9).

1	2	3	4	5	6	7	8	9	10	11	12*	13	14*	15	16	17
3	2	1	3	2	1	3	3	2	1	3	0	3	0	3	3	2
-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	18 1
3	1	2	3	1	2	3	3	1	3	3	1	1	0	3	3	3
35	34	33	32	31	30	29	28	27	26	25	24	23	22*	21	20	19
C	C	C	C	C	C	C	C	C	C	C	C	c	C	C	C	C

 

Figure 8.9 The stability coefficients of chords and a diagram of the harmonic flow.

In this diagram we can see the intensive changes in the harmonic flow and the points of maximum chord instability near the points of the golden section (measures 12-14 and 22-24). The most unstable diminished chords (3,3,3) occur in measures 12, 14, and 22. The first part of the prelude (measures 1-10) is characterized by a major harmonic crescendo (T-S-D) and the final part (measures 26-35) by a major harmonic decrescendo (S-D-T) which comes to its full affirmation by means of a perfect cadence (measures 33-35).

In looking at this example as an illustration of the possibilities of a symmetry analysis of musical pieces we may conclude that it allows an exact view of regularities, the presence of patterns, and even strong organization principles based on symmetry. By merely listening to a musical piece, one can only glimpse these facts. Thanks to the numerical modeling of all relevant parameters of a musical piece, its symmetries (which have up to now mostly remained out of the scope of musical theory and analysis, or have been marginalized) have now become accessible. In presenting this material, visual materials, such as the diagrams of symmetry abundantly used in this chapter, can play an important role, especially in musical education.

Of course, one or several individual examples cannot provide answers to all the numerous questions about symmetry in music raised in this thesis. This example serves exclusively as an illustration of the application of a complete theoretical system for the formalization of musical language and the symmetry analysis of musical pieces constructed in the preceding chapters. An analysis of a larger sample would provide us with more general conclusions on symmetry as one of the fundamental principles of organization ("good form", according to R. Arnheim) and with a link to the universal principles of the psychology of auditory perception.