Isometric transformations of melodic structure

 

The isometry transformations of a unison melodic structure are made up of the following kinds of transformations:

1. transposition - translation t_x,y for the vector (x,y) mapping each tone (x₁, y₁) into the tone (x₁+x, y₁+y). In particular, for y=0, the transposition (translation t_x) is reduced to translational repetition (Fig. 3.15);

2. retrograde inversion - central reflection O with the center 0(x,y) (Fig. 3.16);

3. retrograde transposition - glide reflection g_y, whose axis is parallel to the y-axis. In particular, if the translation vector equals 0, then the retrograde transposition g_y (glide reflection g_y) is reduced to retrograde repetition m_y (mirror reflection with the axis of reflection which is parallel to the y-axis) (Fig. 3.17);

4. inversion - glide reflection g_x with the axis parallel to the x-axis (Fig. 3.18)

   

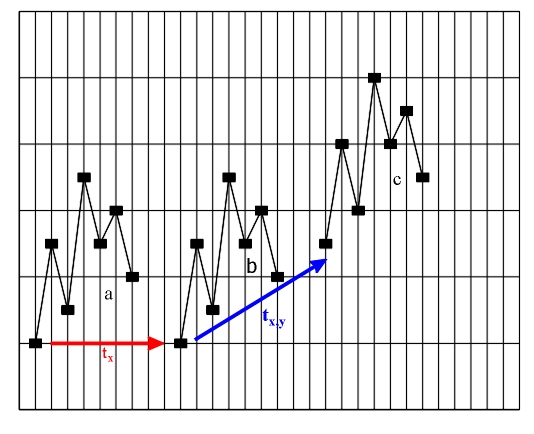
Figure 3.15 a)-b) Translational repetition (translation t_x); b)-c) transposition (translation t_x,y).

 

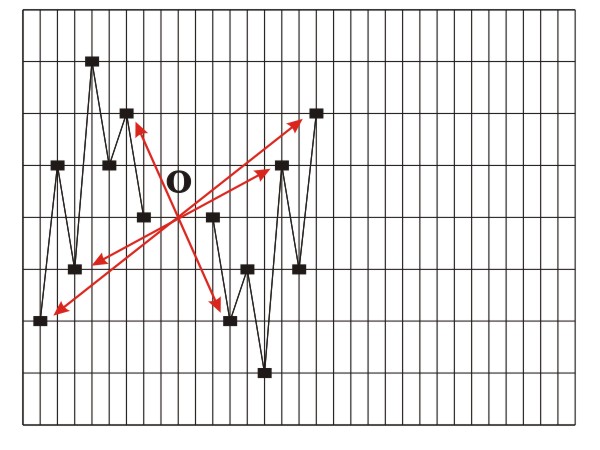
Figure 3.16 Retrograde inversion (central reflection O).

 

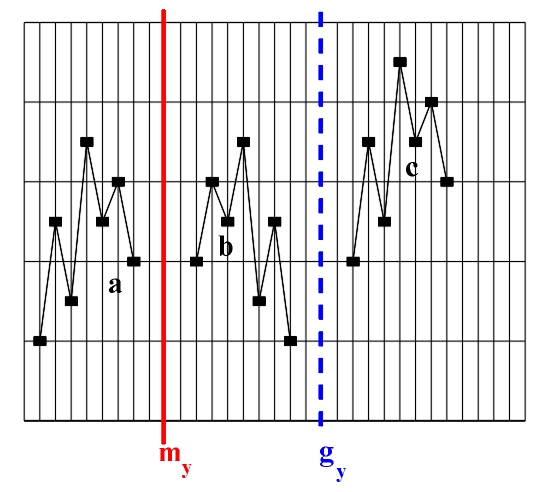
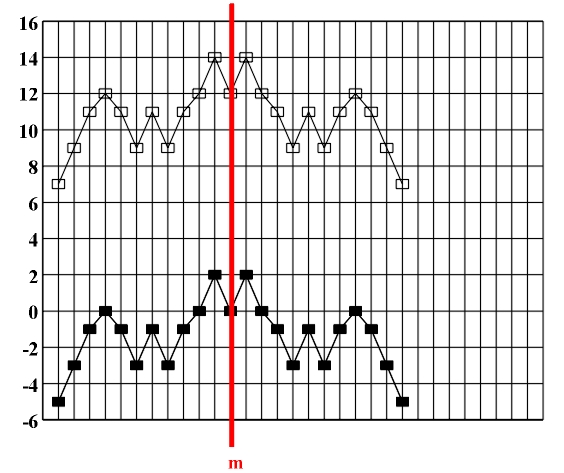
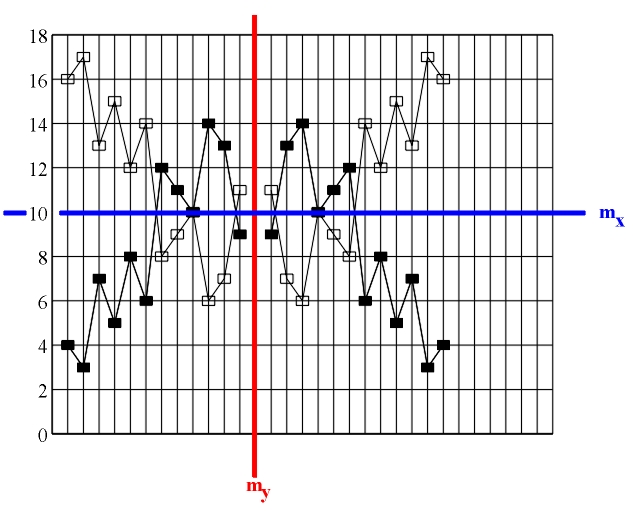
Figure 3.17 a)-b) Retrograde repetition (mirror reflection m_y); b)-c) retrograde transposition (glide reflection g_y).

 

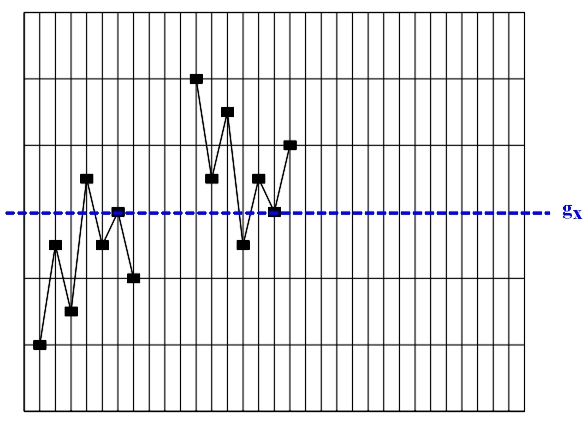
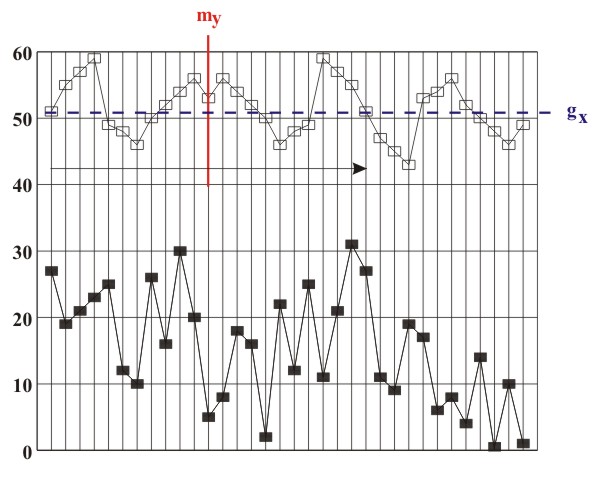
Figure 3.18 Inversion (glide reflection g_x)

Transposition (translation) and retrograde inversion (central reflection) are direct isometric transformations - orientation-preserving transformations. This means that by undergoing transposition and retrograde inversion, ascending intervals are transformed into ascending ones, and descending intervals are transformed into descending ones. Retrograde repetition (mirror reflection m_y), retrograde transposition (glide reflection g_y) and inversion (glide reflection g_x) are all indirect isometric transformations, i.e., transformations that change orientation and transform ascending intervals into descending ones, and descending intervals into ascending ones. The only transformation that does not permit the conjunction of the original with the image, i.e., the congruence of the last point of the original with the first point of the image (for example, the last tone of the theme with the first tone of the variation) is retrograde transposition. Perhaps it is due to this very fact that the term "retrograde transposition", unlike other terms, does not appear in musical theory (see, for example, Skovran and Pericic, 1986).

All of the mentioned isometric transformations are applied to an initial asymmetric figure (an elementary melodic entity, e.g., a motif). Since the result (product) of consecutive application of every two isometric transformations is a new isometric transformation, the existence of two isometric transformations within a melodic structure always results in the appearance of a third isometric transformation - their product, in the studied melodic structure. For this reason we will analyze the products of isometric transformations of a unison melodic structure:

1. the product of two transpositions (translations) is a third transposition (translation);

2. the product of transposition (translation) and retrograde inversion (central reflection) is a new retrograde inversion (central reflection);

3. the product of transposition (translation) and retrograde repetition (mirror reflection m_y) is retrograde transposition (glide reflection g_y). In particular, the product of translational repetition and retrograde repetition (mirror reflection m_y) is a new retrograde repetition (mirror reflection m_y)

4. the product of transposition (translation) and inversion (glide reflection g_x) is a new inversion (glide reflection g_x);

5. the product of transposition (translation) and retrograde transposition (glide reflection g_y) is a new retrograde transposition (glide reflection g_y);

6. the product of two retrograde inversions (central reflections) is transposition (translation);

7. the product of retrograde inversion (central reflection) and retrograde repetition (mirror reflection m_y) is inversion (glide reflection g_x);

8. the product of retrograde inversion (central reflection) and inversion (glide reflection g_x) is retrograde transposition (glide reflection g_y);

9. the product of retrograde inversion (central reflection) and retrograde transposition (glide reflection g_y) is inversion (glide reflection g_x);

10. the product of two retrograde repetitions (mirror reflections m_y) is translational repetition;

11. the product of retrograde repetition (mirror reflection m_y) and inversion (glide reflection m_y) is retrograde inversion (central reflection);

12. the product of retrograde repetition (mirror reflection m_y) and retrograde transposition (glide reflection g_y) is transposition (translation);

13. the product of two retrograde transpositions (glide reflections g_y) is transposition (translation);

14. the product of two inversions (glide reflections g_x) is transposition (translation);

15. the product of inversion (glide reflection g_x) and retrograde transposition (glide reflection g_y) is retrograde inversion (central reflection).

With these compositions of isometric transformations of melodic structure in mind, one notes certain similarities and also crucial differences between two-dimensional geometric symmetry structures - plane ornaments, and melodic symmetry structures. The first difference is in the character of the effect of symmetry transformations: in the case of geometric symmetry structures the effect of transformations is global and results in complete periodicity and regularity of structure, which is not the case with melodic symmetry structures where the action of symmetry transformations is local, i.e., it refers only to individual melodic entities (Fig. 1.5) Another specific property of melodic symmetry structures is the non-equivalence of x and y-axis. As opposed to real infinite geometric symmetry structures (plane patterns) which have two equivalent infinite translations in the direction of the x and y-axes, in the melodic symmetry structures the directions of the x and y-axes are non-equivalent. The finite (modular) y-axis also causes specific limitations as to the position of the symmetry elements. Because of this, within unison melodic symmetry structures, individual elements of symmetry (otherwise present in two-dimensional geometric symmetry structures) do not appear as translations on the y-axis, mirror reflection m_x with the mirror line parallel to the x-axis, etc. For this reason melodic symmetry structures that correspond to unison compositions may only conditionally be called two-dimensional. They are two-dimensional only when the position of each point (tone) is exactly defined by two coordinates (x₁, y₁). However, from the aspect of the equivalency of axes and the choice of the position of the elements of symmetry, they do not fulfill the conditions that a two-dimensional symmetric structure fulfills.

We will show three examples to illustrate the isometric transformations of melodic structure (Figs. 3.19; 3.20; 3.21).

 

Figure 3.19 Retrograde repetition (mirror reflection m) as the basis of melodic structure: B. Bartok, Microcosmos, Vol. 1, Six Unison Melodies, part 6, (Apagyi, 1989).