|
Symmetry as perception factor and the basis of "good form"
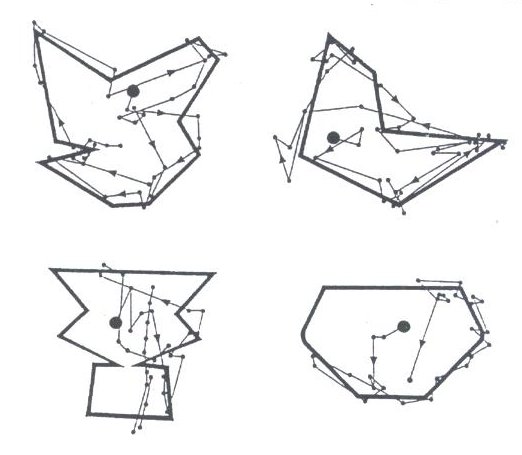
By looking at the history of visual arts and music of the 20th century we can single out two crucial moments with a similar meaning: the appearance of abstract art in painting and atonality in music (Hofman-Jablan, 1988). Up to the present, the unique organizational principle of a painting and music was (mono)centricity - the existence of a center of perspective in visual arts, and a tonal center in music. By breaking away from the principle of centricity all the points of a plane in a picture (and all the tones in a music piece), become equal among themselves. Such a change unavoidably led towards researching other organizational principles and new aesthetics. The aesthetics of visual arts, based on the analysis of the fundamental elements of visual perception, excels in this. The reasons why this type of study always begins in the visual field are twofold. Unlike music which possesses a high level of abstraction and is not directly linked to the representation of reality (for which reason it has suffered less the deviation from centricity), for the visual arts the transition from figurative to abstract art meant violating yet another basic precept: the image as a faithful interpretation of reality. This brought about the transgression of one of the fundamental classic esthetic criteria for the evaluation of a work of art: its level of correspondence to reality. The other reason is that it is much more complicated to study music, a temporal form of art, from the aspect of perception. This particularly relates to the analysis of a symmetric structure of a work of art. In non-temporal arts, such as painting or architecture, the viewer perceives the object as a whole in its static form and can observe the occurrence of equivalent elements simultaneously and in detail, as well as discern the regularity of their arrangement. On the other hand, in temporal arts, such as music, it is an open question: to what extent is the listener capable of registering equivalent elements and particularly of following the symmetry relationships between them, especially if he is dealing with temporally distanced elements linked by more complicated forms of symmetry (e.g., inversion, retrograde inversion…). In this case, as in the plane of visuality, the perception of symmetries will depend directly on the compactness of the image, i.e., the closeness of equivalent elements which allows the joining of equivalent elements into a symmetric subparts. In associating the concept of a "good form" (Arnheim, 1971, 1985) with the definition of symmetry of J. Rosen (1989), we can try to ascertain what makes a symmetric object perceptually more acceptable when compared to an asymmetric object. We can attempt to answer this question by referring to the principle of economy. It is the same principle according to which the movement of light occurs in the shortest path possible, and bees build hexagonal hives with a minimum use of wax. As we study the process of visual perception of a mirror-symmetric object and an asymmetric one, by closely following the eye movements of the observer over the object (Fig. 9.5) we can, in the case of the symmetric object, see that the eye is centered on the axis of symmetry of the object and that it lingers on the points that are almost all on the same side of the axis of symmetry. The other half of the mirror-symmetric figure is perceived almost superficially (Deregowski, 1992). According to the principle of economy, by perceiving one half of a symmetric figure, in reality one perceives the whole symmetric figure. In the case of a more complex symmetric figure, perception is reduced to noting one element, a series of elements equivalent to it and their regular arrangement in the symmetric structure. Thus, from the aspect of the theory of information, a symmetric object carries the maximum information which is obtained by a minimal effort of perception.
Figure 9.5. The eye movement of the observer at the moment of the visual perception of asymmetric and symmetric objects. Discussing organizational principles in architecture and analyzing more complex forms, R. Arnheim says, "There is order on all levels of complexity. The more complex the structure, the greater the need for order... The enemy of complexity is incongruity, that is, disorder. A complex structure joins all elements of varying sizes and shapes, directions, colors and textures, into the same structure and it often builds a whole new form from a variety of more or less dependant parts. Such a divergent structure can easily come apart. A strong basic structure can take a certain amount of deviation without being endangered. This is especially true of accidental deviations, when only "noise" is perceptible, not independent forms. Paul Zucker gave the name "nucleus" to a square representing a set holding steadfastly with the help of a powerful accent such as a monument, a fountain or an obelisk in its center, which joins the "heterogeneous peripheral elements into one visual unit. A powerful structure will impose itself even if it is only partially accomplished." (Arnheim, 1990, p. 159). The comparison of this quote with the process which occurs in music when the tonal center is violated is an interesting one. In one of his lectures A. Webern, one of the co-founders of serialism (besides A. Schoenberg, and A. Berg), stresses the use of non-consecutive, different intervals as one of the most efficient means of disrupting the classical sense of tonality. On the other hand, in his words: "A series is never random nor accidental. It is constructed in accordance with a certain conception. Certain formal aspects must be taken into account, such as steps with as many different intervals as possible, a certain coordination within Reihe, symmetry, analogy and structure construction (e.g. three times four or four times three notes)." In this manner an organizational principle is negated and at the same time substituted for another by coordination, symmetry and note grouping which has its special role, producing in the listener the effect of something familiar, even though the pattern is not repeated mechanically, but rather through a series of different inversions and transpositions of tonal pitches (Fig. 9.6). Formulating the procedure which he consistently accomplishes in all structural levels of a musical piece, A. Webern puts it simply: "We always speak about the same thing, but in a different way." (Fittler, 1992, p. 256).
Figure 9.6. Grouping of notes and local symmetry in A. Webern's Cantata no. 1. (Fittler, 1992). The transition to musical reductionism (minimalism), variation repetition, and the abundant use of symmetry is just one step further. It is the line from G.P. da Palestrina and J.S Bach to S. Reich, P.H. Glass and M. Nyman. Even in the realm of coincidence, in graphic arts based on the principle of chance arrangement (Fig. 9.7) and the stochastic music of I. Xenakis, symmetry substructures may occur as a result of random processes. Already in the moment of deciding to give each number, tone or any other element an equal chance of being used, we are actually establishing an equal treatment among the numbers, i.e., a (random) relationship of equivalence from which the occurrence of symmetry may result.
Many theories of perception accept the gestalt principle on the functioning of the perceptive system according to the law of "pregnancy": the tendency of the perceptive system to identify the most regular, simple and stable structures in each set of stimuli. According to W. Kohler (1938) this principle is based on the logic of neural economy, i.e., the tendency of the perceptive system towards those structures whose perception requires only a minimum of neural effort. Contemporary theories are more apt to accept the validity of the principles of minimum on the functional, rather than in the energetic level. A new challenge in the research of the principle of the minimum comes in the form of the information theory applied on the theory of perception, which explains this principle as a tendency of the perceptive system towards those stimuli that carry the minimal amount of information, thus contributing to relieve the information processing channels. On the other hand the perceptive system also tends towards a maximum specification of the percept. Thus the law of "pregnancy" can also be called the law of optimality (or the minimum-maximum principle). Under the term optimality we understand the inclination towards the most economical processing of the perceptive material (minimum) while retrieving the maximum amount of information (maximum). An interesting physical analogy to the minimum-maximum principle is S. Koffka's (1935) "soap bubble model" - the physical minimum-maximum tendency by which the soap bubble encompasses a maximum amount of volume with a minimum amount of area. The principle of optimality characterizes the behavior of many natural systems. Based on the existing experimental results it can be expected that this principle, as one of the laws of nature, will be applicable on the analysis of the functioning of the perceptive system, as one of the systems of nature. Because perception is treated as an aspect of psychological and physical mapping, it is characterized by an external stimulus domain, rules of mapping and a perceptive co-domain (Markovic, 1993). When identifying the objective characteristics of the stimulus domain which make it perceptively valid, i.e., when determining the properties of "good form" on the visual level, we encounter various aspects of the simplification of art forms which are the criteria of "good form." These are, fore example, a decrease in the number of linear segments and angles of various sizes, a decrease in form dispersion, a decrease in the number of non-connected areas of forms which make up complex structures, a decrease in the distance between linear elements in space... These phenomena are the consequences of the law of perceptive organization based on similarity, proximity, continuity, compactness, etc. All these prerequisites may be treated as part of a unique criterion: the minimization of the number of different classes of equivalence within a stimulus domain. What stems from this conclusion is the direct connection between "good form" and symmetry. Among the most effective visual interpretations of the said prerequisites are optical illusions obtained by their use (Figs. 9.8-9.9). These are abundantly used in Op-art (optical art) and lead one to the suggestion of non-existent objects (subjective Kanizsa contours) (Fig. 9.10), or to the transformation of a series of concentric circles into a spiral (Fraser's spirals) (Fig. 9.11) (Baret, 1970). However, even this effect can be analyzed from the aspect of the theory of symmetry: the circle and the spiral represent the only curved lines in the plane with constant curvature, therefore they belong to the same broader class of equivalence.
Figure 9.8. The devil's fork.
Figure 9.9 Hering's illusion.
Figure 9.10 Subjective Kanizsa contours.
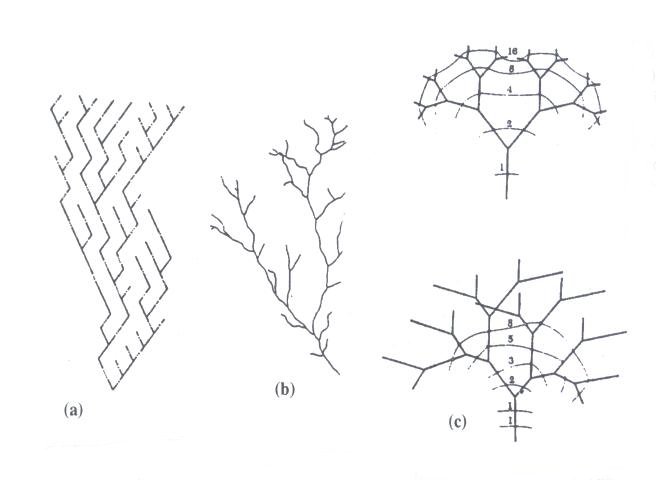
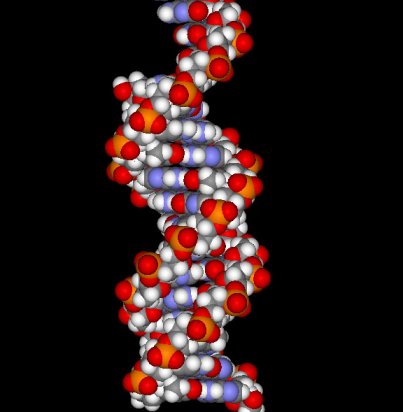
Figure 9.11 Fraser's spiral. Unfortunately, significantly less attention has been devoted to other similar principles and their resulting phenomena in the domain of auditory perception in former experimental and psychological studies. A related example of "subjective tones" induction are the following results: when emitting two or more perfect tones or harmonics of the same basic note, the ear adds the note, as well as several of its harmonic notes. When emitting two random notes a fourth or a fifth apart, the note which is an octave lower (the "tone of difference") is heard. In general, two emitted notes evoke a third which caries out their synthesis - a note symmetric (in regards to frequency) from the higher to the lower, which will play the role of the temporary tonic (Ghyka, 1987, p. 210). This type of phenomena will be analyzed in more detail in the section dealing with antisymmetry and the principle of complementarity. In temporal arts, among the mentioned prerequisites of "good form," an especially important role is played by the principle of continuity which allows extrapolation in time, i.e., the prediction of the further course of the musical piece. It is namely this principle, whose applicability is limited to music of non-aleatoric character, that led E. Surieau to the following conclusion: "For every musical composition a spatial annotation can be conceived, a curve which simultaneously points at the harmony of the piece, its rhythm and melodic line." (Ghyka, 1987, p. 217). Another manifestation of the principle of economy in nature, science and art is the law of modularity - the possibility of constructing a variety of objects from the same initial elements, the principle of standardization and the principle of recombination. We can find examples of modular structures in chemistry, the patterns of modular, self-referential and fractal structures (patterns of growth, the arrangement of tree branches, the "branching" of rivulets in a river delta, etc.), as well in the aspirations of ancient mathematicians towards a universal system of measurement, commensurability, standardization of measurement systems, modular elements in architecture or visual arts (V. Vasarely), the 12-tone music series, etc. All of these forms of modularity, recombination and standardization result in the simplicity of memorizing, construction and reproduction. In conducting studies of this sort, deductions based on analogy can play an important part. An excellent example is P.S. Stevens' Patterns of Nature. Similar consequences may be the results of similar causes (Fig. 9.12). Although it carries a great risk of mechanical linking, the principle of analogy plays an important heuristic role, especially within the theory of models. An interesting example of analogy between symmetry in nature and the symmetry of a musical piece is given by D. Hofstadter who quotes the symmetry of DNA replication and compares it to the symmetry basis of J. S. Bach's Crab Canon (Fig. 9.13). An example of analogy between the arts is seen in the similarity of electronic music scores and abstract painting (Fig. 9.14).
(a)
(b) Figure 9.13 a) The DNA Structure and its scheme; b) J.S. Bach's Crab Canon based on retrograde transposition (Hofstadter, 1980).
Figure 9.14 a) G. Ligeti, Articulation; b) K. Stockhausen, Electronic Study II.
|