|
Antisymmetry, complementarity, bivalence, and ambiguity
In the symmetry analysis of musical pieces antisymmetry is unavoidable wherever opposites occur (consonance - dissonance, major - minor, note duration - rest, etc.). Bivalent symmetry may serve as the basis for studying the contrast between static and dynamic symmetry. The very term "antisymmetry" and the polar dualism of antisymmetric phenomena or properties ("black - white", "yes - no", consonance - dissonance, accentuated - non-accentuated, static symmetry - dynamic symmetry) leads us to the interpretation of antisymmetry as a symmetry of opposites. Sin embargo, all opposites can at the same time be considered also as complements. Thus, we do not speak of "opposite colors" in painting (red - green) but about complementary colors. In the set theory, an empty set is a complement of the universal set and vice versa. The treatment of antisymmetry as complementarity presents a very large area of researching the psychological and esthetic significance of the principle of complementarity. The rule "opposites complement one another" reminds us of the rise of impressionism and of revolutionary changes in 20th century painting brought about, among others, by the influence of Delacroix's research and Chevreul's law of complementary colors (Itten, 1973). It also reminds us of H. Moore's sculptures in which the material part of the sculptures and their complements - the empty spaces are treated quite equally (Fig. 9.18), of the black-and-white ornaments which introduce the equivalence of the figure and the ground (Fig. 9.17), of the rest in music, poetry and speech and of its psychological effect, etc. The following verses from Tao Te Ching illustrate the value of "negative space":
but it is the center hole that makes the wagon move. We shape clay into a pot, but it is the emptiness inside that holds whatever we want. We hammer wood for a house, but it is the inner space that makes it livable. We work with being, but non-being is what we use 1".
Figure 9.18 H. Moore, Reclining Mother and Child. Figure 9.19 After-images. As we observe the relationship between "static" and "dynamic" not only as a relationship of opposites, but also as one of complements, it is made more clear that the same element may have a two-fold function. Thus the golden section, the dynamic bearer of symmetry in nature and art possesses a universal esthetic function. At the same time it represents a proportion which determines the enthasis of a column in architecture - its "dynamic center of energy," the proportion which corresponds to the culmination points within many music pieces, the proportion present by means of Fibonacci's sequence in Le Corbusier's Modulor (Fig. 9.20) and in the spirals of growth of living organisms (Fig. 7.19). At the same time it occurs in the proportions of static structures: regular polyhedra of maximum symmetry, icosahedra and dodecahedra (Fig. 7.17).
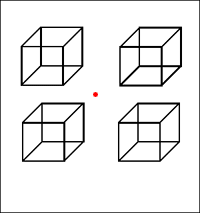
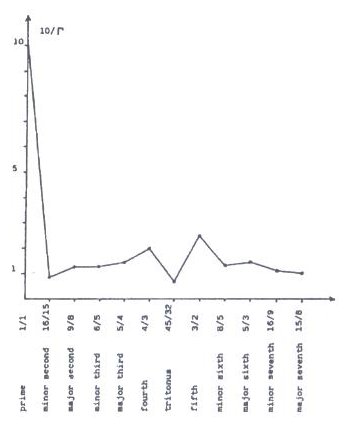
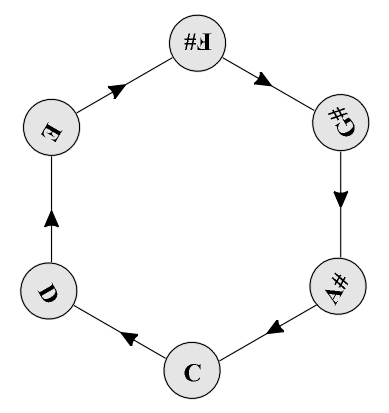
Figure 9.20 Le Corbusier, Modulor. Colored (polyvalent, permutational) symmetry which occurs in visual arts beginning with the ornamental art of ancient civilizations, can play a part in the symmetry analysis of all polyvalent musical elements. The occurrence of different aspects of polyvalence in contemporary art and science - polyvalent logic, cubism (polycentrism in painting - the attempt to present an object observed simultaneously from several points of view), and abundant applications of polyrhythmic and polymetric in music is almost simultaneous and chronologically coincides with the beginning of the twentieth century. Bivalence, antisymmetry, the balance of opposites and the law of complementarity are all connected to the subject of ambiguity: the possibility to perceive one object in two different ways at the same time. Unlike antisymmetry, where the opposites are clearly visible, in the case of ambiguity our perceptive system vacillates between two possible interpretations and, being indecisive, is thrown off-balance. Thus, the golden section expresses clarity and contrast, not internal contradiction which occurs when a line segment is divided into two approximately equal parts, when our visual perception vacillates between mirror symmetry and asymmetry. Typical examples of ambivalence are optical illusions which occur when the viewer is uncertain as to what is the figure and what is the background, i.e., when both the figure and the background convey two different but equally meaningful pieces of information. In the visual plane an example of this phenomenon is the Necker cube (Fig. 9.21) or the Koffka cube (Fig. 9.22) based on the ambiguity of the relationship "front - back" or "convex - concave". In music such perceptive dilemmas are elicited by the tritone ("diabolus in musica" - extreme dissonance), the only interval identical to its complement (Fig. 9.23), or the use of the hemiola effect (organizing sequences of six notes of equal durations into groups 3×2 or 2×3, used in the works of J.S. Bach and F. Chopin). We come across interesting examples of the visual effects of ambiguity in the works of Op-art authors where as a result of the incessant vacillation between the figure and ground the picture seems to scintillate (Fig. 9.24). Such optical illusions may also be grounded in an undefined "convex - concave" relationship (Fig. 9.25) (Gombrich, 1979). A similar situation occurs during the transition of one element from a whole structure (e.g., space, or tonality) into another in such a way that at one moment it simultaneously belongs to both structures. M.C. Escher's reptiles depart from the plane of the drawing, wander through three-dimensional space and return to the drawing (Fig. 9.26) in a manner similar to the flow of the cycle of modulations in Bach's Endlessly Rising Canon (Fig. 9.27). Rising over the regular tonality sequence, the canon returns to its initial tonality, only this time an octave higher, building thus an infinite dynamic structure - helix, similar to the one built by the "aperiodic crystal"- DNA molecule (Hofstadter, 1980).
Figure 9.21 Rubin's "vase - face" illusion.
(a)
(b) Figure 9.22 Necker cube (a) and Koffka cube (b) Figure 9.23 A curve showing the classification of intervals depending on the auditory sensation they produce (according to L. Euler).
Figure 9.24 R. Neal, Square of Three.
Figure 9.25 J. Albers, To Monte Alban.
Figure 9.25 M.C. Escher, Reptiles.
Figure 9.27 J.S. Bach, Endlessly Rising Canon, a cyclic hexagonal scheme of modulations (Hofstadter, 1980). 1Translation by Stephen Mitchell, 1988
|