|
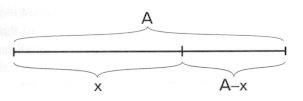
In analysing the dimensions of the work, we must draw a distinction between proportions of a dynamic nature, and those which are static. For while those of a dynamic nature - like the "golden section" discussed below, and the systematic diminution of dimensions - are always connected to a directional tension of some kind, positive or negative, those static in nature - below under this are listed symmetry and geometrical bisection - are characterized by a harmonious balance of forces. The golden section is a formal element in the construction of this Sonata at least as important as was the periodization of 8+8 or 4+4 bars in the Viennese classical style. In essence, the golden section (sectio aurea) is a simple pair of proportions: a length divided into two such that the proportion of the whole to the larger section matches that of the larger to the smaller section. 6) If the whole length is marked "A" and the unknown larger section "X", then the value of the smaller section will be "A - X":
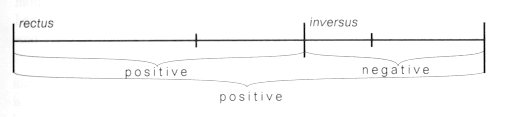
On this basis, therefore, the equation of the golden section is: A : X = X : (A - X) Since the result of this equation is that "X = 0.618A", then we see the following formula: A : 0.618A = 0.618A : (A - 0.618A) or A : 0.618A = 0.618A : 0.382A In practice, the consequences of this for analysis are that 1. the larger section of any length divided according to the golden section is equal to the length of the whole ("A") multiplied by the proportional factor of 0.618 (i.e. X = 0.618A); 2. the value of the smaller section is found by multiplying the length by 0.382 (i.e. 0.382A). As an experiment, let us find the golden section of movement I. Its overall length is 443 bars, therefore the longer section (based on the equation X = 0.618A) will be 0.618 x 443 = 273 bars. Thus formally and tonally the golden section coincides with the focal point of the movement, the statement of the first subject in the recapitulation (b. 274). The golden sections tabulated below entirely fulfil the strictest geometrical requirements. It is an easy matter to check the data with a slide-rule. 7) The descriptions "positive" and "negative", used to distinguish between the two possible intersections, refer to the order of the sections: positive = long + short and negative = short + long.
The unit of form in which the golden section appears, acquires a tension character with a plus or minus sign. The easiest way to imagine this is to regard symmetry as a condition of balance (tension-wise neutral), since its focal point is in the centre:
whereas the focal point of the golden section in comparison to this has shifted in a direction either positive or negative:
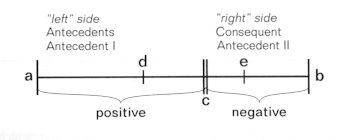
An analysis of the Sonata reveals that a positive intersection is accompanied by a tensing of the formal muscles, in essence an elevation or an increased density of material, while a negative intersection is accompanied by a waning of the dynamic forces, a subsiding. The golden section is only found together with certain types of themes, namely the "creeper" type, motor-dynamic and polyphonically treated types, these by their very nature not mingling easily with 8+8 i.e. 16 bar symmetry. So much so, that the 8 bar melodies appearing in movement III in bs. 144-159 and 379-394 have involuntarily acquired the name "strophes", because they stand out completely from their asymmetrical surroundings. The development section of movement III will later allow us to examine more closely the static-dynamic question. As a general rule the "left" and "right" sides of binary forms, as well as the antecedent (Stollen) and consequent (Abgesang) of anapaest form 8), including the antecedents I and II that this contains, bring into conjunction sections with positive and negative intersection:
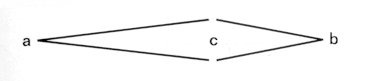
As a result, the two dynamic figures (complementing one another like a reflection) combine to make a round static unit. The intersections "d" and "e", drawn into the field of attraction of the central point "c" (see above diagram), mark the unbroken arching of the form's tension curve:
In the majority of cases, the node point "c" is itself the golden section of the length "a - b" (a good example occurs immediately in the 17 bars that begin movement I). Evidence that Bartók was preoccupied early on with the problems of the golden section is provided by the clattering F# minor of the Allegro barbaro, which results in units of 3 - 5 - 8 - 13 bars, exactly the most characteristic and pure proportions of the golden section. The proportions listed are accompanied by only a few marginal notes, as the golden sections and their combinations follow with almost seismographic accuracy the carefully articulated formal and tonal thought - indeed, they prove to be absolutely identical with it. If we are therefore aware of the formal and tonal position of the units due to be analysed, of their function in the construction of the work; in a word, their dependency, or derivation, their relationship to neighbouring and related sections, their role of attraction or repulsion - then this naturally provides an explanation of the inner structure and the golden sections of the unit analysed as well. Let us see an
example. In movement I bs. 2 - 18, the handling of the leading motive 9)
can be considered a unit, equally from the thematic, dynamic and formal
standpoints. In brief it divides up as follows:
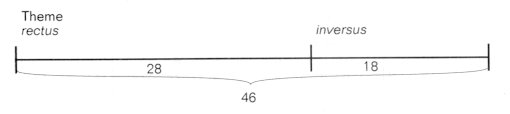
The most practical way of counting will be to take triplet units (3/8), in which case the whole section consists of 46 units, the golden section being 28 (because 46 x 0.618 = 28). This result matches our expectations, as the rectus sections contain exactly this number of units:
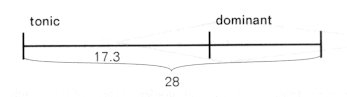
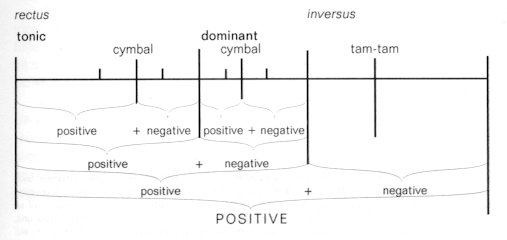
Now let us extract from this set of relationships the rectus section, which takes up the first 28 units. Geometrically the positive intersection should fall in the first third of the 18th unit (because 28 x 0.618 = 17.3), and in fact this position coincides exactly with the second appearance of the theme in the dominant:
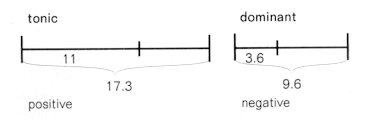
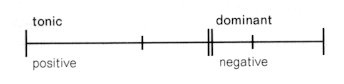
Now let us consider individually the tonic and dominant sections of the theme. Both units are clearly divided in sections by the cymbal stroke, furthermore the tonic section is split in a positive direction, the dominant in a negative one:
(because 17.3 x 0.618 = 11, and 9.6 x 0.382 = 3.6). The positive and negative intersections are here so intertwined with each other, they arch like the rising and falling of waves:
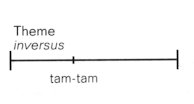
The crests of the waves link to form a positive intersection (the double line in the diagram). The contrary image of this positive intersection is delineated by the "inversus section", i.e. where the entry of the tam-tam gives it a negative (minus) sign:
Following from this, the rectus and inversus sections (positive and negative intersections) complement each other mirror-wise, while as an overall form they combine in a positive intersection, signifying that the general progression is an upward moving one:
Measurements carried out on even the smallest formal units prove to be equally persuasive. Let us take as an example the dominant section: in the part extending as far as the cymbal stroke, the long eb note of the motif falls at the positive intersection, and in the part following the cymbal the side drum entry falls (symmetrically) at the negative intersection:
Likewise, the positive intersection of the part of the tonic section extending as far as the cymbal, falls at the third entry on c# on the timpani, and the symmetrically falling negative intersection of the part following the cymbal is at the side drum stroke. From these positive and negative intersections linked in pairs arises a continous fluctuation on a large and a small scale, one whose various undulations eventually meet with a positive (plus) sign, hence producing a powerful dynamic elevation:
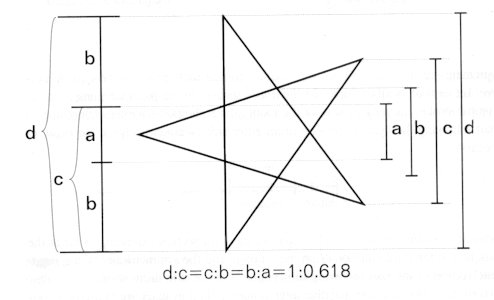
It is characteristic of this complex, "potential" form, that the golden section always lies at the most important point in the divided formal unit, and that the longitudinal wave-formation caused by the intensification and relaxation in the occurrence of intersections ("nodes") can be fully felt. The golden section is the framework within which beauty and life touch one another at the deepest level. The golden section is a symbol of life, a formula taken from nature as it were, contrary to everything we know to be disorganized, distorted, and lifeless. One of the most beautiful of its symbolisations is the pentagram, every proportion of which without exception conforms to the golden section: 10)
6) Or the larger section is the geometrical mean of the overall length and the smaller section. 7) A question the reader may justifiably ask is why the golden section is measured by bar numbers (or note values) and not to time. In the author's opinion, the metrical beat is music's heart beat, and as such, ranks higher than the measurement of time. 8) See further text regarding the connection between anapaest form and Barform (translator). 9) The 1st bar, as it were, opens an endless perspective onto "timelessness"; the organic life of the work has been counted as beginning only from the 2nd bar. 10) Some data regarding the practice of the golden section: in its most beautiful form, the golden section finds expression in Gothic architecture. The Lancer of Polykleitos, as has been demonstrated, is in every proportion constructed to golden sections. Fibonacci, when studying the fertility of rabbits, came into possession of an arithmetical progression, every unit of which stood in a golden section relationship with its neighbouring unit, each number being at the same time equal to the sum of the two preceding numbers: 2, 3, 5, 8, 13, 21, 34 etc. The spirals going in one direction or another on the stalks of flowers also follow the numerical proportions of the above progression. In the opinion of Sainte Lague, the golden section is the characteristic of living forms, while it is lacking in crystalline and inorganic forms, precisely in connection with their pentagonal qualities (the calculation 0.618 involves the root 5); think of the large role played by pentagonal radii in the organisms of plants and primitive organisms.
|