 |
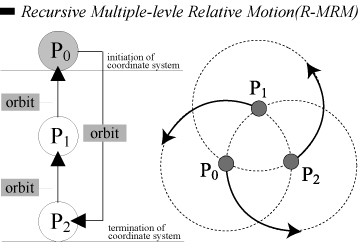 |
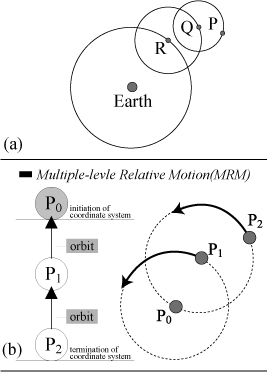
Recursion is the concept of the well-defined self-reference, and a way of specifying a process by means of itself. In LOGO [8-10], a number of procedures have been executed with recursive method to draw a series of geometric patterns. A recursive procedure is a procedure that uses itself as one of its parts. In the relative motions as the solar system, we can assume the Sun serves as the initiation of an absolute coordinate system, which does not move, and the Earth serves as the termination of a coordinate system, which orbits the Sun. Compared with relative motions, recursion is a operating mechanism that initial coordinate system orbits the termination, and the termination also re-influences the initiation. Consequently, mechanism of recursive relative motions is a self-circle hierarchical structure (Fig. 4), and nevertheless relative motion is a top-down model (Fig. 3b).
|
|
The significant influenced factors with recursion on generated patterns include: (1) the number of recursive levels of relative motions, (2) the radii of coordinate system, and (3) the angular increments for orbital velocity of motions. Evidently the number of recursive levels straight influence on patterns formation, and complicate the operating mechanisms of relative motions. To manipulate the radius of coordinate system is to influence the scales of patterns generated. While more degree of radius measurements are manipulated, and then it is difficult to constraint the scopes of geometric plane generated and eventually capture the patterns. In order to illustrate the effects of recursive method on pattern formation of relative motion, we will use the following manipulations of angular increments: (1) ratios of angular variances, and (2) balance of total clockwise and counterclockwise angular amounts. Furthermore, we force to make the radius of each coordinate system equal 1 pixel, and implement the angular differences to generate patterns.
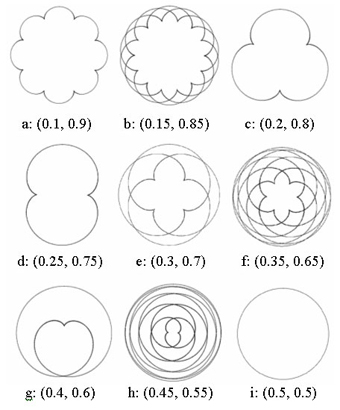
To manipulate ratios of angular variances means that implement the different ratios in the relationships of angular increments for orbital velocity of each coordinate system between the relative motions. Fig. 5 shows the variations of generated patterns with manipulating the different ratios of angular increments using two recursive levels (simplify as 2-RL). To control the conditions for balance of total clockwise and counterclockwise angular amounts is to manipulate the diversity of situations for growth and decline in whole relative motions. Fig. 6 illustrates the diversity of patterns generated with manipulating the different balances between total clockwise (P0 -> P1 , P1 -> P2 ) and counterclockwise (P2 -> P0 ) angular amounts. The maximum of total counterclockwise angular amount is -24, and minimum is -0.1.
 |
 |
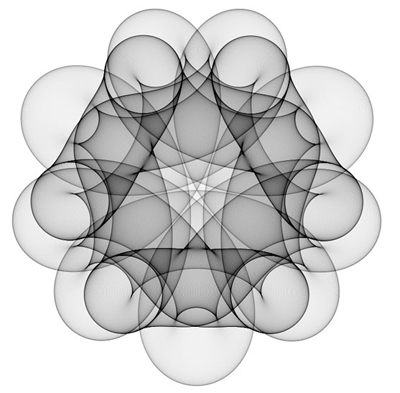
Angular increment with slight variations will result in the slightly movement variations of trajectory, and progressively generate new trajectories toward inner patterns. Fig. 7 demonstrates the 4-RL and 5-RL visualized pattern that based on the frequencies of movement visited for manipulations of slight variations.
 |
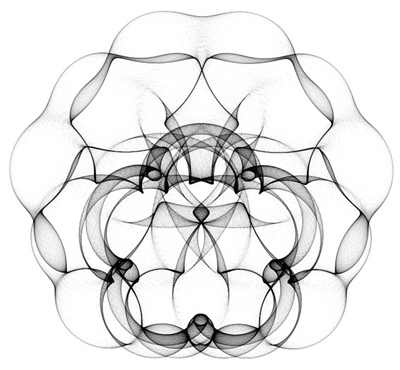 |
4-RL: 24,000,000 iterations |
5-RL: 5,400,000 iterations |
The term pursuit curve in many mathematical books simply considers a chaser in pursuit of a target [11-13]. It is also called pursuit problem what means an object or target moves along a given curve and a second object or pursuer follows or pursues the target. The object moves in the direction of the target at all times. The simple mathematical concept of a pursuit curve can serve as the starting point for creating wonderfully intricate geometric patterns. Sharp (1999) had conducted to an experiment of pursuit curves, and supposed that four bugs were at the corners of a square. They started to crawl clockwise at a constant rate, and each moving toward its neighbor. Superimposed snapshots of the bugs' progress represented an intriguing pattern [14].
The significant influencing factors with pursuit on generated patterns include: (1) what kind of movements for coordinate system of the pursuit target, (2) the pursuit velocity of the chaser, and (3) how manipulate the rules that pursue the alternative targets. The pursuit velocity immediately influences the pursuit trajectories. When if the pursuit velocity is greater than the ones of target, and therefore the pursuit trajectory resemble in the results of movements of the pursuit target.
In the Solar System, we can set the space ship to pursue the alternative targets according as rules manipulated. For instances of Fig. 8, we manipulate Earth-Sun and Moon-Earth-Sun relative motions, and space ship proceed from the Sun to pursue repeatedly the decided one of alternative targets. Obviously different pursuit velocity causes the apparent differences in movements of space ship.
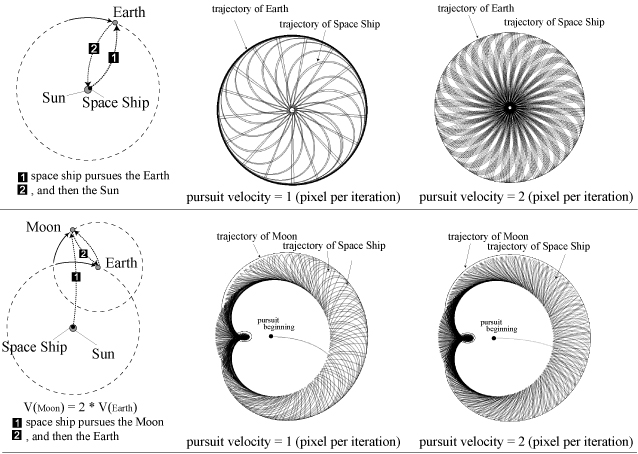 |
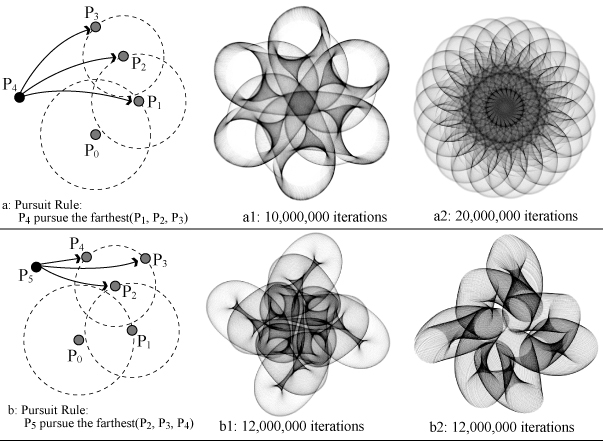
The trajectories of pursuit motions can be highly complicated. When the systems of multi-level relative motions increased, the trajectories became unpredictable and sometimes peculiar. In order to generate the more complicated trajectories, we can arbitrary manipulate the different pursuit rules, which is always pursue the farthest coordinate system. The movement of which one of alternative pursuit targets affects the appearances of pursuit trajectories based on the distances between chaser and each of pursuit targets. Fig. 9 demonstrates the differences in patterns created with the diversity of coordinate systems of relative motions. The pursuit velocity of both in Fig. 9 equals 1 pixel per iteration. The both of Tab. 1 and Tab. 2 show as the detailed parameters of Fig. 9.
Tab. 1: Detailed parameters in Fig. 9a
|
Tab. 2: Detailed parameters in Fig. 9b
|
 |
Contents: [Index] |
|||
Recursion and Pursuit |
|||