 |
 |
Relative motion everywhere performs in our life and the Solar System, and it can be interpreted that a moving object can only have one velocity at any moment when observed by single observer. Humankind has always been fascinated by the night sky, and, in particular, by the movements of the Sun, the Moon, and the objects which the ancient Greeks called plantai ("wanderers"), and which we call planets . Moreover, the planets were vital to Astronomy. Eudoxas (408-355 BC), a Greek mathematician [1], who was the first to describe a theoretical explanation of the movements of the planets, and proposed model became known as the Geocentric model of the Solar System. Each planet is attached to differing spheres, which revolve around the Earth as its center. From philosophical viewpoints, orbital pattern is circular in this model, and because of it is the most perfect imaginable shape. For an alternative model, Aristarchus (310-230 BC), a Greek astronomer [2], who was the first to propose the Heliocentric model, that the Earth and other planets orbited the Sun.
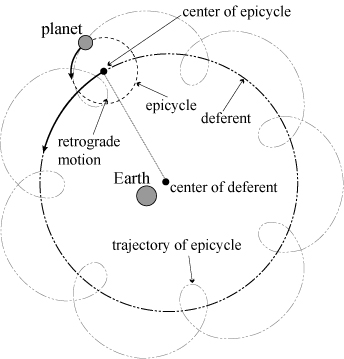
Refinements of Geocentric model for capable of accurate predictions, Claudius Ptolemy (85-165 AD), a Alexandrian philosopher, who proposed in his famous book, now known as the Almagest [3], remained the dominant scientific picture of the Solar System for over a millennium. In significant modifications of Ptolemy, the deferent is a large circle centered on the Earth, and the epicycle is a small circle whose centers move around the circumference of the deferent [4]. Fig. 1 shows the modifications of Ptolemy for Geocentric model of the Solar System. Occasionally, planetary motion sometimes seems in the opposite direction to its apparent direction of rotation around the Earth, and performs the phenomenon of retrograde motion [5]. This confusing behavior became the riddle of the astronomers, embarrassing the Greeks, who believed in order and regularity. Obviously, the trajectory of deferent represents a circle. Nevertheless, based on occasional bouts of the retrograde motion, the trajectory of epicycle has a certain appearance of a petal.
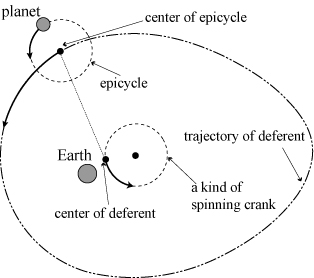
In John's book [6], he trickily refined the Ptolemaic system. John modified the center of deferent to serve as a kind of spinning crank, which was called a moveable eccentric, and produced an egg-shaped deferent as the Mercury's apparent trajectory in the heavens (see Fig. 2). John proposed that no modern theory exists to explain the miracle of conscious life or the cosmic coincidences that surround our planet. John also revealed the exquisite orbital patterns of the planets and the mathematical relationships that govern them in his book. For instances, with the Sun back in the center, he represent the orbits of Venus and the Earth and draw a line between the two planets positions every couple of days. Because Venus orbits faster the Earth, and so these lines represent the beautiful geometric patterns.
|
|
Hipparchus (162-126 BC), a Greek astronomer [7], who created detailed studies of the motions of the Moon and the Sun, and he found some heavenly bodies necessary to employ three or four circles that moved around each other. Within the illustrations of Fig. 3a, a planet P thus moves in a circle around the mathematical point Q, while Q moves in a circle around the point R, and R moves around the Earth, every point or object moving at its own velocity and appropriate choices of radii for the circles. Relative motion can prove consequently the mechanism for the orbital motions with moving around each other of the heavenly bodies. The number of heavenly bodies moved around with relative motion can be unlimited in theory, and nevertheless the operating mechanism of relative motion can be surely simplified as the illustrations of Fig. 3b. P0 is the initiation of the absolute coordinate system for relative motions. P1 represents the point moving on plane P0 and also the origin of plane P2 . P2 is the termination of coordinate system, and represents the point moving on plane P10 . P1 and P2 simultaneously move at the counterclockwise relative to each its superior coordinate system.
Contents: [Index] |
|||
Introduction |
|||