| >
LUNDA DESIGNS If we enumerate small squares through which the singular mirror curve passes by 1,2,3,... until the closed curve is complete, and then reduce all the numbers modulo 2 (replacing every number by its reminder, when dividing it by 2), the result will be a 0-1 (or "black"-"white") mosaic: a Lunda design Lunda designs possess the local equilibrium property: the sum of the integers in every two border unit squares with the joint reference point is the same, and the sum of the integers in the four unit squares between two arbitrary neighboring grid points is always twice the preceding sum. From this, results the global equilibrium property: the sum in each row is equal, and the same holds for the columns. The local, and the global equilibrium property resulting from it, holds as well if we enumerate a curve and reduce all numbers modulo 4. In particular, by enumerating a regular curve (with the mirrors incident to grid edges) and reducing all numbers modulo 4, we obtain four-colored Lunda designs, where every reference point is orderly surrounded by numbers 0,1,2,3 and the disposition of that sequences around the points is alternately clockwise and anti-clockwise. The correspondence between monolinear mirror-curves and Lunda-designs is many-to-one, so a same Lunda-design can originate from several classes, consisting of different mirror-curves. Try to find such classes of mirror-curves. 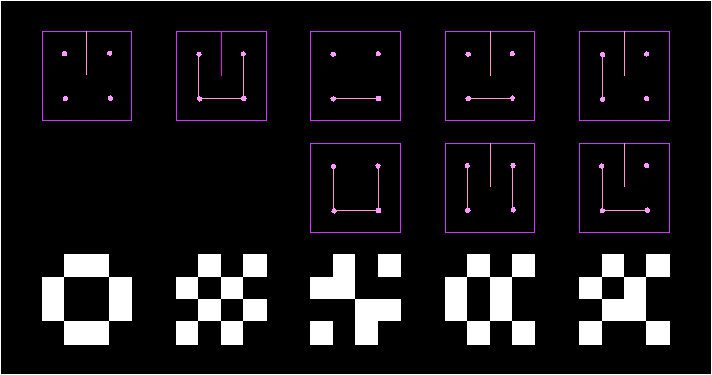 |