A plane topological disk (i.e. a plane region without "holes"), consisting of n edge-to-edge adjacent squares is called a polyomino. Instead
of squares we could use n equilateral triangles or n regular hexagons, and to obtain, respectively, polyiamonds or polyhexes. We will restrict our discussion to polyominoes (with polyiamonds and polyhexes the situation is absolutely the same). For every polyomino we could distinguish it's shape and orientation ("left" and "right" form). For polyominoes not having a reflective symmetry, we may
distinguish (or not) their "left" and "right" form. According to this we have two possible equality criteria: Till now, there is no formula for calculating the number of different polyominoes, but only some results (for smaller values of n), obtained by empirical derivation.
In every border square cell of a polyomino we could introduce
two-sided mirrors perpendicular to the internal edges in their
mid-points. After a series of reflections,
the ray of light will "describe" the shape: a closed Dragon curve.
If we denote a reflection in a border mirror by 0, and a reflection
in an internal mirror by 1, we have 0-1 words
(or symbols) for polyominoes, where these words
are cyclicaly-equivalent (this means, could be
readed starting from any sign 0 or 1 and ending in it):
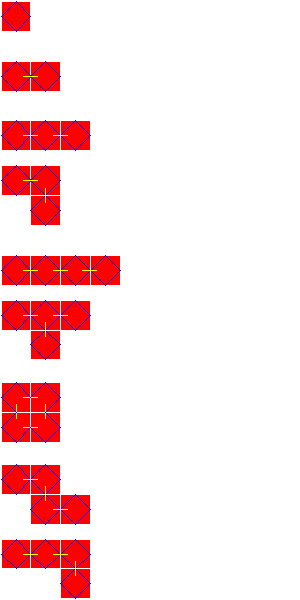 0000 for polyomino 1.1
0000 for polyomino 1.1
From their symbols we could directly make conclusions about the symmetry: every reversible word denotes polyominoes with a sense-reversing symmetry (they don't have "left" and "right" form); irreversible symbols correspond to the polyominos appearing in the "left" and "right" form (e.g. 4.4 and 4.5). That symbols (or binary numbers) we could translate into hexidecimal numbers and to every polyomino asign exactly one such number. For example, this could be the minimum of all such cyclic-equivalent symbols (e.g. to the polyomino 2.1 correspond cyclicaly-equivalent symbols 00010001, 00100010, 01000100, 10001000 and the minimum of them is 00010001 = 11 in hexidecimal system. Hence, we have the notation for polyominoes where to every polyomino corresponds exactly one such number, and vice versa. (Opened question: find the general algebraic form of number determinimg a polyomino? Namely, some numbers will determine "opened polyominoes", "holow polyominoes" or "overlaping polyominoes", that are not included in our definition, and other will determine "real" polyominoes.) POLYOMINO GROWINGEvery (n+1)-omino we derive from some n-omino by adding to it a single square. Certainly, the addition operation is a positional one, that is, the result depends from the position where we add the new square. Here we have the following addition rules:
This "algebra" could be successfuly used for the computer enumeration of polyominoes. In each step we need to derive (n+1)-minoes from n-minoes by adding a square, to test the equality of the (large number) of polyominoes obtained and to make a complete list of the different (n+1)-minoes obtained. The main problem in such a derivetion will make "undesired" edge contacts (e.g., in parallel edges, producing "hollow" polyominoes).
LUNDA POLYOMINOES Polyominoes (either black or white) appearing in Lunda designs will be called Lunda polyominoes. The possible shape of Lunda polyominoes is conditioned by the local equilibrium condition for Lunda designs. Therefore, some polyominoes are inadmissible (e.g. 4.3, or the following 10-minoes) as Lunda polyominoes. On the other hand, in Lunda polyominoes are included also "holow" polyominoes. By introducing the concept of Lunda animals, P.Gerdes in his book "Lunda geometry: Designs, Polyominoes, Patterns, Symmetries" obtained the first approximation for the total number of different Lunda n-ominoes. |