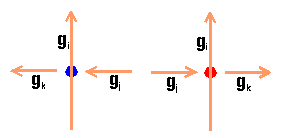
DIAGRAMS The other point of view to the classification of such perfect curves is that of knot theory. As mentioned before, every such curve can be simply transformed into an interlacing knotwork design, this means, into a projection of some alternating knot. In the history of ornamental art, such curves occur most frequently as knotworks, then as plane curves. Even the name Brahma-mudi (Brahma's knot) denoting such Tamil curves refers us to the knots. In order to classify them, we will first transform every such knot projection into a reduced (proper) knot projection - knot projection without loops, by deleting cells with loops.  This way, we obtain reduced knot projections with the minimal number of crossings. Two such projections or knot diagrams are equal if they are isotopic in the projection plane as graphs, where the isotopy is required to respect overcrossing respectively undercrossing. In order to classify our curves, treated as knot projections, we will define an invariant of knot (or link) projections. Let a reduced oriented knot diagram D with generators g1, ..., gn be given. If the generators gi, gj, gk are related as in the left figure, then aii=t, aij=1, aik=-1; if they are related as in the right figure, then aii=-t, aij=1, aik=-1; in all the other cases aij=0. The determinant d(t)=|aij| is the polynomial invariant of D.
For example, for the oriented diagram of the knot 52, d(t)=t5-t3-5t. The writhe of D, denoted by w(D), is the sum of signs of all the crossing points in D, where the sign is +1 if the crossing point is "left", and -1 if it is "right". It is the visible property of every knot projection: |w(D)| is the type of the knot projection. There are some important properties of the integer polynomial invariant d(t)=cntn+... +c1t: According to the last three properties, in the set of all polynomials d(t) we may distinguish even functions (d(t)=d(-t)), containing only even degrees of t, corresponding to amphichiral knot projections, and odd functions (d(t)=-d(-t)), containing only odd degrees of t, which are invariant to a change of orientation of the knot projection. For example, to the knot 31 correspond odd projection polynomial t3+3t, and to the amphichiral knot 41 the even polynomial t4-2t2. Let us also notice that this polynomial projection invariant makes a distinction not only between non-isomorphic knot projections of prime knots (e.g. two projections of the knot 75, to which correspond, respectively, the polynomials t7+3t5-4t3-7t and t7+2t5+t4-4t3-7t, but also between non-isomorphic knot projections of composite knots (e.g. three non-isomorphic projections of 41#31, with their projection polynomials t7+t5-2t3+5t2-3t, t7+t4-3t3-2t2+3t, t7+t5+2t4-2t3+t2-3t, respectively).   Rectangular square grid RG[2,2] is the minimal RG from which we could derive some nontrivial alternating knot (different from unknot) - the knot 31. From RG[3,2] we could obtain 74, 62, 31+#31+, 51, 52, 41 and 31, where different mirror-arrangements will give the same projection. 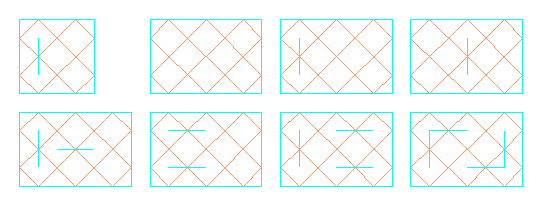 Can we derive every knot projection from some RG? Which knot projections could be obtained from a particular RG? Which mirror-arrangements in some RG result in the same knot projection? Find the minimal RG for a given knot! Can we obtain non-isomorphic projections of some knot from a same RG? These and many other problems connected with mirror-curves represent an open field for research. |