|
LEONARDO
The construction of knot designs, closely connected with mirror curves, occupied the attention of two of the greatest
painters-mathematicians: Leonardo and Dürer. In some of their constructions, they very efficiently used the
following geometrical property: for a rectangular square grid RG[a,b]
with the sides a and b, if a, b are relatively prime the result is always a single closed curve covering uniformly the square tiling of a rectangle.
 
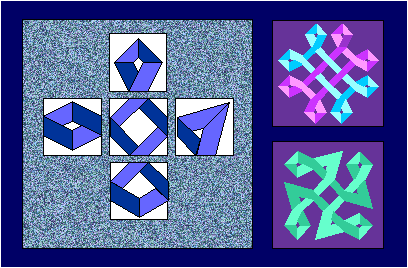
Let us notice one more beautiful
geometrical property: such curves can be obtained by using only few different
prototiles. For the construction of all the curves, with internal mirrors
incident to the cell-edges, three prototiles are sufficient in the
case of a regular triangular tiling, five in the case of square, and 11
in the case of hexagonal regular tiling.
Using their combinations occurring
in the 11 uniform Archimedean tilings, or the prototiles producing the
impression of space structures and colored prototiles, we may obtain very
artistic interlacing patterns belonging to the so called modular design:
the use of few initial elements ("modules" - prototiles) for creating an
infinite collection of designs.
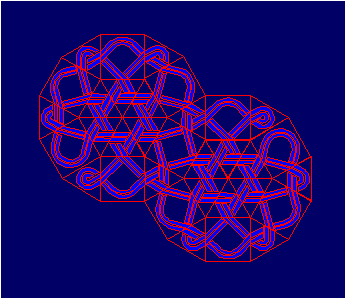
The curves obtained from Archimedean
tilings remind us of the optical phenomenon: change of the direction of
a light ray transferring from one physical environment to the other.
|