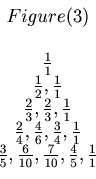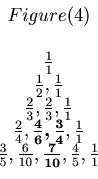


: The mathematical background for
: pascal like triangles
: Abstract
Contents
First we are going to study the theory of Russian roulette. Some people may think that Russian roulette is not a good topic to study, so the authors are going to use another game later in this article instead of the Russian roulette, but the authors want to show how high school students could discover new facts, so they are going present the original problem students studied in the class room.
One of the authors (Miyadera) who is a high school teacher taught the Russian roulette game in his class. The problem is presented in Example 1.
Example 1: Suppose that two persons are going to play the Russian roulette and the gun has 6-chambers and initially 2-bullets in them. When a player receives the gun, he points it to himself without spinning its cylinder, and pulls the trigger. Calculate the probability of the first man's death.
Solution. Let A be the first man and B the second man. A is going to play the first, the third and the fifth round. The probability of A's death in the first round is
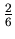 . If A survives, then in the second round B takes up the gun and if B survives, then in the third round A takes up the gun again. The probability of survival for A in the first round is
. If A survives, then in the second round B takes up the gun and if B survives, then in the third round A takes up the gun again. The probability of survival for A in the first round is
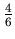 , and after that B has to survive in the second round. The probability of survival is
, and after that B has to survive in the second round. The probability of survival is
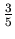 . Then the probability of A's death is
. Then the probability of A's death is
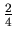 . Therefore the probability of the death of A in the third round is
. Therefore the probability of the death of A in the third round is
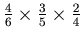 . Similarly the probability of the death of A in the fifth round is
. Similarly the probability of the death of A in the fifth round is
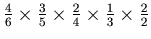 . Finally the probability of death of A is
. Finally the probability of death of A is
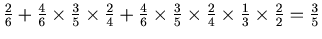 .
This is a very easy problem, but Miyadera suggested that it might be interesting to make the numbers of cylinders and bullets bigger. Then some students began to generalize the problem, and calculate the probabilities using almost the same method that they used in Example 1.
.
This is a very easy problem, but Miyadera suggested that it might be interesting to make the numbers of cylinders and bullets bigger. Then some students began to generalize the problem, and calculate the probabilities using almost the same method that they used in Example 1.
We denote by
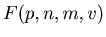 the probability of the death of the
the probability of the death of the 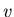 th player in this game when the gun has
th player in this game when the gun has 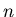 chambers and initially
chambers and initially 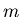 bullets in them when
bullets in them when 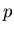 players participate the game.
players participate the game.
One of the authors (Sakaguchi) arranged
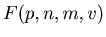 for
for
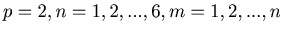 and
and 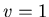 to make a triangle. Then he got the following Figure 1.
to make a triangle. Then he got the following Figure 1.
For example
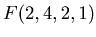 is the probability of the first man's death when
is the probability of the first man's death when
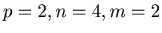 and
and 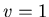 .
.
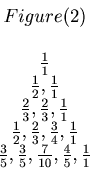
Then he calculated these probabilities by hands, and got the following Figure 2.
The value of
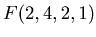 is
is
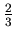 that is the second number in the fourth row.
that is the second number in the fourth row.
There seemed to be some kind of pattern in Figure 2, but the students could not find one. On the next day Sakaguchi discovered a very interesting pattern. He made a new triangle from Figure 2. This new triangle is Figure 3.
Figure 2 and 3 are mathematically the same. For example in Figure 2 the first fraction in the 4 th row is
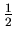 , and in Figure 3 the first fraction in the 4 th row is
, and in Figure 3 the first fraction in the 4 th row is
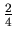
In Figure 3 the pattern is obvious. The list of the denominators and the list of the numerators of the fractions in Figure 3 form the same kind of pattern you can find in Pascal's triangle.
We are going to use Figure 4 to explain about the pattern. Figure 3 and Figure 4 consist of the same list of numbers, but in Figure 4 some fractions are in bold face to show the pattern. The second and the third fractions in the 4 th row are
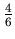 and
and
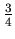 . The third fraction in the 5 th row is
. The third fraction in the 5 th row is
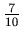 . The numerators are 3, 4, and 7, and we have 3 + 4 = 7. The denominators are 6, 4 and 10, and we have 6 + 4 = 10.
. The numerators are 3, 4, and 7, and we have 3 + 4 = 7. The denominators are 6, 4 and 10, and we have 6 + 4 = 10.
The students and the teacher were very happy when they discovered this Pascal like property of the triangle of numbers.
After students discovered this pattern, they began to use the computer algebra system Mathematica to study these Pascal like triangles.
One day two member of the authors (T.Hashiba and D.Minematsu) thought that it might be interesting to study the Russian roulette for more than 2 players. The teacher (Miyadera) thought that they would not find the Pascal like property in this genaralization of the Russian roulette, but he did not stop students. Computer algebra systems can calculate fractions, and hence students could study the problem with various values of numbers 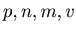 . By using the data that they got, the students and the teacher could make the general theory of Russian roulette.
. By using the data that they got, the students and the teacher could make the general theory of Russian roulette.
Finally they discovered that they could also make Pascal like triangles by the Russian roulette for more than 2 players.



: The mathematical background for
: pascal like triangles
: Abstract
Contents