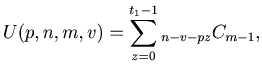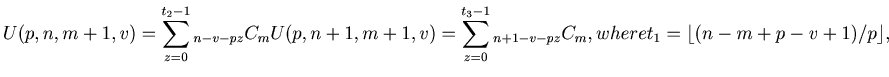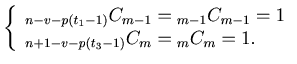


: Sierpinski like gaskets made
: pascal like triangles
: How students discovered Pascal
Contents
In this section we are going to study the mathematical background of Pascal like triangles.
First we are going to define the Russian roulette game and a mathematically equivalent game.
Definition 1: Let 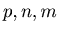 be fixed natural number such that
be fixed natural number such that 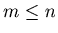 .
We have players
.
We have players
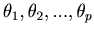 who are seated around a circle. The game begins with player
who are seated around a circle. The game begins with player
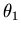 . Proceeding in order, a partially loaded revolver is passed from hand to hand. The gun has
. Proceeding in order, a partially loaded revolver is passed from hand to hand. The gun has 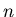 -chambers and initially
-chambers and initially 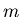 -bullets in them. When a player receives the gun, he points it to himself without spinning its cylinder,and pulls the trigger. If any player gets shot, he is the loser of the game and the game ends.
-bullets in them. When a player receives the gun, he points it to himself without spinning its cylinder,and pulls the trigger. If any player gets shot, he is the loser of the game and the game ends.
For some people the Russian roulette is not a good subject to study, and hence the authors present a mathematically equivalent game in Definition 2.
Definition 2: Let 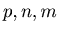 be fixed natural number such that
be fixed natural number such that 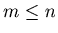 . We have players
. We have players
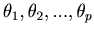 who are seated around a circle. The game begins with player
who are seated around a circle. The game begins with player
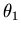 . Proceeding in order, a box is passed from hand to hand. The box contains n numbers. The numbers in the box are assigned in numerical order, from
. Proceeding in order, a box is passed from hand to hand. The box contains n numbers. The numbers in the box are assigned in numerical order, from 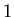 to
to 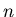 . When a player receive the box, he draws a number from the box. The players cannot see the numbers when they draw numbers, and hence they draw at random. Once a certain number was taken from the box, that number will not be returned to the box. If any player gets a number
. When a player receive the box, he draws a number from the box. The players cannot see the numbers when they draw numbers, and hence they draw at random. Once a certain number was taken from the box, that number will not be returned to the box. If any player gets a number 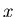 such that
such that 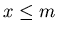 , he will be the loser of the game and the game ends.
, he will be the loser of the game and the game ends.
From now on the authors are going to use Definition 2 for the game they study in this article.
We denote by 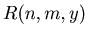 the probability of the game ends in the
the probability of the game ends in the 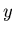 th round.
th round.
Lemma 1: For natural numbers 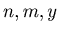 such that
such that
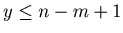 we have
we have
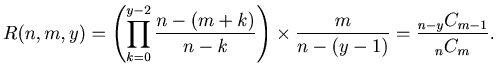 |
(1) |
Proof. If the game is to end in the 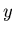 -th round, the players have to continue the game without becoming the loser from
the first round to the
-th round, the players have to continue the game without becoming the loser from
the first round to the 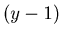 -th round. The probability to survive the first to the
-th round. The probability to survive the first to the 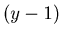 -th round are
-th round are
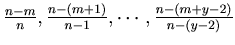 respectively and the probability of one of the
players loses in the
respectively and the probability of one of the
players loses in the 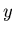 -th round is
-th round is
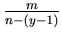 .
.
Therefore we have (1).
We are going to use the floor function. For any real number 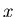 the function
the function
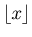 gives the greatest integer less than or equal to
gives the greatest integer less than or equal to 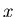 .
.
Theorem 1:
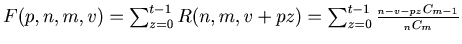 , where
, where
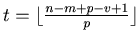 .
.
Proof.
Clearly the number of rounds is 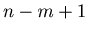 at most.
The
at most.
The 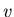 -th player plays the
-th player plays the 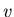 -th,
-th, 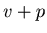 -th,
-th, 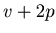 -th,
-th,
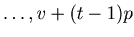 -th round, where
-th round, where 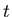 is the biggest natural number that satisfies
is the biggest natural number that satisfies
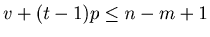 , and hence
, and hence
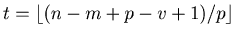 .
.
Therefore by Lemma 1
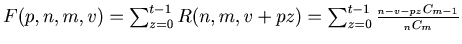 .
Definition 3: We define
.
Definition 3: We define
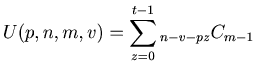 , where
, where
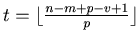 .
.
This number
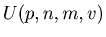 is important throughout this article. By Theorem 1 and Definition 3
is important throughout this article. By Theorem 1 and Definition 3
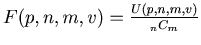 .
.
Lemma 2:
(1)
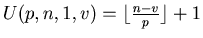 .
.
(2)
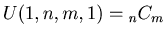 .
.
(3)
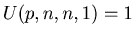 .
.
Proof. These equations are direct from Definition 3.
(1)
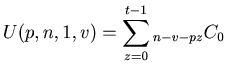
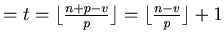 .
.
(2)
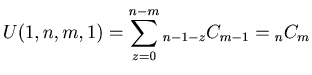 .
.
(3)
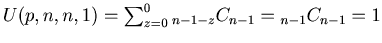 .
In the following Theorem 2 we are going to prove that
.
In the following Theorem 2 we are going to prove that
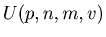 has the property that is very similar to the property of
has the property that is very similar to the property of 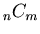 . To prove this we have only to use the well known formula
. To prove this we have only to use the well known formula
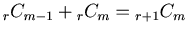 for each term of
for each term of
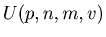 .
.
Theorem 2:
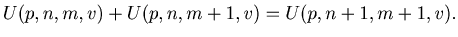
Proof. By Definition 3 we have
By (5) and (6) 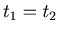 or
or
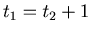 . We are going to deal with these two cases separately.
. We are going to deal with these two cases separately.
(a) If 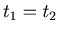 , by (2), (3), (4), (5), (6), (7) and (8) we have
, by (2), (3), (4), (5), (6), (7) and (8) we have
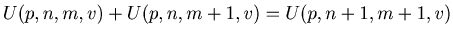 .
.
(b) If
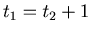 , then we have only to prove that the
, then we have only to prove that the 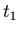 -th term of (2) is equal to the
-th term of (2) is equal to the 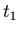 -th term of (4), since (3) does not have the
-th term of (4), since (3) does not have the 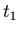 -th term.
-th term.
By the fact that
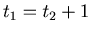 , we know that
, we know that 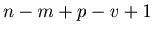 is a multiple of
is a multiple of 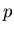 , and hence we have
, and hence we have
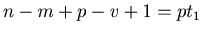 .
.
From this we have
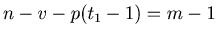
and
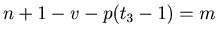 ,
,
which imply that
By (2), (3), (4), (5), (6), (7), (8) and (9) we have
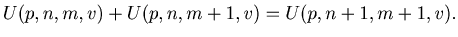 Remark. When
Remark. When 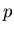 = 2, Theorem 2 was proved by one of the authors (Sakaguchi) when he was a high schoool student. See Sakaguchi, Miyadera and Masuda [3].
= 2, Theorem 2 was proved by one of the authors (Sakaguchi) when he was a high schoool student. See Sakaguchi, Miyadera and Masuda [3].
Theorem 2 was proved by two of the authors (Minamatsu and S.Hashiba) for any natural number 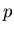 , when Hashiba was a high school student and Minematsu was a freshman in a university.
, when Hashiba was a high school student and Minematsu was a freshman in a university.
Although the teacher (Miyadera) helped them to make a proof, these students could prove the theorem almost by themselves.
By Theorem 2 and Lemma 2 (2)
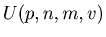 can be considered as a generalization of
can be considered as a generalization of 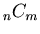 .
.
By Theorem 2 for fixed natural numbers 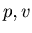 the list {
the list {
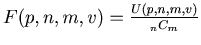 ,
, 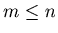 and
and  = 1,2,3,...} forms a pattern of fractions that is similar to Pascal's triangle.
= 1,2,3,...} forms a pattern of fractions that is similar to Pascal's triangle.



: Sierpinski like gaskets made
: pascal like triangles
: How students discovered Pascal
Contents
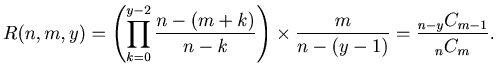
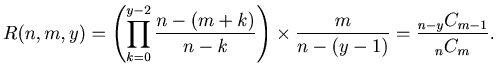
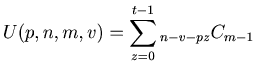 , where
, where
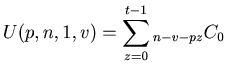
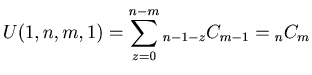 .
.