

: The Josephus Problem in both directions.
: The Self-Similarity of the Josephus Problem.
In this article we are going to study variants of the Josephus Problem and interesting properties of the graphs produced by these variants.
These variants have interesting recursive relations and beautiful self-similarities of the graphs.
The authors have studied variants of the Josephus Problem, and have published our result in [4], and our article is going to be published in [6].
In this article the authors are going to present new results of our research on the variants of the Josephus Problem.
With a proper computer program it becomes very easy to study this variant of the Josephus Problem. Please read the appendix of this article for the programs of the Josephus Problem.
First we are going to study the traditional Josephus Problem.
Definition 1.1
Let 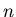 and
and 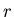 be natural numbers such that
be natural numbers such that 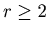 . We put
. We put 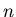 numbers in a circle, and we are going to remove numbers. We start counting up form the 1 st number, and the
numbers in a circle, and we are going to remove numbers. We start counting up form the 1 st number, and the 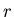 -th,
-th, 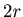 -th,
-th, 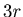 -th number, ... are to be removed. We denote by
-th number, ... are to be removed. We denote by 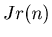 the position of the last number.
the position of the last number.
When 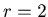 , then the function
, then the function 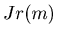 has very simple recursive relations.
has very simple recursive relations.
This is a well known formula. See [2].
Since 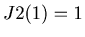 , by Theorem1.1 we can calculate
, by Theorem1.1 we can calculate 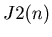 for any natural number
for any natural number 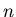 .
.
Example 1.1
The graph of the list {J2(n) , 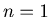 , 2, 3, ..., 100}.
, 2, 3, ..., 100}.
The horizontal coordinate is for the number of numbers involved in the game, and the vertical coordinate is for the last number. For example, by
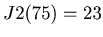 we have the point
we have the point 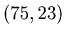 in the graph.
in the graph.
As you can see, the graph of the function 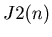 is very simple. It is interesting to compare this to the graphs in the following sections.
is very simple. It is interesting to compare this to the graphs in the following sections.


: The Josephus Problem in Both Directions
: The Self-Similarity of the Josephus Problem.
![]() , then the function
, then the function ![]() has very simple recursive relations.
has very simple recursive relations.