Next: Bibliography Up:Abstract and the table of contents Previous:Graphs for k = 2
First we study the chocolate in Fig. 7.6. You can cut this chocolate in three ways, and it is clear that the coordinates of this is {x,y,z}= {4,9,9}. This chocolate satisfies the inequalities ![]() . Note that y,z are non-negative integers.
. Note that y,z are non-negative integers.

Figure 7.6.
We divide the chocolate in Fig. 7.6 into the left part and the right part. The left part is in Fig 7.7 and the right part is in Fig. 7.8.
![]()
Figure 7.7
Figure 7.8
To study L-states of the chocolate in Fig 7.6 it is enough to study Grundy numbers of the chocolate in Fig. 7.8. The Grundy numbers generated by the chocolate in Fig 7.8 has a very simple mathematical structures. See Fig 7.9. The authors discovered this mathematical structure by calculations of Mathematica. It will not be difficult to prove the existence of this mathematical structure by mathematical induction, but the authors omit the proof here, since a complete proof will be lengthy.
Example 7.1 Mathematica program to create Fig 7.9.
Clear[allcases, move, Mex, Gr, gote, k, ss, res, pposition, ff, bl];
res[x_] := 2 Floor[x/2] + 1; res2[x_] := Max[2 Floor[x/2] - 2, 0];
inverseres2[x_] := Block[{dd}, dd = Table[m, {m, 0, 30}]; dd2 = Select[dd, res2[#] <= x &]; Max[dd2]];
ss = 22; al = Flatten[Table[{a, b}, {a, 0, ss}, {b, 0, ss}], 1];
allcases = Select[al, res[#[[1]]] >= #[[2]] >= res2[#[[1]]] &];
move[z_] := Block[{p}, p = z;
Union[Table[{t1, Min[res[t1], p[[2]]]}, {t1, 0, p[[1]] - 1}],
Table[{Min[inverseres2[p[[1]]], t2], t2}, {t2, 0, p[[2]] - 1}]
]
];
Mex[L_] := Min[Complement[Range[0, Length[L]], L]];
Gr[pos_] := Gr[pos] = Mex[Map[Gr, move[pos]]];
pposition = Select[allcases, Gr[#] == 0 &];
gg = 0.75;
ff[x_] := If[{x[[1]], x[[2]]} == {-1, -1}, "", If[x[[2]] == -1, x[[1]], If[x[[1]] == -1, x[[2]], If[res[x[[1]]] >= x[[2]] >= res2[x[[1]]], Gr[{x[[1]], x[[2]]}], ""]]]];
bl = Select[Flatten[Table[{n, m}, {n, 2, ss + 2}, {m, 1, res[ss] + 2}], 1], ! (res[#[[1]]] >= #[[2]] >= res2[#[[1]]]) &];
b2 = Table[{1, t}, {t, 2, ss + 3}]; b3 = Table[{t, 1}, {t, 2, ss + 1}]; a1 = {{2, 2}};
Grid[Table[ff[{n, m}], {n, -1, ss}, {m, -1, res[ss]}], Frame -> All, Background -> {None, None, Join[Table[bl[[s]] -> GrayLevel[0.87], {s, 1, Length[bl]}], Table[b3[[s]] -> GrayLevel[gg], {s, 1, Length[b3]}], Table[b2[[s]] -> GrayLevel[gg], {s, 1, Length[b2]}]]}]

Figure 7.9
We divide Grundy numbers in Fig 7.9 into three groups. The first group contains numbers that equal to 1 (mod 3). These numbers are printed in red squares. The second group contains numbers that equal to 2 (mod 3). These numbers are printed in blue squares. The third group contains numbers that equal to 0 (mod 3). These numbers are printed in white squares.
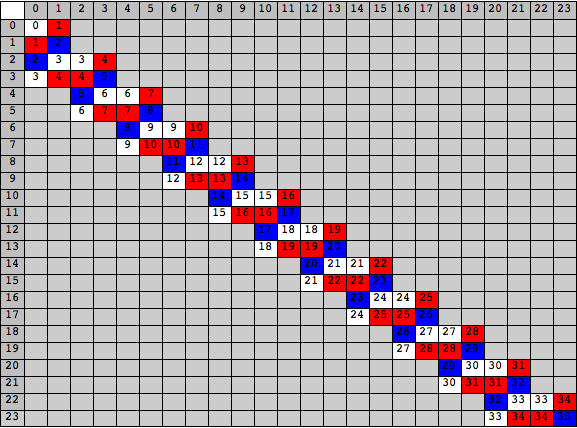
Figure 7.10
Here we study chocolate games that satisfy two inequalities ![]() .
.
First we study the chocolate in Fig. 7.11. You can cut this chocolate in three ways, and it is clear that the coordinates of this is {x,y,z}= {4,9,12}.
Figure 7.11
We divide the chocolate in Fig. 7.11 into the left part and the right part. The left part is in Fig 7.12 and the right part is in Fig. 7.13.
![]()
Figure 7.12

Figure 7.13
To study L-states of the chocolate in Fig 7.11 it is enough to study Grundy numbers of the chocolate in Fig. 7.13. The Grundy numbers generated by the chocolate in Fig 7.13 has a very simple mathematical structures. See Fig 7.14. The authors discovered this mathematical structure by calculations of Mathematica. It will not be difficult to prove the existence of this mathematical structure by mathematical induction, but the authors omit the proof here, since a complete proof will be lengthy.
Example 7.2 Mathematica program to create Fig 7.14.
Clear[allcases,move,Mex,Gr,gote,k,ss,pposition,ff,bl];k=1;h=3;
ss=30;al=Flatten[Table[{a,b},{a,0,ss},{b,0,ss}],1];
allcases=Select[al,(1/k)(#[[1]])≥#[[2]]≥(1/k)(#[[1]]-h)&];
move[z_]:=Block[{p},p=z;
Union[Table[{t1,Min[Floor[(1/k)(t1)],p[[2]]]},{t1,0,p[[1]]-1}],
Table[{Min[k*t2+h,p[[1]]],t2},{t2,0,p[[2]]-1}]
]
];
Mex[L_]:=Min[Complement[Range[0,Length[L]],L]];
Gr[pos_]:=Gr[pos]=Mex[Map[Gr,move[pos]]];
pposition=Select[allcases,Gr[#]==0&];
gg=0.75;
ff[x_]:=If[{x[[1]],x[[2]]}=={-1,-1},””,If[x[[2]]==-1,x[[1]],If[x[[1]]==-1,x[[2]],If[(1/k)x[[1]]≥x[[2]]≥(1/k)(x[[1]]-h),Gr[{x[[1]],x[[2]]}],” “]]]];
bl=Select[Flatten[Table[{n,m},{n,2,ss+2},{m,1,Floor[ss/k]+2}],1],!((1/k)#[[1]]≥#[[2]]≥(1/k)(#[[1]]-h))&];b2=Table[{1,t},{t,2,ss+2}];b3=Table[{t,1},{t,2,ss+2}];
Grid[Table[ff[{n,m}],{n,-1,ss},{m,-1,Floor[ss/k]}],Frame→All,Background→{None,None,Join[Table[bl[[s]]→GrayLevel[0.86],{s,1,Length[bl]}],Table[b3[[s]]→GrayLevel[gg],{s,1,Length[b3]}],Table[b2[[s]]→GrayLevel[gg],{s,1,Length[b2]}]]}]

Figure 7.14
We divide Grundy numbers in Fig 7.14 into three groups. The first group contains numbers that equal to 1 (mod 3). These numbers are printed in red squares. The second group contains numbers that equal to 2 (mod 3). These numbers are printed in blue squares. The third group contains numbers that equal to 0 (mod 3). These numbers are printed in white squares.
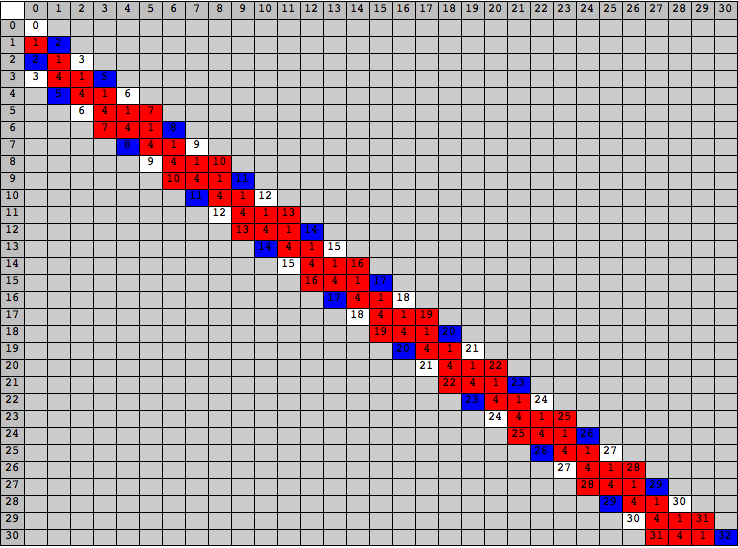
Figure 7.15
Next: Bibliography Up:Abstract and the table of contents Previous: