Shunsuke Nakamura, Ryo Hanafusa, Wataru Ogasa, Takeru Kitagawa and Ryohei Miyadera
We study chocolate games that are variants of a game of Nim. We can cut the chocolate games in 3 directions, and we represent the chocolates with coordinates
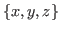
, where
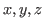
are the maximum times you can cut them in each direction.
The coordinates
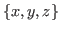
of the chocolates satisfy the inequalities
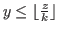
for
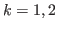
.
For
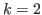
we prove a theorem for the L-state (loser's state), and the proof of this theorem can be easily generalized to the case of an arbitrary even number
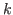
.
For
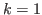
we prove a theorem for the L-state (loser's state), and we need the theory of Grundy numbers to prove the theorem. The generalization of the case of
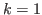
to the case of an arbitrary odd number is an open problem.
The authors present beautiful graphs made by Grundy numbers of these chocolate games.
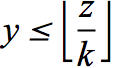 for k=1,2
and Grundy numbers
for k=1,2
and Grundy numbers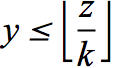 for k=1,2
and Grundy numbers
for k=1,2
and Grundy numbers