Next: Some definitions
Up:Abstract and the table of contents Previous: The structure of rows
The structure of each column
Here we study the structure of each column.
Next we study the mathematical structure of a column generally.
Prediction 5.5
When 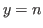 , then the number at the top of the column is
, then the number at the top of the column is
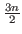
 if
if 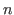 is even
is even 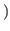 and
and
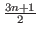
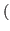 if
if 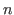 is odd
is odd 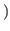 .
.
If we start with the number on the top of the column and move down picking up every other number, then we have an arithmetic sequence with common difference of 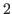 .
.
On the other hand if we start with 1 that is the second number from the top of the column and move down picking up every other number, then we have
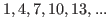 that is an arithmetic sequences with common difference of
that is an arithmetic sequences with common difference of 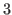 whose length is
whose length is
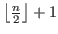 , and after that the sequence becomes an arithmetic sequences with common difference of
, and after that the sequence becomes an arithmetic sequences with common difference of 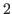 .
.
Next: Some definitions
Up:Abstract and the table of contents Previous: The structure of rows
![\includegraphics[height=9cm]{k1grundyvertical.eps}](img412.png)