Next: Structure of row
Up:Abstract and the table of contents Previous: To divide chocolates
The Chocolates that satisfy the inequality 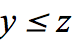 .
.
In this section we study the chocolate of Fig 5.1. The mathematical structure of this chocolate is interesting when it is compared to that of chocolate of Definition 2.4. While the chocolate of Definition 2.4 has a simple formula for L-states, this chocolate has complicated formulas for L-states.
![\includegraphics[height=3.3cm]{k1demo.eps}](img281.png)
The list of L-states of the game with inequality 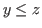 is the union of the following lists
is the union of the following lists  ,
,  ,
, 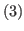 ,
, 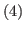 ,
, 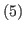 and
and 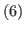 .
.
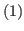
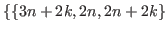 ,
,
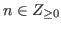 and
and 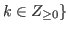
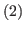
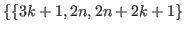 ,
,
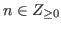 and
and 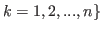
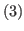
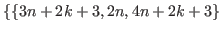 ,
,
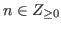
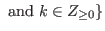
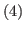
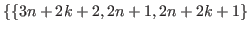 ,
,
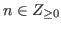 and
and 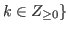
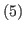
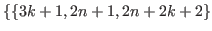 ,
,
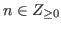 and
and 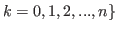
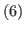
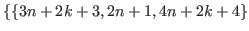 ,
,
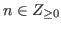 and
and 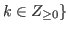 .
The above facts are proved in Theorem 5.1.
The proofs for the case of
.
The above facts are proved in Theorem 5.1.
The proofs for the case of 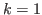 are presented in this article for the first time. The logic behind proofs is simple, but is is extremely difficult to present a complete proof. In fact there are too many cases that need to be treated. The authors present several typical cases to be proved, and omit other cases. They think that it is not difficult to treat other cases in a method that is similar to the one used in these typical cases.
are presented in this article for the first time. The logic behind proofs is simple, but is is extremely difficult to present a complete proof. In fact there are too many cases that need to be treated. The authors present several typical cases to be proved, and omit other cases. They think that it is not difficult to treat other cases in a method that is similar to the one used in these typical cases.
We define a new type of chocolate precisely.
Definition 5.1
There is a blue
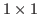 block, and on both side of it there are columns of brown blocks that are numbered by integers. In the chocolate in Fig. 5.1 we have the first, the second, the fourth,...,10th column on the right side of the blue block and
block, and on both side of it there are columns of brown blocks that are numbered by integers. In the chocolate in Fig. 5.1 we have the first, the second, the fourth,...,10th column on the right side of the blue block and 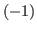 th,
th, 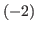 th,...,
th,...,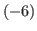 th column on the left side of the blue block.
th column on the left side of the blue block.
The i-th column is
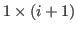 block for
block for
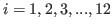 and the i-th column is
and the i-th column is
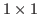 block for
block for
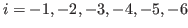 .
.
By generalizing the chocolate in Fig. 5.1 we make a chocolate that has the first, the second, the fourth,...,n-th column,... on the right side of the blue block and 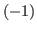 th,
th, 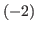 th,...,
th,...,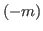 -th column,... on the left side of the blue block.
-th column,... on the left side of the blue block.
The i-th column is
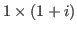 block for
block for
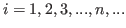 and the i-th column is
and the i-th column is
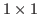 block for
block for
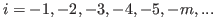 .
.
Brown blocks are sweet chocolate that can be eaten, and the blue block is the bitter chocolate that cannot be eaten.
You can cut these chocolate along the segments in three ways.
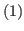 You cut vertically on the left side of the blue (bitter) block.
You cut vertically on the left side of the blue (bitter) block.
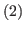 You cut horizontally above the blue (bitter) block.
You cut horizontally above the blue (bitter) block.
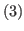 You cut vertically on the right side of the blue (bitter) block.
You cut vertically on the right side of the blue (bitter) block.
Therefore it is proper to represent this chocolate with 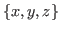 , where
, where 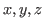 stand for the maximum numbers of times that we can cut these chocolate in each direction. For example in Fig. 5.1 we can cut 6 times at most vertically on the left side of the blue block, we can cut 10 times at most horizontally above the blue (bitter) block and we can 10 times at most vertically on the right side of the blue block. Therefore
stand for the maximum numbers of times that we can cut these chocolate in each direction. For example in Fig. 5.1 we can cut 6 times at most vertically on the left side of the blue block, we can cut 10 times at most horizontally above the blue (bitter) block and we can 10 times at most vertically on the right side of the blue block. Therefore 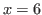 ,
, 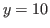 and
and 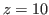 . Therefore we represent the chocolate in Fig. k1demochoco with the coordinates
. Therefore we represent the chocolate in Fig. k1demochoco with the coordinates
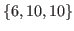 .
.
For any
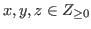 we denote by
we denote by 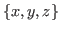 the state of chocolate.
We study the chocolate in Fig. 5.2 to calculate L-states of the chocolate game in Fig. 5.1. In Fig. 5.2
If you can cut horizontally above the blue (bitter) block
the state of chocolate.
We study the chocolate in Fig. 5.2 to calculate L-states of the chocolate game in Fig. 5.1. In Fig. 5.2
If you can cut horizontally above the blue (bitter) block 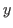 times at most and
vertically on the right side of the blue (bitter) block
times at most and
vertically on the right side of the blue (bitter) block 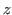 times at most, then we represent the chocolate with the coordinates
times at most, then we represent the chocolate with the coordinates 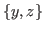 .
.
![\includegraphics[height=3.3cm]{yzgrundychoco.eps}](img342.png)
Fig 5.3 is the table of Grundy numbers of the chocolate in 5.2 for
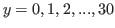 and
and
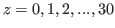 .
.
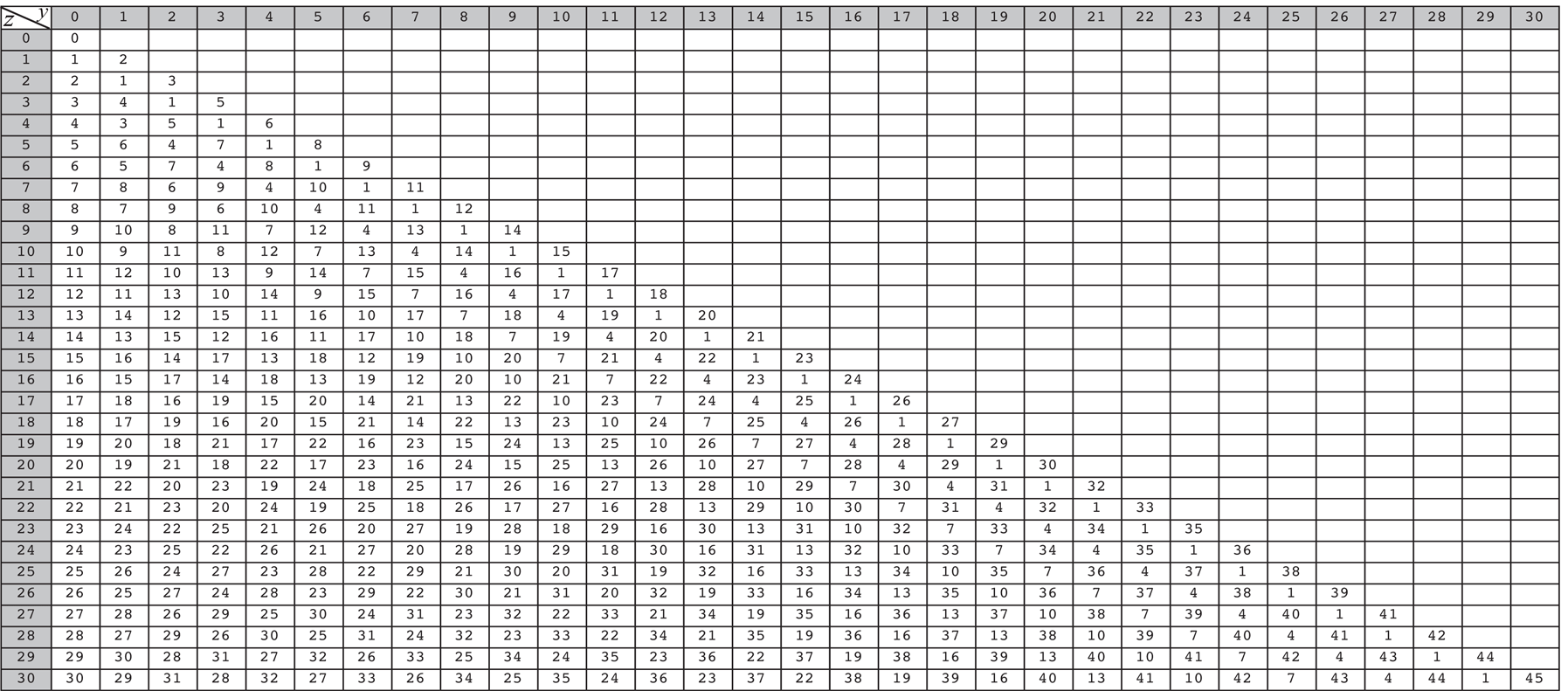
In Fig 5.3 there are many kinds of mathematical structures, but in this section we study the structures of each row and column of the table of Grundy numbers.
Subsections
Next: Structure of row
Up:Abstract and the table of contents Previous: To divide chocolates
![\includegraphics[height=3.3cm]{k1demo.eps}](img281.png)
![]() is the union of the following lists
is the union of the following lists ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
![]()
![]() ,
,
![]() and
and ![]()
![]()
![]() ,
,
![]() and
and ![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() and
and ![]()
![]()
![]() ,
,
![]() and
and ![]()
![]()
![]() ,
,
![]() and
and ![]() .
The above facts are proved in Theorem 5.1.
The proofs for the case of
.
The above facts are proved in Theorem 5.1.
The proofs for the case of ![]() are presented in this article for the first time. The logic behind proofs is simple, but is is extremely difficult to present a complete proof. In fact there are too many cases that need to be treated. The authors present several typical cases to be proved, and omit other cases. They think that it is not difficult to treat other cases in a method that is similar to the one used in these typical cases.
are presented in this article for the first time. The logic behind proofs is simple, but is is extremely difficult to present a complete proof. In fact there are too many cases that need to be treated. The authors present several typical cases to be proved, and omit other cases. They think that it is not difficult to treat other cases in a method that is similar to the one used in these typical cases.
![\includegraphics[height=3.3cm]{yzgrundychoco.eps}](img342.png)
