Next: Case 4
Up:Abstract and the table of contents Previous: Case 2
Case 3
Next we study the case that 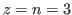
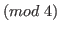 and
and 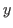 is odd.
is odd.
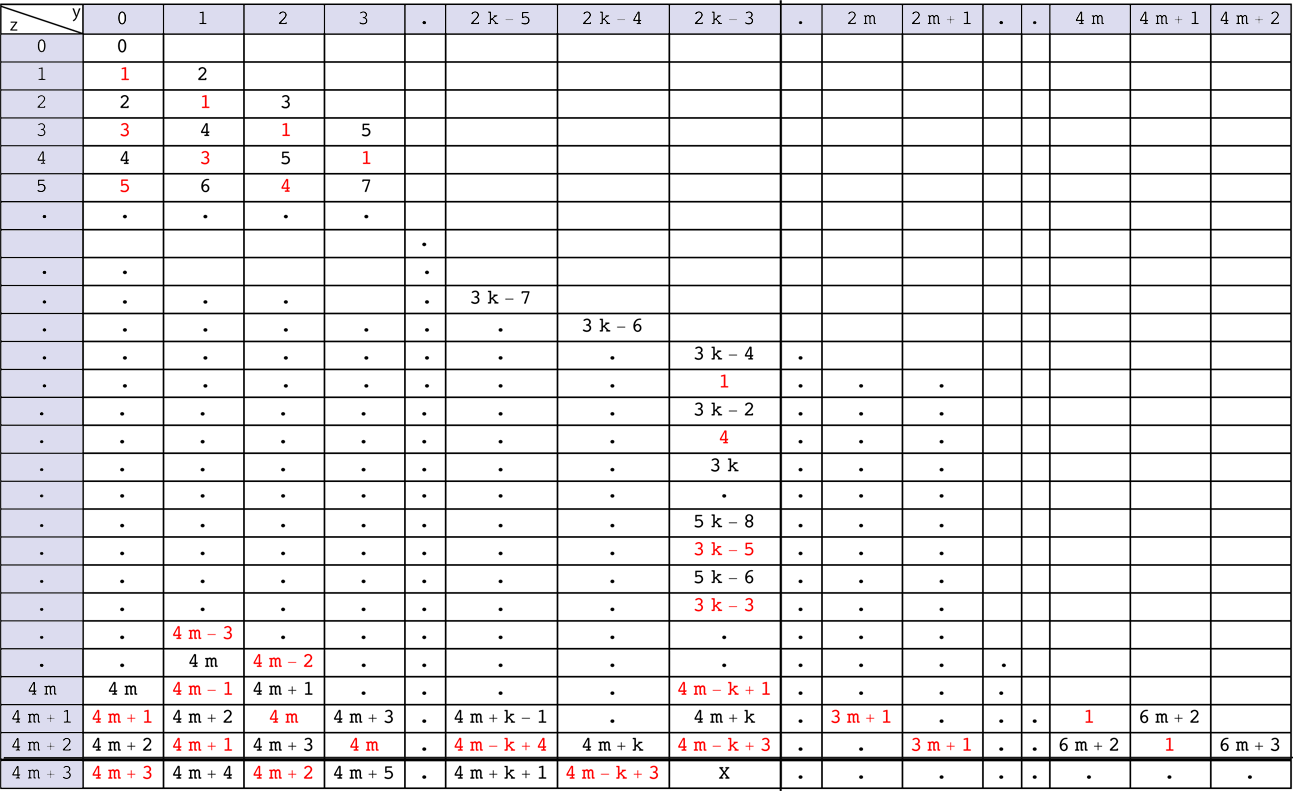
In this subsection we use methods that are very similar to the one used in Subsection 5.4.2 and Subsection 5.4.3, and hence we omit the detail of the argument.
In Fig. 5.21 we suppose that Predictions 5.1, 5.2, 5.3,5.4 and 5.5 are valid for
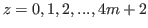 and for
and for
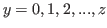 . We also suppose that these predictions are valid for
. We also suppose that these predictions are valid for 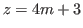 and
and
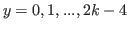 . Under these assumptions we prove that
. Under these assumptions we prove that
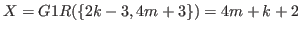 .
.
For
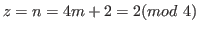 by Prediction 5.1 the first number from the right end of the row is
by Prediction 5.1 the first number from the right end of the row is 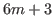 .
.
We suppose that
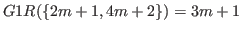 |
(5.51) |
and
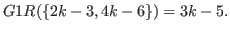 |
(5.52) |
We also assume that
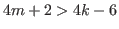 and and 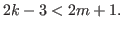 |
(5.53) |
If we are to prove that
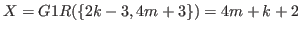 , by Lemma 5.1 we have only to prove that
, by Lemma 5.1 we have only to prove that 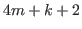 is the smallest number that does not belong to
is the smallest number that does not belong to
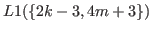 .
.
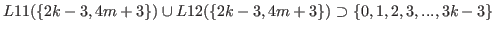 .
.
We have
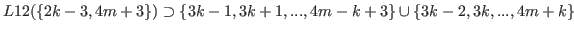
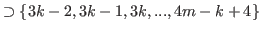 .
.
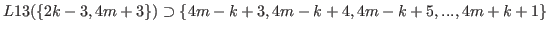 .
Therefore we have
.
Therefore we have 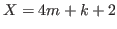 .
.
The case that 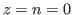
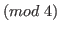 can be treated in the similar way, so we omit it.
can be treated in the similar way, so we omit it.
Next: Case 4
Up:Abstract and the table of contents Previous: Case 2

