Next: Case 3
Up:Abstract and the table of contents Previous: Case 1
Case 2
In this subsection we study the case that
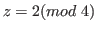 and
and 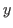 is odd.
is odd.
An example of this case is Example 5.4.
The argument here looks complicated, but it is a generalization of argument used in Example 5.4
. 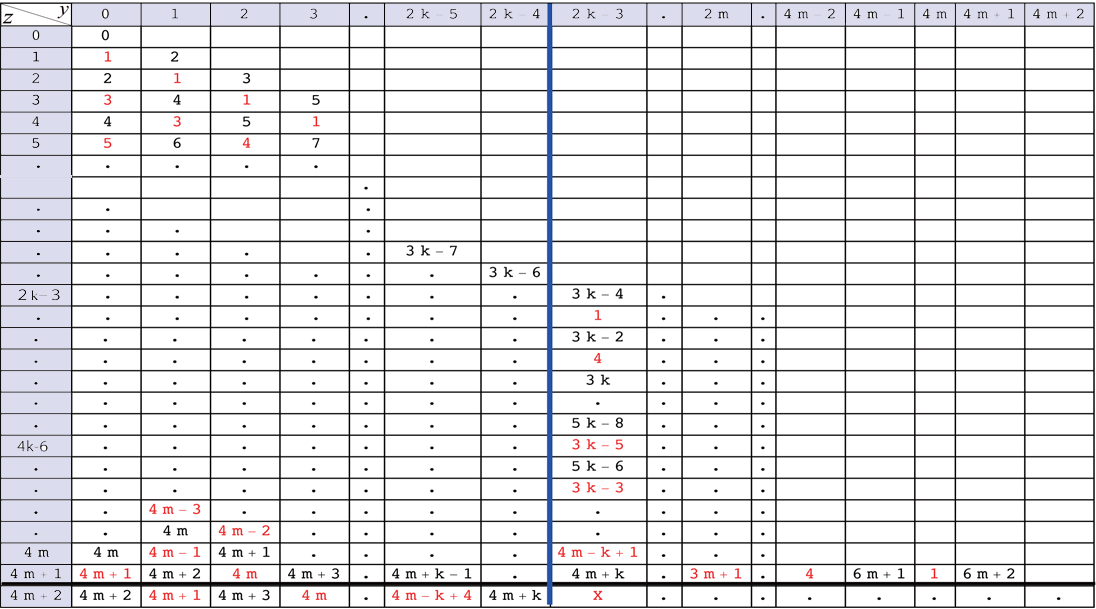
In Fig. 5.20 we suppose that Predictions 5.1, 5.2, 5.3,5.4 and 5.5 are valid for
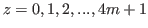 and for
and for
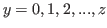 . We also suppose that these predictions are valid for
. We also suppose that these predictions are valid for 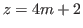 and
and
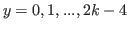 . Under these assumptions we prove that
. Under these assumptions we prove that
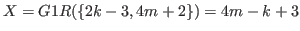 .
.
For
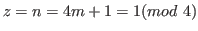 by Prediction 5.1 the first number from the right end of the row is
by Prediction 5.1 the first number from the right end of the row is 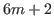 .
If we start with
.
If we start with 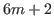 and go leftward picking up every other number, then we have
and go leftward picking up every other number, then we have
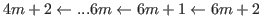 which is an arithmetic sequence with common difference of
which is an arithmetic sequence with common difference of 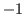 .
.
On the other hand if we start with 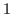 that is the second number from the right end of the row and go leftward picking up every other number, then we have an arithmetic sequence with common difference of
that is the second number from the right end of the row and go leftward picking up every other number, then we have an arithmetic sequence with common difference of 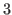 whose length is
whose length is
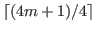
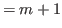 , and hence the last number of this sequence is
, and hence the last number of this sequence is
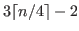
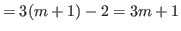 . This number
. This number 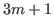 is the first number of an arithmetic sequence with common difference of
is the first number of an arithmetic sequence with common difference of 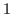 and the last number of this sequence is
and the last number of this sequence is 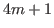 .
.
By Prediction 5.5 for
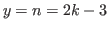 the number at the top of the column is
the number at the top of the column is
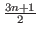
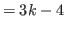 . If we move down picking up every other number, then we have an arithmetic sequence with common difference of
. If we move down picking up every other number, then we have an arithmetic sequence with common difference of 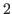 .
.
On the other hand if we start with 1 that is the second number of the column and move down picking up every other number, then we have
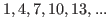 that starts as an arithmetic sequence with common difference of
that starts as an arithmetic sequence with common difference of 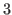 such that it has
such that it has
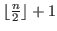
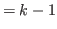 terms and the last number is
terms and the last number is
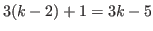 , then it becomes an arithmetic sequence with common difference of
, then it becomes an arithmetic sequence with common difference of 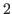 whose first number is
whose first number is 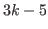 .
.
In Fig. 5.20 we suppose that
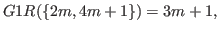 |
(5.42) |
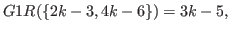 |
(5.43) |
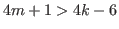 and and 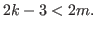 |
(5.44) |
By Lemma 5.1 we have only to prove that 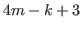 is the smallest number that does not belong to
is the smallest number that does not belong to
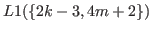 to get
to get
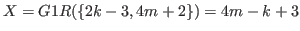 .
.
By Definition 5.2
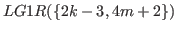 can be separated into three parts
can be separated into three parts
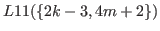 ,
,
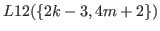 and
and
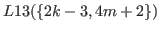 .
.
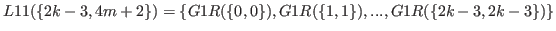
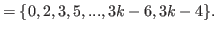 |
(5.45) |
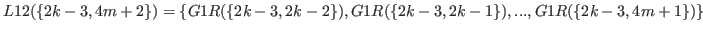
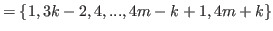
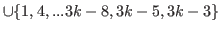 |
(5.46) |
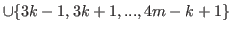 |
(5.47) |
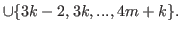 |
(5.48) |
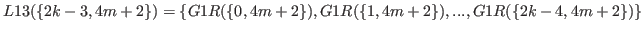
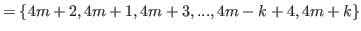
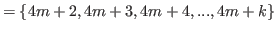 |
(5.49) |
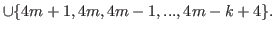 |
(5.50) |
By (5.45) and (5.46) we have
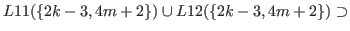
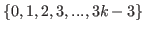 .
.
By (5.49) and (5.50) all the numbers in
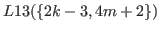 are bigger than
are bigger than 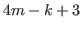 .
.
By (5.47) and (5.48)
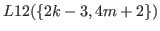
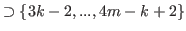 .
We know that the list
.
We know that the list
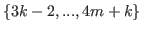 does not contain
does not contain 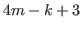 , since the numbers in
the list and the number
, since the numbers in
the list and the number 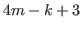 have opposite parity.
have opposite parity. 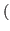 In other words if
In other words if 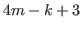 is odd, then the numbers in the list are even, and if
is odd, then the numbers in the list are even, and if 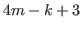 is even, then the numbers in the list are odd.
is even, then the numbers in the list are odd. 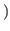 .
Therefore we have
.
Therefore we have 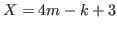 .
.
Next: Case 3
Up:Abstract and the table of contents Previous: Case 1

![]()
![]() .
.
![]() are bigger than
are bigger than ![]() .
.
![]()
![]() .
We know that the list
.
We know that the list
![]() does not contain
does not contain ![]() , since the numbers in
the list and the number
, since the numbers in
the list and the number ![]() have opposite parity.
have opposite parity. ![]() In other words if
In other words if ![]() is odd, then the numbers in the list are even, and if
is odd, then the numbers in the list are even, and if ![]() is even, then the numbers in the list are odd.
is even, then the numbers in the list are odd. ![]() .
Therefore we have
.
Therefore we have ![]() .
.