Next: Case 1
Up:Abstract and the table of contents Previous: The structure of Grundy numbers
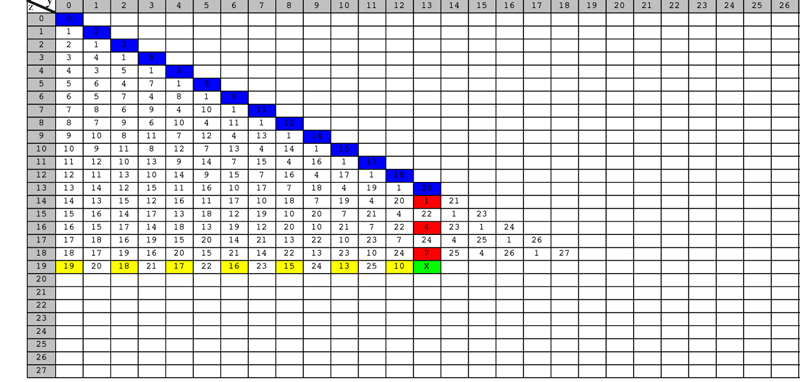
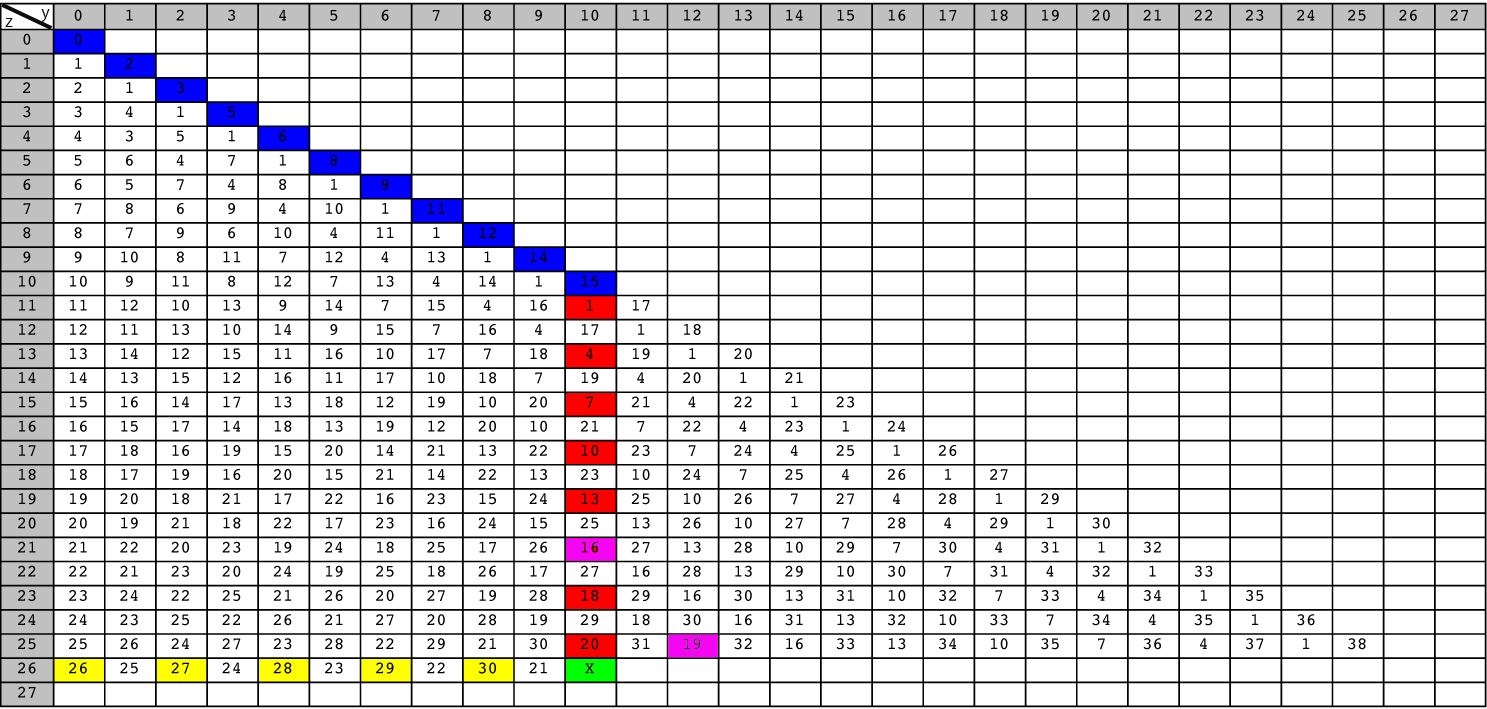
Here are some examples to show how to calculate Grundy numbers.
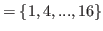 |
(5.2) |
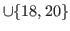 |
(5.3) |
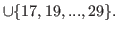 |
(5.4) |
The numbers of
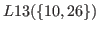 are in yellow or white rectangles.
are in yellow or white rectangles.
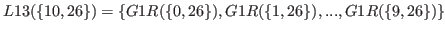
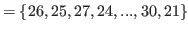
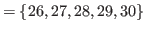 |
(5.5) |
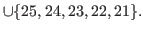 |
(5.6) |
By (5.1) and (5.2) we have
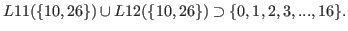 |
(5.7) |
By (
5.3) and (
5.4)
we have
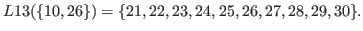 |
(5.9) |
By (5.4), (5.7), (5.8) and (5.9) we have
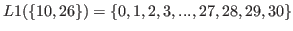 , and
, and 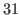 is the smallest number that does not belong to
is the smallest number that does not belong to
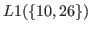 . Therefore
. Therefore
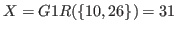 .
.
Remark 5.1
In Fig. 5.15 the positions of
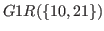 and
and
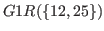 have important role. These Grundy numbers are in purple rectangles.
have important role. These Grundy numbers are in purple rectangles.
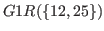 is the last term in the arithmetic sequence of common difference of 3 in the row when
is the last term in the arithmetic sequence of common difference of 3 in the row when 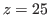 , and
, and
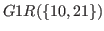 is the last term in the arithmetic sequence of common difference of 3 in the column when
is the last term in the arithmetic sequence of common difference of 3 in the column when 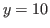 . Since these numbers are the last term of arithmetic sequence of common difference of 3, the calculation of
. Since these numbers are the last term of arithmetic sequence of common difference of 3, the calculation of
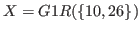 is easy by the fact that
is easy by the fact that
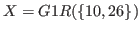 is under Grundy number
is under Grundy number
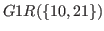 and it is on the right side of Grundy number
and it is on the right side of Grundy number
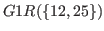 .
.
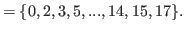 |
(5.10) |
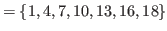 |
(5.11) |
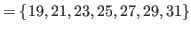 |
(5.12) |
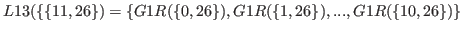
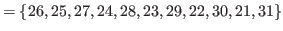
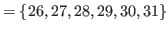 |
(5.13) |
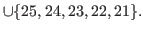 |
(5.14) |
By (5.10) and (5.11)
we have
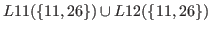
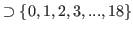 .
.
By (5.13) and (5.14) all the numbers in
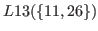 are bigger than
are bigger than 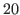 .
.
By (5.12)
we have
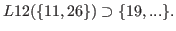 Note that the list {19,21,23,25,27,29,31} does not contain
Note that the list {19,21,23,25,27,29,31} does not contain 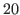 . Therefore we have
. Therefore we have 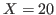 . A very important fact is that the numbers in
the list and the number
. A very important fact is that the numbers in
the list and the number 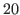 have opposite parity. This fact play an important role when we prove predictions generally.
have opposite parity. This fact play an important role when we prove predictions generally.
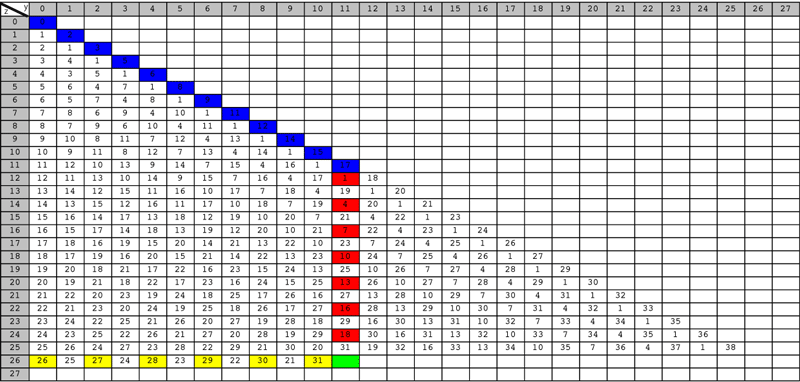
Example 5.5
We show the method to find the value of 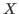 in Fig. 5.17 that is a table of Grundy numbers of the chocolate game with the inequality
in Fig. 5.17 that is a table of Grundy numbers of the chocolate game with the inequality 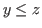 .
.
To find the value of
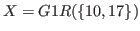 we have only to find the smallest number that does not belong to
we have only to find the smallest number that does not belong to
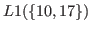
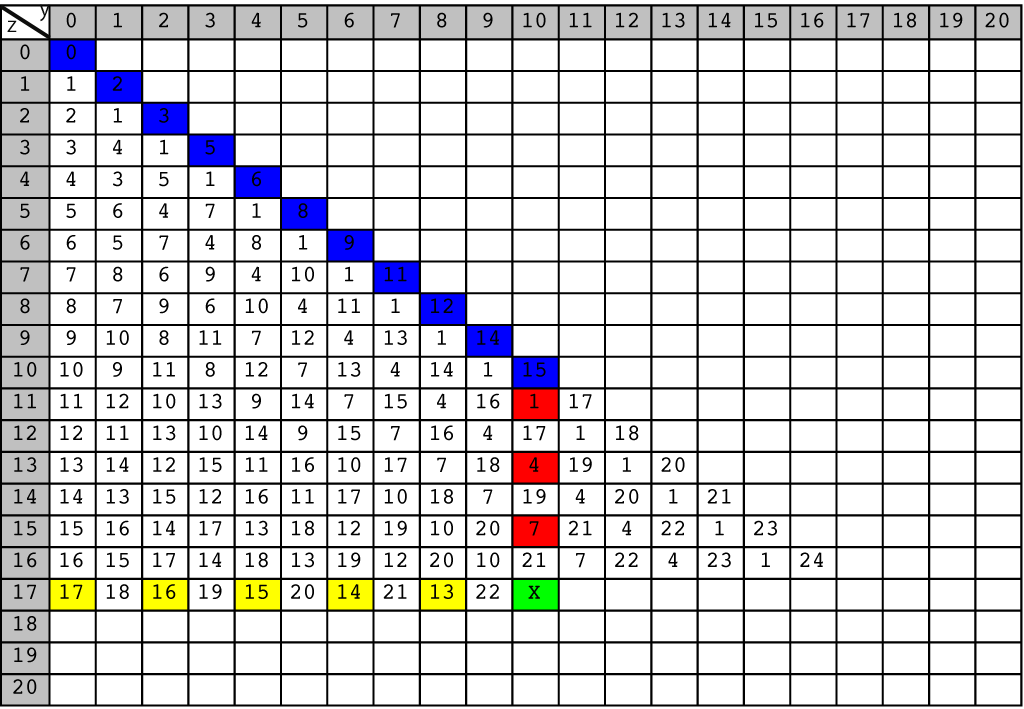
Remark 5.2
Note that
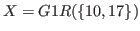 is in the midst of the the sequence
is in the midst of the the sequence
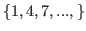 in the column for
in the column for 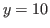 , and this condition make this example different from Example 5.3 and Example 5.4.
, and this condition make this example different from Example 5.3 and Example 5.4.
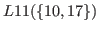
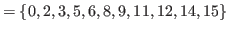
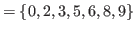 |
(5.15) |
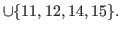 |
(5.16) |
Clearly
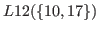
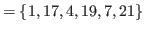
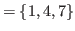 |
(5.17) |
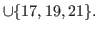 |
(5.18) |
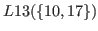
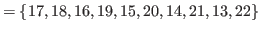
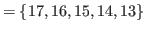 |
(5.19) |
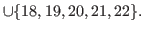 |
(5.20) |
By (5.15) and (5.17) we have
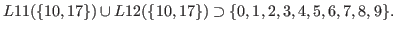 |
(5.21) |
By (5.16), (5.18), (5.19) and (5.20)
The lists
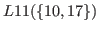 ,
,
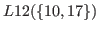 and
and
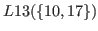 do not contain
do not contain 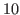 , and hence we have
, and hence we have
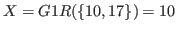 .
.
Next: Case 1
Up:Abstract and the table of contents Previous: The structure of Grundy numbers
![]() can be separated into three parts
can be separated into three parts
![]() ,
,
![]() and
and
![]() .
.
![]() are in blue rectangles.
are in blue rectangles.
![]()

![]() can be separated into three parts
can be separated into three parts
![]() ,
,
![]() and
and
![]() .
.
![]() are in blue rectangles.
are in blue rectangles.
![]()
![]() in Fig. 5.17 that is a table of Grundy numbers of the chocolate game with the inequality
in Fig. 5.17 that is a table of Grundy numbers of the chocolate game with the inequality ![]() .
.
![]() we have only to find the smallest number that does not belong to
we have only to find the smallest number that does not belong to
![]()

![]() ,
,
![]() and
and
![]() do not contain
do not contain ![]() , and hence we have
, and hence we have
![]() .
.