Next: Chocolate games for k
Up: Abstract and the table of contents
Previous: Introduction
Chocolate games that satisfy the inequality 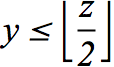 .
.
Next we define chocolate games. Please consult chocolates in Fig.2.1 and Fig.2.2 while you read this definition, since this definition looks very abstract without examples.
Definition 2.1
The chocolate consists of square boxes, and only one block is blue and others are brown.
Brown blocks are sweet and the blue block is very bitter. This game is played by two players in turn.
Each player breaks the chocolate (in a straight line along the blue line) into two area.
The player eats the area that does not contain blue block. The player who breaks the chocolate and eats to leave his opponent with the single bitter block (blue block) is the winner.
Remark 2.1
Note that in Definition
 we are not considering a misere play, since the player who breaks the chocolate for the last time is the winner, since his opponent cannot break the remaining blue (bitter) block. Therefore the chocolate games in this article are normal play games.
we are not considering a misere play, since the player who breaks the chocolate for the last time is the winner, since his opponent cannot break the remaining blue (bitter) block. Therefore the chocolate games in this article are normal play games.
Example 2.1
The chocolate of Fig.
 is proposed by Robin [1], and the chocolate of Fig.
is proposed by Robin [1], and the chocolate of Fig.
 is a new game proposed by the authors.
is a new game proposed by the authors.

![\includegraphics[height=2.5cm]{choco1203b.eps}](img270.png)
When we study the chocolate games, there are two important states of chocolates.
Definition 2.2
Here we define two important states of chocolates.
 W-states, from which we can force a win, as long as we play correctly at every stage.
W-states, from which we can force a win, as long as we play correctly at every stage.
 L-states, from which we will lose however well we play, but we may end up winning if our opponents make a mistake.
L-states, from which we will lose however well we play, but we may end up winning if our opponents make a mistake.
It is important to realize that the outcome of this game is not pre-determined, but there is nothing that the potential loser can do if the potential winner plays correctly at ever stage. However the potential winner cannot afford to make a single mistake, for if he does, then his opponent can exploit this.
One of the most important topics of chocolate games is to find all the L-states and the W-states of games. We denote by
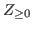 the set of non-negative integers.
the set of non-negative integers.
Remark 2.2
For the L-states of the chocolate of Fig. 2.1 see the problem corner in [1]. See also Theorem 7.12 in [2] (p-138). Note that in [2] they use the term "P-position" instead of "L-state" of this article.
We define nim-sum that is important for the theory of games.
This is a well known result of nim-sum. For a proof see Theorem 7.12 in [2] (p-139).
We generalize the chocolate games in Fig. 2.2, and define the chocolate game that we study in this article.
Definition 2.4
There is a blue
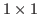 block, and on both side of it there are columns of brown blocks that are numbered by integers. In the chocolate in Fig. 2.3 we have the first, the second, the fourth,...,12th column on the right side of the blue block and
block, and on both side of it there are columns of brown blocks that are numbered by integers. In the chocolate in Fig. 2.3 we have the first, the second, the fourth,...,12th column on the right side of the blue block and 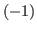 th,
th, 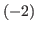 th,...,
th,...,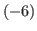 th column on the left side of the blue block.
th column on the left side of the blue block.
The i-th column is
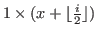 block for
block for
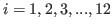 and the i-th column is
and the i-th column is 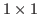 block for
block for
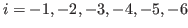 .
.
The generalization of the chocolate in Fig. 2.3 is the chocolate in Fig. 2.4. In this chocolate we have the first, the second, the fourth,...,n-th column,... on the right side of the blue block and 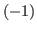 th,
th, 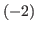 th,...,
th,...,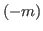 -th column,... on the left side of the blue block.
-th column,... on the left side of the blue block.
The i-th column is
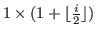 block for
block for
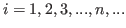 and the i-th column is
and the i-th column is
 block for
block for
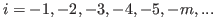 .
.
Brown blocks are sweet chocolate that can be eaten, and the blue block is the bitter chocolate that cannot be eaten.
![\includegraphics[height=2.8cm]{choco1203b3.eps}](img52.png)
![\includegraphics[height=3.3cm]{choco1203b2.eps}](img53.png)
You can cut these chocolate along the segments in three ways.
 You cut vertically on the left side of the blue (bitter) block.
You cut vertically on the left side of the blue (bitter) block.
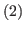 You cut horizontally above the blue (bitter) block.
You cut horizontally above the blue (bitter) block.
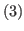 You cut vertically on the right side of the blue (bitter) block.
You cut vertically on the right side of the blue (bitter) block.
Therefore it is proper to represent this chocolate with 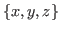 , where
, where 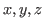 stand for the maximum numbers of times that we can cut these chocolate in each direction. For example in Fig. 2.3 we can cut 6 times at most vertically on the left side of the blue block, we can cut 6 times at most horizontally above the blue (bitter) block and we can 12 times at most vertically on the right side of the blue block. Therefore
stand for the maximum numbers of times that we can cut these chocolate in each direction. For example in Fig. 2.3 we can cut 6 times at most vertically on the left side of the blue block, we can cut 6 times at most horizontally above the blue (bitter) block and we can 12 times at most vertically on the right side of the blue block. Therefore 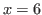 ,
, 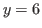 and
and 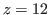 . Therefore we represent the chocolate in Fig. 2.3 with the coordinates
. Therefore we represent the chocolate in Fig. 2.3 with the coordinates
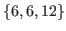 .
.
For any
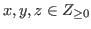 we denote by
we denote by 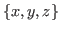 the state of chocolate.
the state of chocolate.
Example 2.2
Here we have four examples of states of chocolates that appear when we play the chocolate game of Fig. 2.5
![\includegraphics[height=1.5cm]{choco2yz.eps}](img59.png)
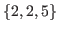
![\includegraphics[height=1.5cm]{choco2yzcut1.eps}](img60.png)
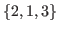
![\includegraphics[height=1.5cm]{choco2yzcut2.eps}](img61.png)
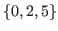
It is clear that the coordinates of these states satisfy the inequality 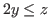 , and this is equivalent to the inequality
, and this is equivalent to the inequality
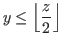 |
(2.2) |
where
 is the floor function. Note that
is the floor function. Note that
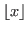 is the largest integer not greater than
is the largest integer not greater than 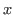 for any real number
for any real number 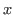 .
.
Note that you can cut
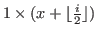 block
horizontally
block
horizontally
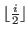 times at most for any non-negative integer
times at most for any non-negative integer 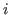 .
.
Inequality (2.2) is important to understand the structure of the chocolate. If you start with the chocolate in Fig. 2.5 and reduce the third coordinate 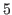 to
to 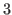 by cutting vertically on the right side of the bitter block, then by the structure of the chocolate the second coordinate is reduced to
by cutting vertically on the right side of the bitter block, then by the structure of the chocolate the second coordinate is reduced to 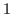 .
.
In this way we get the chocolate in Fig. 2.6.
If we are to explain the move from the chocolate in Fig. 2.5 to the chocolate in Fig. 2.6 using Inequality (2.2), we use the following explanation.
Let 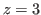 , then by Inequality (2.2) we get
, then by Inequality (2.2) we get 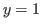 .
.
Proof
When we write 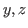 in base 2,
in base 2, 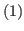 and
and 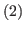 of this lemma is clear from the definition of floor function
of this lemma is clear from the definition of floor function
 .
.
Proof
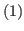 and
and 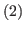 are direct from Lemma 2.1 and the Definition 2.3 of nim-sum.
are direct from Lemma 2.1 and the Definition 2.3 of nim-sum.
Remark 2.3
Suppose that
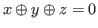 and
and
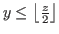 . Then there exists
. Then there exists
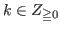 such that (2.5) is valid for
such that (2.5) is valid for
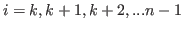 , and by using
(2.6) for
, and by using
(2.6) for
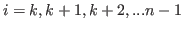 we get
we get
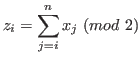 and
and
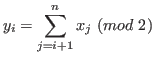 for
for
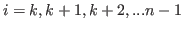 .
.
Clearly
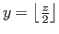 if and only if
if and only if 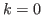 , and
, and
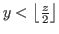 if and only if
if and only if 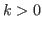 and
and
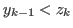 .
.
Therefore 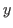 and
and 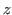 are determined by
are determined by 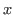 when we have (2.3) and (2.4).
In particular, for any
when we have (2.3) and (2.4).
In particular, for any 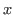 there exist unique
there exist unique 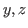 that satisfy (2.3) and (2.4).
that satisfy (2.3) and (2.4).
Theorem 2.2
If
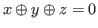 and
and
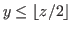 ,then
,then
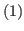
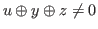 for any
for any
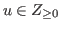 with
with 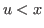 .
.
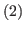
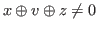 for any
for any
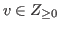 with
with 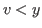 .
.
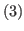
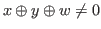 for any
for any
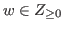 with
with 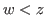 .
.
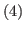
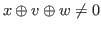 for any
for any
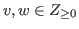 with
with 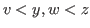 and
and
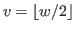 .
.
Lemma 2.4
For any
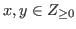 there exists
there exists 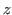 that satisfies one of the following two conditions.
that satisfies one of the following two conditions.
![$ [i]$](img152.png)
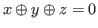 and
and
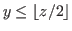 .
.
![$ [ii]$](img154.png)
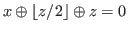 and
and
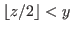 .
.
Theorem 2.3
Suppose that
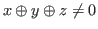 and
and
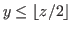 .
.
Then at least one of the following (1), (2), (3) and (4) is true.
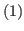
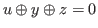 for some
for some
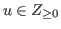 with
with 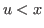 .
.
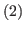
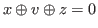 for some
for some
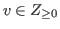 with
with 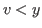 .
.
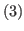
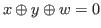 for some
for some
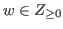 with
with 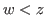 .
.
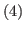
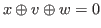 for some
for some
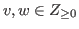 with
with 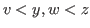 and
and
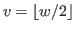 .
.
Definition 2.6
For
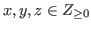 we define
we define
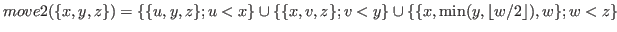 , where
, where
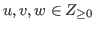 .
.
Theorem 2.6
Let
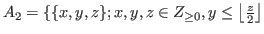 and
and
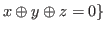 ,
,
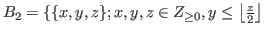 and
and
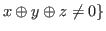 . Then
. Then
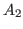 is the set of L-states and
is the set of L-states and 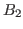 is the set of W-states of the game of Definition 2.4.
is the set of W-states of the game of Definition 2.4.
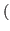 Note that
Note that 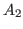 and
and 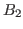 are defined in Definition 2.5.
are defined in Definition 2.5.
Proof
If we start the game with a state
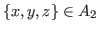 , then by Theorem 2.4 any option by us leads to a state
, then by Theorem 2.4 any option by us leads to a state 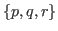 in
in  . From this state
. From this state 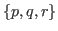 by Theorem 2.5 our opponent can choose a proper option that leads to a state in
by Theorem 2.5 our opponent can choose a proper option that leads to a state in 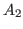 . Note that any option reduces some of the numbers in the coordinates. In this way our opponent can always reach a state in
. Note that any option reduces some of the numbers in the coordinates. In this way our opponent can always reach a state in 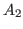 , and finally he wins by reaching
, and finally he wins by reaching
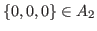 . Therefore
. Therefore 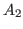 is the set of L-states.
is the set of L-states.
If we start the game with a state
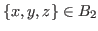 , then by Theorem 2.5 we can choose a proper option leads to a state
, then by Theorem 2.5 we can choose a proper option leads to a state 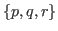 in
in 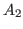 . From
. From 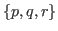 any option by our opponent leads to a state in
any option by our opponent leads to a state in 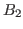 . In this way we win the game by reaching
. In this way we win the game by reaching
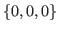 . Therefore
. Therefore 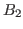 is the set of W-states.
is the set of W-states.
By Theorem 2.6 we tell L-states from W-states, and in Example 2.4 we learn how to win the game using the theorem.
Example 2.4
Here we present the method to win the chocolate game of Fig. 2.5. Since
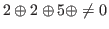 , by Theorem 2.6 the chocolate in Fig. 2.5 with the coordinates
, by Theorem 2.6 the chocolate in Fig. 2.5 with the coordinates 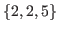 is a W-state. Therefore you can win if you play as the first player. The strategy is to move to an L-state every time. For example you can move to
is a W-state. Therefore you can win if you play as the first player. The strategy is to move to an L-state every time. For example you can move to 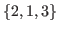 that is an L-state, since
that is an L-state, since
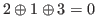 .
.
In this way you should leave the opponent with an L-state every time until you leave the opponent with the single block of bitter chocolate whose coordinates are 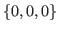 . Then the game is finished, and you win the game.
. Then the game is finished, and you win the game.
By Example 2.4 the strategy to win is clear. Even if you do not read the proof of Theorem 2.6, you can be a good player of this chocolate game.
Next: Chocolate games for k
Up: Abstract and the table of contents
Previous: Introduction
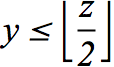 .
.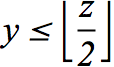 .
.
![\includegraphics[height=2.5cm]{choco1203b.eps}](img270.png)
 and
and
 with
with
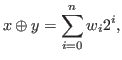
![\includegraphics[height=2.8cm]{choco1203b3.eps}](img52.png)
![\includegraphics[height=3.3cm]{choco1203b2.eps}](img53.png)
![]()
![]()
![]() and
and
![]() ,
,
![]() and
and
![]() .
.
![]() is the set of L-states and
is the set of L-states and ![]() is the set of W-states of the game of Definition 2.4.
To do this we need some lemmas and theorems.
In this section we assume that
is the set of W-states of the game of Definition 2.4.
To do this we need some lemmas and theorems.
In this section we assume that
![]() and we write them in base 2, so
and we write them in base 2, so
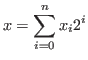 ,
,
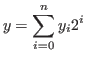 and
and
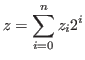 with
with
![]() , where
, where
![]() .
.
![]()
![]() if and only if
if and only if ![]() and
and
![]() for
for
![]() .
.
![]()
![]() if and only if
if and only if ![]() ,
,
![]() for
for
![]() and
and
![]() for some
for some
![]() .
.
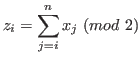 and
and
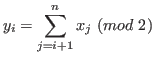 for
for
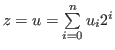 . By
. By 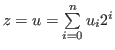 . By
. By 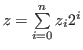 and
and
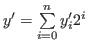 . Clearly
. Clearly
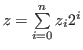 and
and
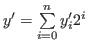 . Then
. Then
![]() using examples of states in Example 2.2 . If we start with the state
using examples of states in Example 2.2 . If we start with the state
![]() and reduce
and reduce ![]() to
to ![]() , then the second coordinate will be
, then the second coordinate will be
![]() .
.
![]() . It is easy to see that
. It is easy to see that
![]() . It is clear that
. It is clear that
![]() , since we cannot move to
, since we cannot move to ![]() from
from ![]() . Note that
. Note that
![]() , since it will take 2 steps to reach
, since it will take 2 steps to reach ![]() from
from ![]() .
.
![]() , then any move leads to an element of
, then any move leads to an element of ![]() .
.![]()
![]() , by
, by ![]() ,
, ![]() ,
, ![]() and
and ![]() of Theorem 2.3 there exists
of Theorem 2.3 there exists
![]() such that
such that
![]() . Therefore
. Therefore
![]()