Introduction

In this article we study new (bitter) chocolate games. A.C.Robin introduced a rectangle chocolate game in [1], but it was mathematically equivalent to the traditional game of nim.
There are other types of chocolate games, and one of the most well known is Chomp. Chomp is a game with a rectangular chocolate made up of smaller square blocks (rectangular cells). The players take turns, and they choose one block and eat it together with those that are below it and to its right. The top left block is very bitter and the players cannot eat this block. Although many people have studied this game, the winning strategy has not been discovered.
The authors have presented new chocolate games whose mathematical structures were different from that of traditional game of nim in [3], [8], [4] and [5]. The coordinates of the game in [4] satisfy the inequality 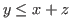$y \leq x+z$ , and the coordinates of the game in [5] satisfy the inequality 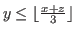$y \leq \lfloor \frac{x+z}{3} \rfloor$ , where 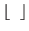$\lfloor \ \ \rfloor$ is the floor function. As to the coordinates 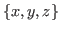$\{x,y,z\}$ of chocolate see Definition 2.4 of this article. These games are different from Chomp mathematically, and the winning strategy for them were discovered.
In [3] the authors presented many kinds of graphs produced by the set of L-states of the chocolate games.
In this article the authors present new chocolate games, and the coordinates 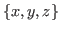$\{x,y,z\}$ of the chocolate satisfy the inequalities 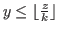$y\leq \lfloor \frac{z}{k} \rfloor$ for $k = 1,2$ .
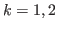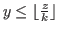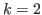In Section 2 we study the formula for the set of L-states and the winning strategy of the game with the inequality $y\leq \lfloor \frac{z}{k} \rfloor$ for $k = 2$ , and the formula for the set of L-states has been already presented in [6] and [8], but in this article the authors present proofs that are more simple and clearer than those in [6] and [8].
In Section 3 we define the chocolate game with the inequality 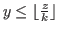$y\leq \lfloor \frac{z}{k} \rfloor$ for an arbitrary natural number 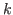$k$ , but we do not go into the detail of the theory.
In Section 4 we study Grundy number of the chocolate game with the inequality $y\leq \lfloor \frac{z}{2} \rfloor$ .
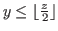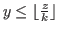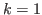In Section 5 we study the chocolate game that satisfies the inequality $y\leq \lfloor \frac{z}{k} \rfloor$ when $k = 1$ . This is a chocolate game without a simple formula for L-states. Here we use the table of Grundy number and its mathematical structure. The proofs for the case of 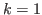$k = 1$ are presented in this article for the first time. The logic behind proofs is simple, but is is very difficult to present a complete proof.

In Section 6 we study beautiful graphs made by Grundy numbers of chocolate games of Section 2 and 5.

In Section 7 we study beautiful graphs made by Grundy numbers of chocolate games with two inequalities.