Next: Beautiful Graphs
Up:Abstract and the table of contents Previous: Case 4
Case 5
Next we study the case that 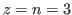
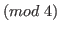 and
and 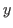 is odd.
is odd.
An example of this case is Example 5.6.
![\includegraphics[height=10cm]{tablenew2.eps}](img672.png)
In Fig. 5.23 we suppose that Predictions 5.1, 5.2, 5.3,5.4 and 5.5 are valid for
 and for
and for
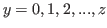 . We also suppose that these predictions are valid for
. We also suppose that these predictions are valid for 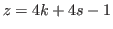 and
and
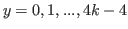 . Under these assumptions we prove that
. Under these assumptions we prove that
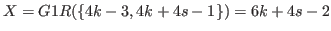 .
.
Remark 5.4
In this case we assume similar conditions that are written in Remark 5.3.
Note that some Grundy numbers
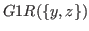 with
with
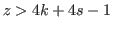 are presented in the table. We do not assume the values of these Grundy numbers to prove this prediction, but the authors present these numbers to show the relative positions of
are presented in the table. We do not assume the values of these Grundy numbers to prove this prediction, but the authors present these numbers to show the relative positions of
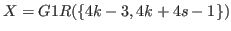 in the table of Grundy numbers.
in the table of Grundy numbers.
Here we assume that
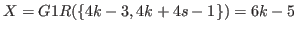 , which is the last number of the sequence
, which is the last number of the sequence
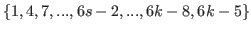 that is an arithmetic sequence with common difference of
that is an arithmetic sequence with common difference of 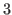 and its length is
and its length is
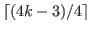 .
.
Therefore the position of
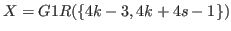 is in the midst of the the sequence
is in the midst of the the sequence
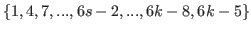 , and this condition make Case 5 very different from Case 1, Case 2 and Case 3.
, and this condition make Case 5 very different from Case 1, Case 2 and Case 3.
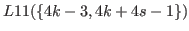
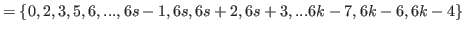
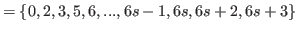 |
(5.61) |
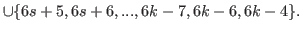 |
(5.62) |
Clearly
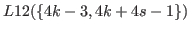
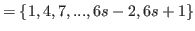 |
(5.63) |
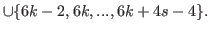 |
(5.64) |
By using Prediction 5.3 for 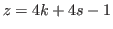 and
and
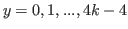
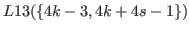
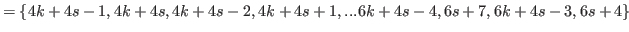
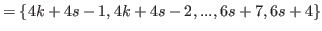 |
(5.65) |
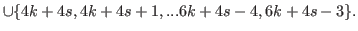 |
(5.66) |
By (5.61) and (5.63) we have
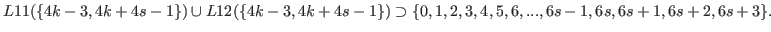 |
(5.67) |
By (5.62) and the fact that  we have
we have
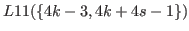
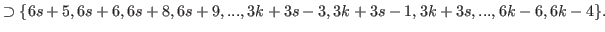 |
(5.68) |
By (5.65) and (5.66) we have
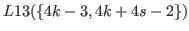
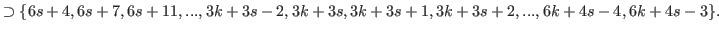 |
(5.69) |
By using predictions for 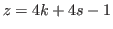 and
and
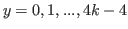
we know that the sequence of (5.69) starts as an arithmetic sequence with common difference of 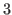 whose length is
whose length is
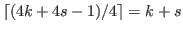 , and hence the last term of this arithmetic sequence is
, and hence the last term of this arithmetic sequence is
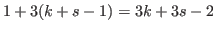 . The next term in (5.69) is
. The next term in (5.69) is 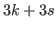 , and after that we have an arithmetic sequence with common difference of
, and after that we have an arithmetic sequence with common difference of 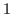 up until it reaches
up until it reaches 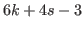 .
Therefore by (5.68), (5.67) and (5.69) we have
.
Therefore by (5.68), (5.67) and (5.69) we have
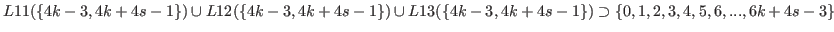 .
It is clear that there is no
.
It is clear that there is no 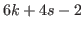 in
in
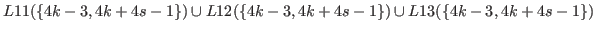 , and hence we have
, and hence we have
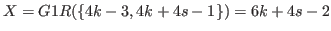 .
.
Proof
The outline of the proof is almost clear from Case 1, Case 2, Case 3, Case 4 and Case 5.
Theorem 5.1
The list of L-states of the game with inequality 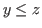 is the union of the following lists
is the union of the following lists 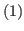 ,
, 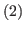 ,
, 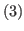 ,
, 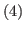 ,
, 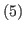 and
and 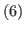 .
.
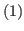 .
.
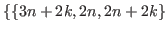 ,
,
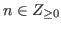 and
and 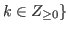
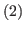 .
.
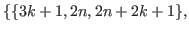
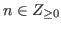 and
and 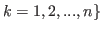
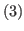 .
.
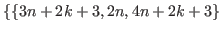 ,
,
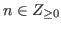
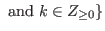
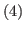 .
.
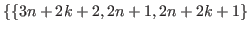 ,
,
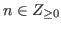 and
and 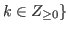
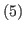 .
.
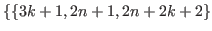 ,
,
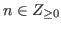 and
and 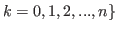
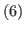 .
.
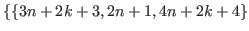 ,
,
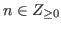 and
and 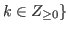 .
.
Proof
This is direct from Prediction 5.5.
Next: Beautiful Graphs
Up:Abstract and the table of contents Previous: Case 4
![\includegraphics[height=10cm]{tablenew2.eps}](img672.png)