Visual Magic Squares and Group Orbits I
1. Euler Squares and Their
Representations
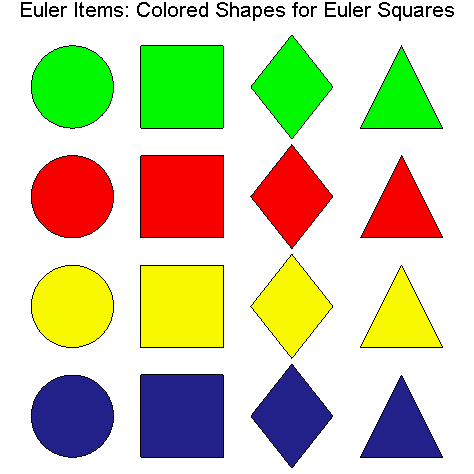
The colored shapes in the table below will be used to represent sixteen objects with each object having two visual attributes, color and shape. As indicated in the table, the color attribute takes on the four values: green, red, yellow, and blue; and the shape attribute takes on the four values: circle, square, diamond, and triangle.
Illustration
1.1
Definition 1.1. The collection of sixteen colored shapes in Illustration 1.1 will be called Euler items. A set of four Euler items is said to have the Euler property just in case each of the four values of the two attributes (color and shape) occur exactly once, i.e. none of the four Euler items can have the same color or shape. Notice that both the left and right main diagonals of the table in Illustration 1.1 have the Euler property, however none of the rows or columns have the Euler property, since the Euler items in each row all have the same color and the Euler items in each column all have the same shape. An Euler square is any rearrangement of the table above in which each of the four rows, the four columns, and the two (left and right) main diagonals have the Euler property.
In addition, we will refer to the process of creating Euler squares in pursuit of finding all Euler squares as the Euler game. Of course making one Euler square is a one person game or a solitaire, and such activities are often called puzzles.
Exercise 1.1. Play the Euler game by rearranging the Euler items (colored objects) in the table above until you have an Euler square. Here is an Euler items template that you can print out on photo quality paper and cut out to make your own pieces for the Euler game. Hint: Since both of the main diagonals in the table have the Euler property you can begin the game with either one of these diagonals, but not both (why?).
Exercise 1.2. Play the Euler game, making one Euler square of each of the following three diagonal types. Note that more than one answer (Euler square) is possible for each type.
Type D1. Start with the left main diagonal having the green circle at the top left and the blue triangle in the first position below the green circle on this diagonal. Complete to an Euler square.
Type D2. Start with the left main diagonal having the green circle at the top left and the blue triangle in the second position below the green circle on this diagonal. Complete to an Euler square.
Type D3. Start with the left main diagonal having the green circle at the top left and the blue triangle in the third position below the green circle on this diagonal. Complete to an Euler square. Note that you may have already done this in Exercise 1.1.
Exercise 1.3. Play the Euler game, making one Euler square of each of the following three row types. Note that more than one answer (Euler square) is possible for each type.
Type R1. Start with the top row having the green circle at the top left and the blue triangle in the first position to the right of the green circle on this row. Complete to an Euler square.
Type R2. Start with the top row having the green circle at the top left and the blue triangle in the second position to the right of the green circle on this row. Complete to an Euler square.
Type R3. Start with the top row having the green circle at the top left and the blue triangle in the third position to the right of the green circle on this row. Complete to an Euler square.
Definition 1.2. We want to numerically code Euler squares in order to aid us in their further study, classification, and generation. In order to do this, we must first numerically code our Euler items (colored shapes). So, let [c, s] be an ordered pair of integers from 0 to 3, then the different values of c = 0, 1, 2, 3 will represent green, red, yellow, and blue, respectively; and the different values of s = 0, 1, 2, 3 will represent circle, square, diamond, and triangle, respectively. This is the base 4 representation of our Euler items. In order to convert it to a base 10 representation, we simply set n = 4c + s.
The tables below illustrate this correspondence between our Euler items and their numerical coding in base 4 and base 10.
Base 4 and Base 10 Coding of Euler Items
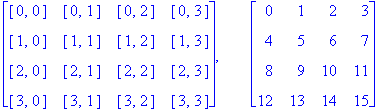
Illustration
1.2
If the Euler items in an Euler square are numerically coded using the base 4 (base 10) coding, the resultant numerical square will be called a base 4 (base 10) Euler square. For example, consider the following Euler square and its two numerical codings.
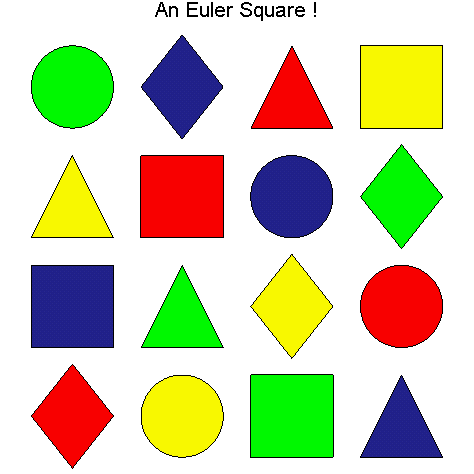
Base 4
and Base 10 Coding of this
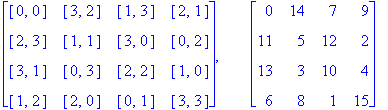
Illustration
1.3
Notice that the base 10 Euler square above is a (numerical) magic square, i.e. each row, column, and main diagonal sum to the same number, in this case 30. Of course, this is not an accident, since Euler squares were originally devised in order to present a visual and immediately accessible method for creating magic squares. Creating an Euler square using Euler items and then numerically coding it into a magic square is the simplest and most intuitive way we know for finding your first 4 ´ 4 magic square, and many more. This visual approach was presented in Singer [6], and the basic idea for the base 4 numerical coding dates back to a paper of Leonhard Euler [2] in which he demonstrates that one can obtain a magic square by adding certain pairs of (mutually) orthogonal Latin squares.
Definition 1.3. A 4´ 4 magic square is a 4 ´ 4 table of distinct integers (base 10) such that each row, column, and main diagonal all add up to the same magic sum (base 10 number). In this paper, we will use the integers from 0 to 15 and so our 4 ´ 4 magic squares will all have their magic sum equal to 30 (see Exercise 1.4).
Exercise 1.4. Investigate the last statement in Definition 1.3. Try to find a formula for the magic sum of a k ´ k magic square using the numbers from 1 to k2, and then adjust using the numbers from 0 to k2 - 1 instead. You might begin by doing this for k = 3 and then generalize. To this end, a fun preliminary exercise for k = 3 is to use the numbers from 1 to 9 to create a 3 ´ 3 magic square and see what the magic sum is.
Exercise 1.5. Recode each of the Euler squares found in Exercises 1.1-1.3 into their base 4 and base 10 representations, and then verify that the base 10 Euler squares are magic squares.
Theorem 1.4. Every base10 Euler square is a magic square.
Exercise 1.6. Try to explain why Theorem 1.4 holds by finding numerical properties of the base 4 coding of an Euler square that force the corresponding base 10 coding to be a magic square. Hint: Look carefully at your results in Exercise 1.5.
Notation. Below we will use vertical bars (absolute value sign) for the cardinality (size) of a set.
Definition 1.5. Let a be an Euler item and define a* to be the set of all complements of a, i.e. all Euler items b such that b differs from a in both attributes, namely color and shape. So, viewing the Euler items in Illustration 1.2 above, it is easy to see that for each item a, | a* | = 9, and further, if b Î a*, then | a* Ç b* | = 4.
Theorem 1.6. There are 1152 Euler squares.
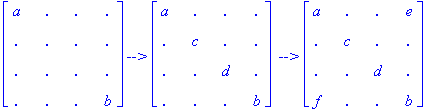
Exercise 1.7. Try to explain why Theorem 1.6 holds, using Definition 1.5 and the observations following it. Hint: Build an Euler square by first building the left main diagonal, starting with the first position on this diagonal, say a. Then select b in a* and place it in the fourth position on this diagonal. Now, you must use a* Ç b* to fill the remaining positions on this diagonal (why?). So, let a* Ç b* = {c, d, e, f} and keep going until all the remaining positions are forced, counting all the possible choices you had along the way. Here's a diagram indicating some of these steps:
Remark 1.7. Notice that we still have an Euler square if we apply any of the following eight symmetry transformation to an Euler square: rotation by 90, 180, 270, or 360 degrees about the center of the square; or a reflection in any of the following axes through the center of the square: horizontal, vertical, left main diagonal, or right main diagonal. In fact, our tally of Euler squares in Theorem 1.6 includes all those that may be obtained by applying these eight symmetry transformation to any Euler square already constructed. So, from the point of view of trying to construct and count all the essentially different Euler squares, we should divide 1152 by 8, yielding 144 essentially different Euler squares.