METHODS OF PERFECT COLORINGR. Pérez-Gómez 1andCeferino Ruiz 2
Keywords: Mosaic, Symmetry, Group, Tiling, Crystallographic Groups. 1 IntroductionAll the plane periodic mosaics may be classified by means of the determination of their symmetry group, having 17 different classes as a result [1], although from an artistic point of view their number may be infinite. However, if we bear in mind the colors, the number of groups which determine the symmetry of the mosaic is greater [10]. These groups are called chromatic groups. R.L.E. Schwarzenberger [8] contributed certain clarifications to the work of classifying chromatic compositions combining two monochromatic groups. This paper presents two methods of coloring monochromatic plane and
periodic mosaics by means of which color may be distributed making use
of the symmetry group associated to the monochromatic mosaic and its subgroups.
The main result is the Theorem where it is proved
that, when the subgroup used for the two colorings is normal, the coloring
result obtained is independent from the method used.
2 First Method of mosaic coloringLet G be the crystallographic group associated to a periodic tiling
T, and G1 one of its crystallographic subgroups
of index k. In these conditions, the union of basic, suitable,
k
tiles for G define a basic tile for G1.
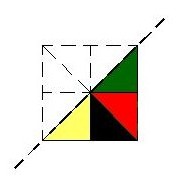
Method 1 (M1)With k colors available, a basic tile for G1 is colored by assigning a color to each of the k basic tiles of the tiling T (which has been primarily determined). The coloration is then extended over the whole tiling by the action of group G1 on the basic tile. This form of coloring has the definition of the color stains, which we will deal with in a forthcoming article [3], and of the classes giG1 and G1gi, with i = 1,2,¼,k, to the left and to the right respectively. If G1 is a normal subgroup in G, both classes coincide. In another case we will see that the colorings which can be obtained are less fine such as will be shown in the following example. Example 1 Let G be the group of the type p4m associated to a pattern of squares which tiles the plane. Taking the translations T, and the reflection sL from the G group represented in Figure 1, we form T È{sL} and we take this as a set of generators of the subgroup G1 which proves to be of the cm type. G1 is not normal in G, as if we take a rotation of G, for example, rC,p/2, we have that:
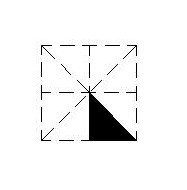
Figure 1: Basic tile for G. Figure 2: 1st Basic tile for G1.
Figure 3: Colored by the action of G1 on the 1st basic tile. Proposition 1 Let G1 be a crystallographic subgroup of G of index k. Let KG be a basic tile for G and KG1 a basic tile for G1 obtained by uniting k tiles giKG, i = 1,2,¼,k, with giÎ G and giG1¹ gjG1 if gi ¹ gj. The resulting coloring when applying M1 to the tiling TG = {gKG; g Î G} from KG1 does not depend on KG1. Proof: Let KG1 and LG1 be two basic different G1 tiles, obtained by uniting giKG, i = 1,2,¼,k and giÎG, and [`g]sKG, s = 1,2,¼,k and [`g]sÎG, respectively. For each giKG a g1Î G exists such that g1(giKG) ÍLG1, therefore a unique [`g]s exists such that g1(giKG) = [`g]sKG. Later g1gi = [`g]s and g1 = [`g]sg-1i. The permutation of colors which takes the color from giKG in that of [`g]sKG permutes the TG tile colors, colored by M1 starting from KG1, in the colors obtained from LG1. In fact, any tile obtained starting from giKG by the action of G1 will have the type h1(giKG). As h1 Î G1, m = h1(g1)-1 ÎG1 and h1 = mg1. Then, h1(giKG) = mg1(giKG) = m(g1giKG) = m([`g]sKG). With the tiles giKG and [`g]sKG having the same color as h1(giKG) and m([`g]sKG), the permutation which takes the color from giKG to that of [`g]sKG also takes that of h1(giKG) to that of m([`g]sKG). 
Figure 4: 2nd basic tile. Coloring by G1 If we change subgroup, logically, other results are obtained if the G1 index is maintained in G like the basic G tile, see Figure 5 in which a subgroup of the p1m1 type has been used. Figure 5. Definition 1 Let a periodic tiling be of R2, in which each tile is colored with a color from among k possible colors. According to Senechal [9] we will say that k-coloring is perfect or compatible if each symmetry of the periodical mosaic discoloring induces a permutation of the k colors. This type of coloring makes all the tiles which have the same color (for example, red) be transformed by means of a symmetry of the discolored periodical mosaic in tiles of the same color (for example, blue); symmetries of the discolored periodical mosaic do not exist which may mix colors in the meaning of transforming, for example, some red tiles in blue and others, also red, in green. Proposition 2 The coloring done by M1 is perfect if and only if G1 is normal in G. Proof: Let us call Gi the set of elements of G which stabilize the color i :
(Note: By means of g(i) = j we want to express that all basic tiles for G colored in the i color passes by means of the element g to another of the j color). It is evident that G1 ÍGi. Let us see if the other inclusion is fulfilled. Let Ki be an i colored tile. g1ÎG1 and K exist, and they are unique. Taking gÎGi we have a Ki¢ tile, Ki¢ = gKi = gg1K, of i-color. Then gg1ÎG1 from where gÎG1. Now, let Ki be a basic i colored tile for G, Ki = g1K. We will obtain another basic tile for G of j color applying any g of G to Ki : gKi = gg1K. On the other hand, g1¢ÎG1 and Kj, will exist and they are unique, first basic tile for G of j color, such that:
Let Ki¢ be another basic tile for G of color i:
3 Second Method of mosaic coloringMethod 2 (M2)The symmetries of G1 act upon a chasen basic tile, for G, which is painted with a determined color (for example, yellow) and all its images because of the action of G1 will have its the same color. Each one of the classes on the left hand side of G1 in G will be identified with one of the available k colors and the symmetries of such a class are utilized to transform the original tile (in our example, black) into tiles which have the color assigned to such a class. In this way, the tiling remains painted with k colors. Example 2 If M2 is applied to the basic tile
for G of Figure 1, and we take the same
generators for G1 - that is, sL
and T- the resulting coloring is the same that of Figure
4.
Proof: We can see that the technique utilized guarantees that it is a perfect k-coloring. Let the K¢ and K¢¢ tiles be of the same color. g¢ and g¢¢ of G, exist, belonging to the same class, g¢G1 = g¢¢G1, and the basic tile for G, K, to color in such a way that:
Let g be any element of G:
later gK¢ and gK¢¢ has the same color (that corresponding to the gg¢G1 class). As a consequence, g induces a permutation of colors. Proposition 4 The correspondence which is established on coloring according to M2 between the elements of G and the group of permutations of k colors, Sk, is a homomorphism of groups. Proof: Taking left hand side classes a homomorphism can be defined between G and the group of the permutations of k elements Sk with the composition. In effect, representing the quotient G/G1 by
The application p: g Î
G ® p(g), where
p(g)
Î
Sk is the matrix
is a homomorphism. In effect:
In this homomorphism, used in the previous demonstration, we can verify that Ker p Í Çi = 1k Gi = G1, Gi being the stabilizer of i color, that is, fixed an i, Gi = {gÎG; ghiG1 = hiG1}. Each one of the subgroups Gi is a class of conjugation of G1. Remark 1 A permutation of the K colors is associated to each element of G. That is, all symmetry operations have an element of the group of permutations of order k, Sk associated. Besides, as the product of symmetries is corresponded to the composition of permutations, we have seen that the nucleus of the homomorphism p: G ® Sk is formed by all the symmetries which leave all the colors invariant because it is associated to the permutation identity. The knowledge of G/Ker p is useful for being isomorphous to p(G), but it has the problem that knowing Ker p we know nothing about the permutation, p(g), which corresponds to any g. Therefore we have to substitute Ker p for a subgroup G1, Ker p Í G1, by means of which one unique color remains invariant. In the particular case in which G1 = Ker p, it will be necessarily normal and the classes will coincide on the right and on the left. Remark 2 In the demonstration of the Proposition 3 we have taken classes from the left. We make this obsevation because it is not the same to take classes from one side as from the other. Only in the case of G1 being normal will the results coincide; this happens in the bi-color symmetry when k = 2. Remark 3 One color is assigned to each class on the left, in this way the action of the elements of that class transform the assigned color to the G1 class in it. Therefore, we can write G as finite union classes on the left, G = G1Èh1G1ȼÈhk-1G1. Remark 4 We believe we contribute a different method to obtain perfect k-colorings on those noted in Senechal [9] and before, giving an interpretation of their mathematical significance. Corollary 1 If a tiling is colored by the action of a G group and one of its subgroups G1 according to M2, the number of colors coincides with the index of G1 in G. 4 Relationship between the two MethodsTheorem 1 If the subgroup G1 is normal in G, the obtained colorings for M1 and M2 coincide.Proof: It is deduced from above-mentioned results and that, in this case:
Definition 2 Let us call a chromatic group, with k colors, the trio (G,G1,f ) where
Remark 6 The subgroup G1 = ÇgÎG gG1g-1, complete intersection of the conjugation family of G1, is a normal and crystallographic subgroup of G. Besides, G1 = Ker f. Remark 7 The homomorphism f: G ® Sk induces a monomorphism:
References:
Rafael Pérez-Gómez Dpt. Matemática Aplicada, EU Arquitectura Técnica, Univ. Granada, 18071 - Granada, Spain. e-mail: rperez@ugr.es Ceferino Ruiz
1991 Mathematical Subject Classification. Primary 20H15; Secondary 52C20. 1) Research partially supported by a Research Group in Applied Mathematics grant FQM-0191 2) Research partially supported by a DGICYT grant PB97-0785 and Research Group in Geometry grant FQM-0203
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||