Regular polyhedrons are formed by regular polygons, which are congruent. There are only five regular polygons, i.e. the Platonic solids:

· the tetrahedron consisting of four equilateral triangles

· the hexahedron (cube) consisting of six squares

· the octahedron consisting of eight equilateral triangles

· the dodecahedron consisting of twelve equilateral pentagons

· the icosahedron consisting of twenty equilateral triangles.

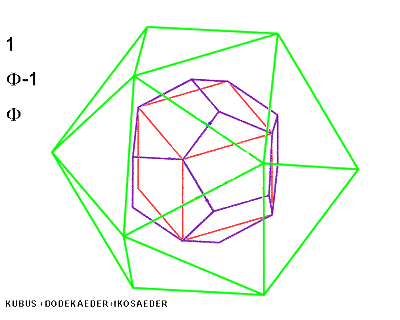
The five Platonic solids are combined in the Metaeder so that, complementary to each other, the packable (i.e. space-filling without any gaps) tetrahedrons and octahedrons are inscribed within a cube, and the not space-filling dodecahedrons and icosahedrons are circumscribed.

In this way, I make a difference between the intracubical and the extracubical polyhedrons. In the Metaeder, we thus find a large number of stringent parametric relations; if, as consistent throughout this study, the lengths of the sides of a cube are considered equal to 1, the length of the side of a tetrahedron is Ö2, of the octahedron ½ Ö2, of the dodecahedron 1/j and of the icosahedron j.

The intracubically packable Platonic solids thus follow the sequence ½ Ö2 : 1 : Ö2 : 2 etc. with the factor of Ö2 (as with the German Industrial Standard, i.e. DIN format), the extracubic solids following the harmonic sequence 1/j : 1 : j : j² etc. with the factor j. The number 1 as edge length of the cube is common to both progressive series. The spatial diagonal Ö3 of the cube has been introduced in addition to this.

PLATONIC SOLIDS