 |
||
 |
||
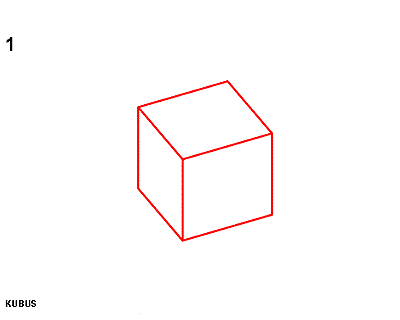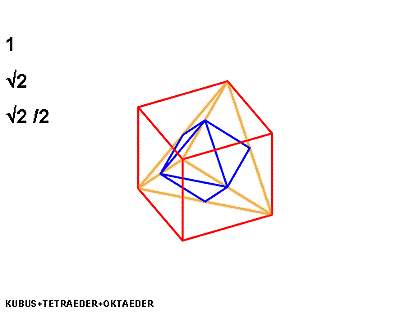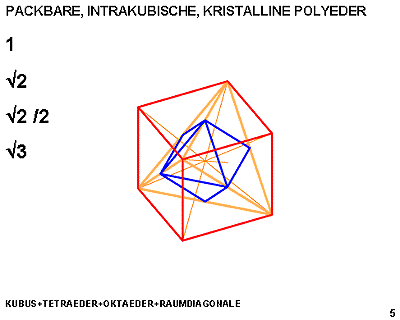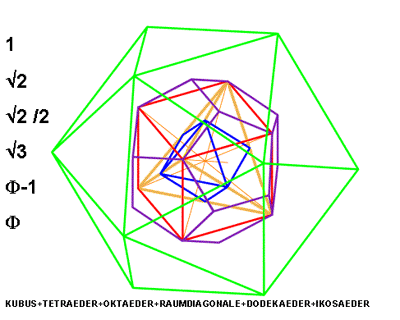
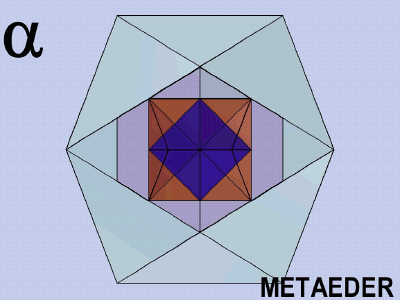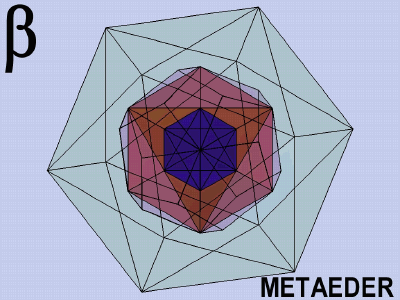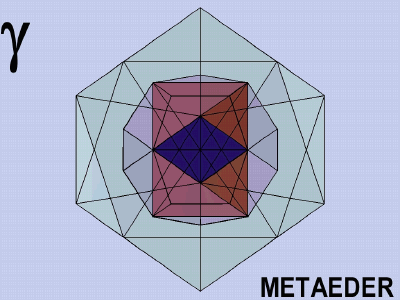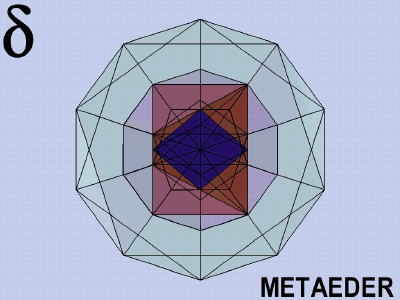
The Metaeder contains:
The universality of the Metaeder is the theoretical basis of structural architecture, inasmuch as it consists of equal, or similar or different, but coordinated elements. It contains the elementary cells of a structural architecture, it provides the sum of possibilities of regular space divisions.
The Metaeder is an object of meditation, a spatial mandala; its laws, proportions and beauties are revealed only in the spatial model.