GOLDEN SECTION IN METAEDER

The golden section is the ratio between two portions of a line, or the two dimensions of a plane figure, in which the lesser of the two is to the greater as the greater is to the sum of both. The portions and their sum are described by the equation F = 1.618 or the ratio of approximately 0.618 to 1. This gives a harmonic series, which is additive and geometric at the same time, i.e. the sum or product of two successive values in the series provide the next value. This is the only series having this remarkable property, and forms a basis for growth mechanisms in living organisms.

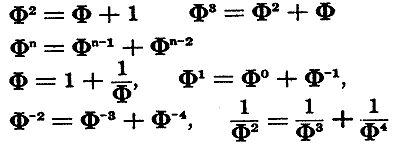
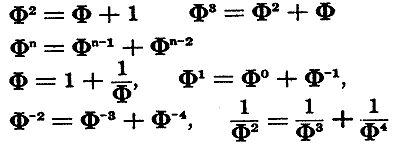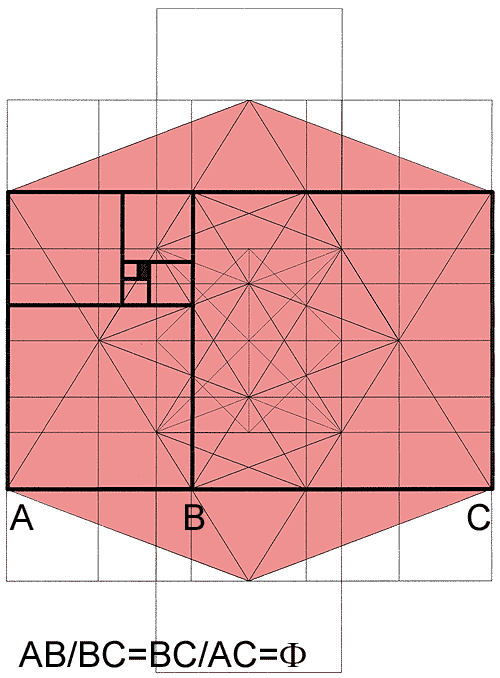
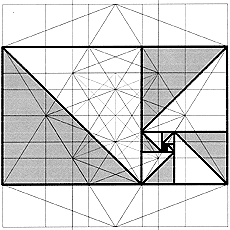
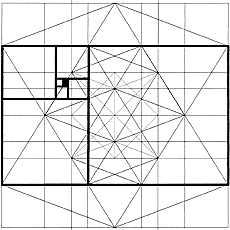
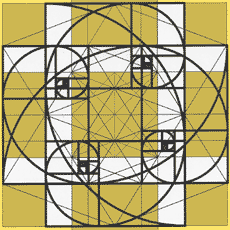
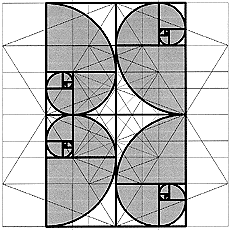
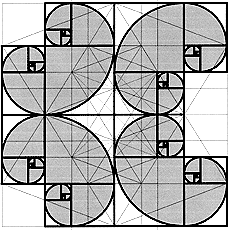
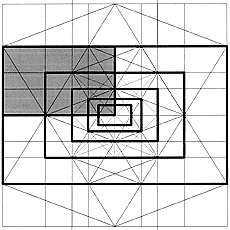
If a square is added to one of the longer sides of a harmonic rectangle having a side-to-side ratio F, a further harmonic rectangle with size ratio F is obtained. The square is the gnomon of the harmonic rectangle, defined as the smallest area added to a defined surface generating a surface similar to it.

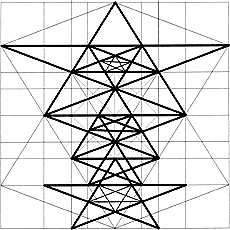
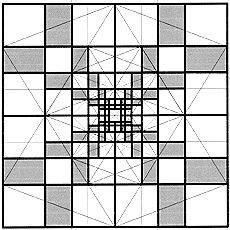
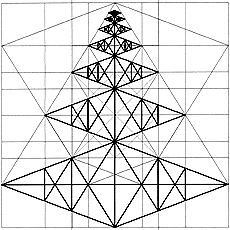
The continuous addition of squares to a golden rectangle generates the spiral arrangement of self-similar squares and the harmonic spiral.

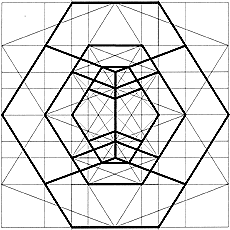
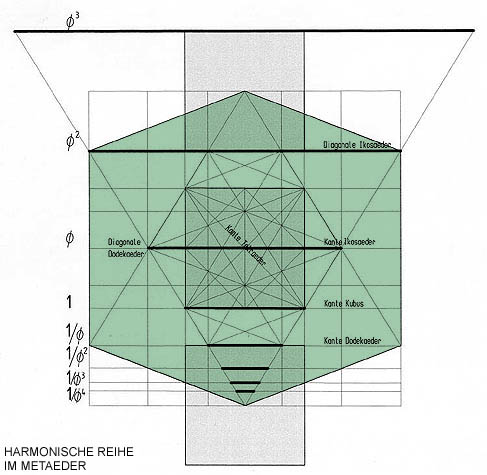
Die diagonal surface in the icosahedron is a harmonic rectangle, in which the harmonic spir al is contained, with its self-similarity so to speak a historic fractal. It is contained in the Metaeder.

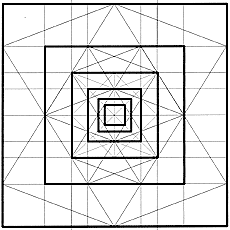
From my subjective viewpoint, the progressive series and the spiral constitute the "junction" between Euclidean and fractal geometry.