





... 1/j³ : 1/j² : 1/j : 1 : j : j² : j³...
(In additive progression, each value is the sum of the two preceding ones. These properties produce an arithmetical and geometrical series at the same time.)
But it is also based on the additive Fibonacci number series, i.e.:
1 : 1 : 2 : 3 : 5 : 8 : 13 : 21 : 34 : 55 : 89 ...
in which each value is the sum of the two preceding ones, an approximation to the harmonic series, and thus tends rapidly to j, as shown by:
2 - 1,5 - 1,6 - 1,625 - 1,6154 - 1,619 - 1,6176 - 1,6181 - 1,6179 > j= 1,6180339
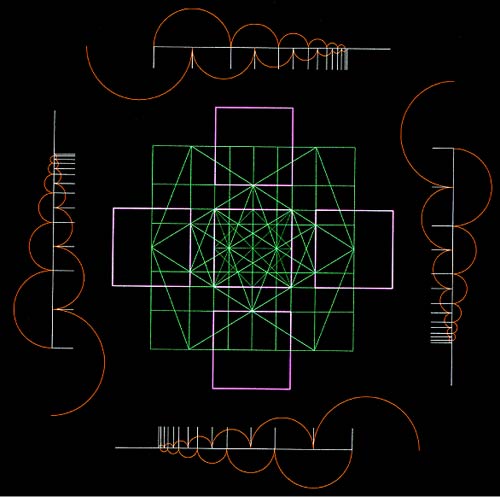
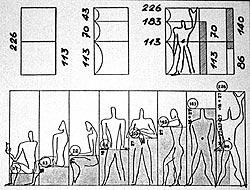
10 - 16 - 27 - 43 - 70 - 113 - 183 - 296 (red series)
and its doubling:
20 - 33 - 53 - 86 - 140 - 226 - 366 - 592 (blue series)
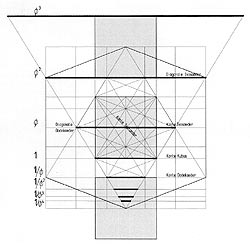
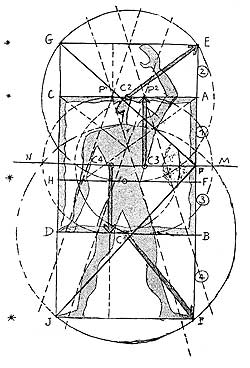
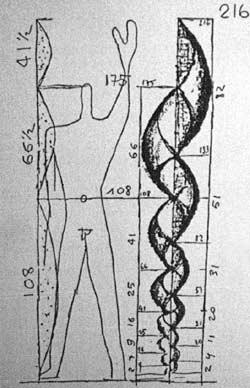
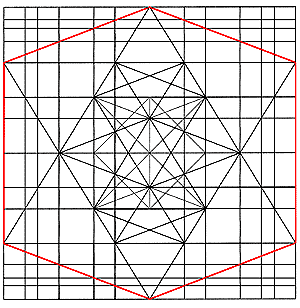
The harmonic series is contained in the Metaeder. The Modulor is situated on a.
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||